线性回归目的是找到一条直线（或者超平面）尽可能地接近所有的训练数据点，而对数几率回归的目的是找到一条直线（或者超平面）尽可能地分开两种不同类别的数据点。

对数几率回归感觉更像是一个分类问题。https://blog.csdn.net/amds123/article/details/70243497这篇博客中·已经讲的很好了，分类问题的结果是0或1。而对于logistic回归，我们不再要求直接给出分类结果，而是通过要求“分类结果为1的概率”进而得到分类结果，而概率属于[0,1]。

下面就看下公式的推导。按照sigmoid函数的形式作为正类的概率。下面是sigmoid函数

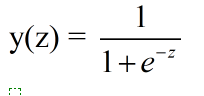
这个函数的图像是这样的

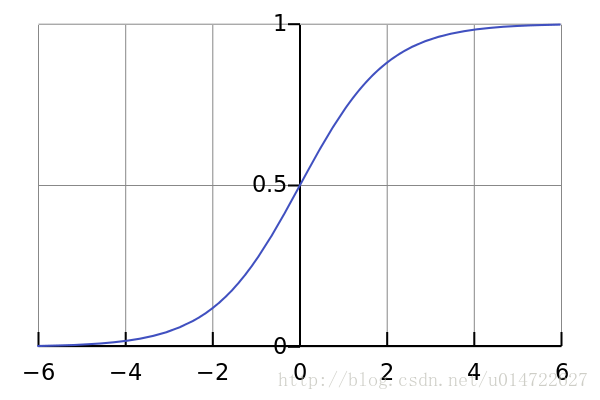
接下来我们只要做出广义上的线性回归，

接下来的我们可以从最大熵模型中推导，最大熵模型为

对于二分类问题

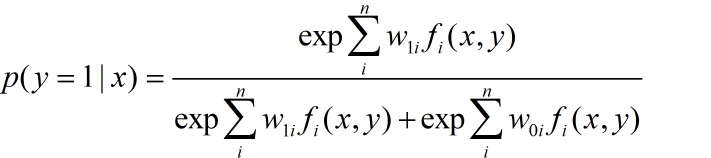
上下同除分子，再另wi  = w1i - w0i就可以得到下面的式子

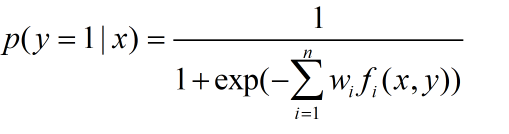
这样正类的概率为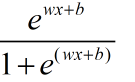，反类的概率为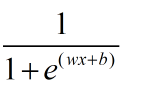这里我们可以令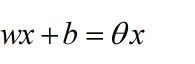，遵从伯努利分布，我们可以得到概率分布函数

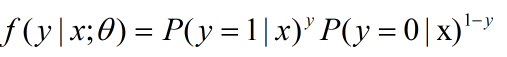
用极大似然估计法得到似然函数

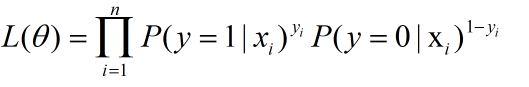
取对数就可以得到：

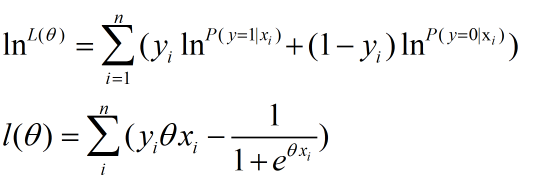
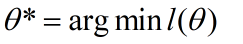
接下来我们可以用梯度下降法求出合适的值

logisitic回归的更多相关文章

  1. 【Machine Learning in Action --5】逻辑回归（LogisticRegression）

    1.概述 Logistic regression(逻辑回归)是当前业界比较常用的机器学习方法,用于估计某种事物的可能性. 在经典之作<数学之美>中也看到了它用于广告预测,也就是根据某广告被 ...

  2. logistic回归梯度上升优化算法

    # Author Qian Chenglong from numpy import * from numpy.ma import arange def loadDataSet(): dataMat = ...

  3. Python爱好者社区历史文章列表（每周append更新一次）

    2月22日更新:   0.Python从零开始系列连载: Python从零开始系列连载(1)——安装环境 Python从零开始系列连载(2)——jupyter的常用操作 Python从零开始系列连载( ...

  4. [DeeplearningAI笔记]序列模型2.7负采样Negative sampling

    5.2自然语言处理 觉得有用的话,欢迎一起讨论相互学习~Follow Me 2.7 负采样 Negative sampling Mikolov T, Sutskever I, Chen K, et a ...

  5. 浅谈Logistic回归及过拟合

    判断学习速率是否合适?每步都下降即可.这篇先不整理吧... 这节学习的是逻辑回归(Logistic Regression),也算进入了比较正统的机器学习算法.啥叫正统呢?我概念里面机器学习算法一般是这 ...

  6. Stanford机器学习---第三讲. 逻辑回归和过拟合问题的解决 logistic Regression & Regularization

    原文:http://blog.csdn.net/abcjennifer/article/details/7716281 本栏目(Machine learning)包括单参数的线性回归.多参数的线性回归 ...

  7. 【Coursera】线性回归和逻辑回归

    一.线性回归 1.批量梯度下降法 每次对参数进行一次迭代时,都要扫描一遍输入全集 算法可以收敛到局部最优值 当迭代多次之后,每次迭代参数的改变越小 2.随机梯度下降法 对于一个输入样本,对参数进行一次 ...

  8. 神经网络、logistic回归等分类算法简单实现

    最近在github上看到一个很有趣的项目,通过文本训练可以让计算机写出特定风格的文章,有人就专门写了一个小项目生成汪峰风格的歌词.看完后有一些自己的小想法,也想做一个玩儿一玩儿.用到的原理是深度学习里 ...

  9. SVM分类与回归

    SVM(支撑向量机模型)是二(多)分类问题中经常使用的方法,思想比较简单,但是具体实现与求解细节对工程人员来说比较复杂,如需了解SVM的入门知识和中级进阶可点此下载.本文从应用的角度出发,使用Libs ...

随机推荐

  1. Nlog日志出坑合集

    .net core框架下nlog不记录: 1.安装NLog.Web.AspNetCore 2.在Startup.cs文件的方法public void Configure(IApplicationBui ...

  2. OGG故障集锦（一）

    说明:此系列仅作OGG故障记录,未包含处理过程.仅作故障备案 ①   ERROR OGG-00519 Source Context : SourceModule : [ggapp.ddl] Sourc ...

  3. python 基于Anaconda import numpy 报错 Importing the multiarray numpy extension module failed.

    在windows中安装了 Anaconda 运行时报错 原因是系统环境变量起初并没有引入 E:\Tools\Anaconda\Library\bin 解决办法: 在系统环境变量中加入    E:\To ...

  4. ThinkPHP5.1完全开发手册.CHM离线版下载

    ThinkPHP5.1完全开发手册.CHM离线版下载 ThinkPHP5.1完全开发手册离线版.CHM下载地址 百度云:链接: https://pan.baidu.com/s/1b4jKJN-8UyI ...

  5. php ecshop 二级域名切换跳转时session不同步，解决session无法共享同步导致无法登陆或者无法退出的问题

    echshop基础上做了单点登录的 一级域名与二级域名 退出时 清空session 都是一级域名的session 因为二级域名的session是设置在二级域名上的 echshop基础上没有做单点登录的 ...

  6. Order Helper

    using System; using Microsoft.Xrm.Sdk; using Microsoft.Xrm.Sdk.Query; using Microsoft.Crm.Sdk.Messag ...

  7. 7z 压缩解压简单示例

    7z命令行压缩示例: 7z -tZip a test.zip ./test/* -mx0 把test文件夹中所有文件以存储压缩的模式压缩成zip格式的文件,压缩文件为test.zip a为添加选项   ...

  8. vowels_单元音

    vowels(美式): 单元音: [i]:需要用劲喊出类似于“yi”的四声,费力咧开嘴,单词eat.need.thief.meet. [?]:卷舌音,单词bird.her.worry.certain. ...

  9. Python学习笔记五：字符串常用操作，字典，三级菜单实例

    字符串常用操作 7月19日,7月20日 ,7月22日,7月29日,8月29日,2月29日 首字母大写:a_str.capitalize() 统计字符串个数:a_str.count(“x”) 输出字符, ...

  10. python类的多态

    1. 什么是多态     多态指的是同一种/类事物的不同形态   2. 为何要用多态     多态性:在多态的背景下,可以在不用考虑对象具体类型的前提下而直接使用对象     多态性的精髓:统一   ...