【Machine Learning】如何处理机器学习中的非均衡数据集？

在机器学习中，我们常常会遇到不均衡的数据集。比如癌症数据集中，癌症样本的数量可能远少于非癌症样本的数量；在银行的信用数据集中，按期还款的客户数量可能远大于违约客户的样本数量。

比如非常有名的德国信用数据集，正负样本的分类就不是很均衡：

如果不做任何处理简单地进行训练，那么训练结果中（以SVM为例），大部分好客户（约97%）能被正确地识别为好客户，但是大部分的坏客户（约95%）却会被识别为好客户。这个时候，如果我们仅仅使用accuracy来评价模型，那么银行可能会承受违约带来的巨大损失。在南大周志华老师的《机器学习》“模型的选择与评价”部分中，就提到了使用Precision、Recall、F1 Score(加权平均Precision和Recall)等更全面评价模型的方法。本文将探讨如何解决机器学习中遇到的分类非均衡问题：

过采样 Over-sampling
下采样 Under-sampling
上采样与下采样结合
集成采样 Ensemble sampling
代价敏感学习 Cost-Sensitive Learning

注：github开源项目github-scikit-learn-contrib/imbalanced-learn中提供了本回答中大部分算法的实现代码，并配有详细的文档和注释。

过采样 Over-sampling

过采样即是将本来数量少的那类样本增加。目前比较常见的方法包含了SMOTE, ADASYN, SVM SMOTE,bSMOTE。其中，SMOTE和ADASYN算法的实现也可以参考这个github项目。

我可视化了一下结果：比如说在下图中，蓝色三角形代表的是多数样本(不妨设为正例)，绿色三角形代表的是原始的少数样本(不妨设为反例)，而红色圆点则是使用SMOTE算法生成的反例。

类似地，ADASYN也可以有类似的效果。

不过，SMOTE在一些情况下表现得并不是特别好，也不是很稳定，这也与它本身的算法思路有关。我们可以对比一下在下面情况下SMOTE和ADASYN的表现：

但ADASYN也不是完美无缺的——当分割两个类别样本能够清晰地被划分而且数据点间隔很大时ADASYN会出现NaN。例如在以下的情况，ADASYN就很可能会出问题：

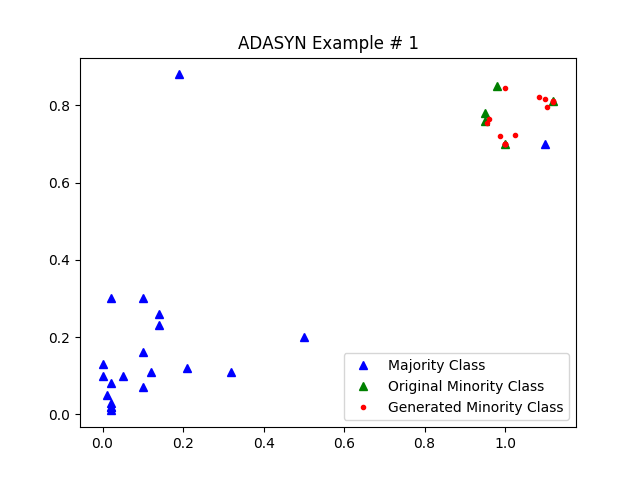
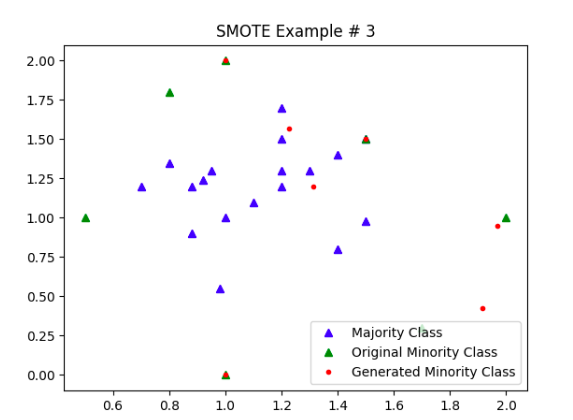
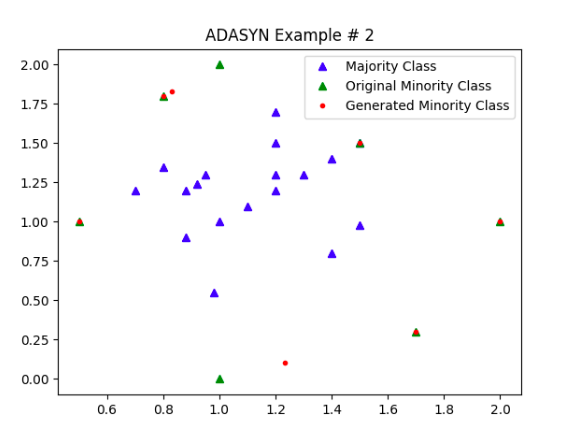
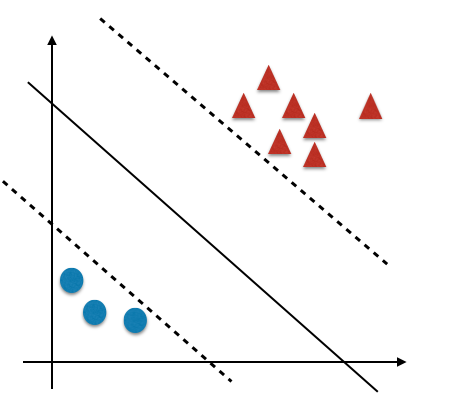
SMOTE：SMOTE: Synthetic Minority Over-sampling Technique

ADASYN：ADASYN: Adaptive Synthetic Sampling Approach for Imbalanced Learning

下采样 Under-sampling

下采样即是将本来数量多的那类样本减少。随机下采样就不用说了，实现非常简单。但它的表现并不是很好，因此又有了一些新方法，比较知名的有：

Tomek links
One-sided selection: Addressing the curse of imbalanced training sets: One-sided selection
Neighboorhood Cleaning Rule: Improving identification of difficult small classes by balancing class distribution
NearMiss: kNN approach to unbalanced data distributions: A case study involving information extraction

上采样与下采样结合

顾名思义，将原本比较多的样本所属类别的样本减少，同时也将原本属于少数的样本类别中的样本增加。

集成采样 Ensemble sampling

如我们所知，一些下采样的方法可能会使我们丢失一些比较重要的数据点，但是Xu-Ying Liu, Jianxin Wu, and Zhi-Hua Zhou的论文Exploratory Undersampling for Class-Imbalance Learning中提出了EasyEnsemble和BalanceCascade的方法一定程度上解决了这个问题。

在论文中，作者提到，EasyEnsemble的思想有一部分与Balanced Random Forests相似，但是EasyEnsemble使用了样本来随机训练决策树。

代价敏感学习 Cost-Sensitive Learning

我们都知道比起将一个正常客户误判为不良贷款客户，将一个不良贷款客户误判为正常客户可能会给银行带来更大的损失；比起将非癌症病人误判为癌症病人，将癌症病人误判为非癌症病人可能会导致治疗无法及时进行从而导致更严重的后果。于是就有了cost-sensitive learning这样的思路——来解决这种样本分类不均衡的问题。这部分可以参考Charles X. Ling, Victor S. Sheng的论文Cost-Sensitive Learning and the Class Imbalance Problem：