SGU - 282

SGU - 282

题解

题意：

本质不同的集合：不存在两个方案重新编号之后对应的边集相同（对于所有x,y,，(x,y)边颜色都相同）。

(1≤ N≤ 53, 1≤ M≤ 1000)

对P取模

本质不同，想到置换

置换在哪里？

就是重新编号

本质是一个n!大小的置换群

不能枚举每一个置换了，考虑对相同的置换一起处理

置换之后也要找环，所以直接枚举环的情况，处理对应这种环的组合的置换的出现次数，再处理环的组合的不动点

自然数拆分出环

环长为li，有k个，对应置换个数：

如果每一个都不同:$\frac{n!}{(l1!*l2!..lk!)}*((l1-1)!)*((l2-1)!)*((lk-1)!)$

如果

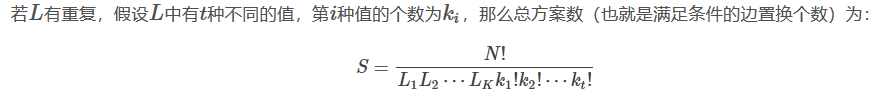
就是分配环的所属的时候，大小相同的环都是相同的。

所以再进行一次多重集合的排列。

每个置换的不动点个数：

考虑环自己内部连边的“环”个数：$1+\lfloor \frac{l-2}{2} \rfloor$

证明考虑边上相隔1一定一种，相隔若干会连出一些，手画几个

2->1

3->1

4->2

5->2

6->3

7->3

环与环之间的连边的“环”个数：$gcd(l1,l2)$

一个连边的颜色，会走$lcm(l1,l2)$才会重复，

期间l1的每个点连出去了lcm(l1,l2)/l1=l2/gcd(l1,l2)

一共连出去l2个点，每确定一个颜色就确定了l2/gcd(l1,l2)个颜色，所以共有gcd(l1,l2)个“环”

环总数tot

每个环m种颜色，m^tot即可。

1.自然数拆分+计算对应置换个数->枚举所有置换

2.每个自然数拆分计算不动点个数+再乘上对应置换个数->处理所有不动点

完毕。