Codeforces Round #527 (Div. 3) F. Tree with Maximum Cost 【DFS换根 || 树形dp】

传送门：http://codeforces.com/contest/1092/problem/F

F. Tree with Maximum Cost

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

You are given a tree consisting exactly of nn vertices. Tree is a connected undirected graph with n−1n−1 edges. Each vertex vv of this tree has a value avav assigned to it.

Let dist(x,y)dist(x,y) be the distance between the vertices xx and yy. The distance between the vertices is the number of edges on the simple path between them.

Let's define the cost of the tree as the following value: firstly, let's fix some vertex of the tree. Let it be vv. Then the cost of the tree is ∑i=1ndist(i,v)⋅ai∑i=1ndist(i,v)⋅ai.

Your task is to calculate the maximum possible cost of the tree if you can choose vv arbitrarily.

Input

The first line contains one integer nn, the number of vertices in the tree (1≤n≤2⋅1051≤n≤2⋅105).

The second line of the input contains nn integers a1,a2,…,ana1,a2,…,an (1≤ai≤2⋅1051≤ai≤2⋅105), where aiai is the value of the vertex ii.

Each of the next n−1n−1 lines describes an edge of the tree. Edge ii is denoted by two integers uiui and vivi, the labels of vertices it connects (1≤ui,vi≤n1≤ui,vi≤n, ui≠viui≠vi).

It is guaranteed that the given edges form a tree.

Output

Print one integer — the maximum possible cost of the tree if you can choose any vertex as vv.

Examples

input

Copy

8
9 4 1 7 10 1 6 5
1 2
2 3
1 4
1 5
5 6
5 7
5 8

output

Copy

121

input

Copy

1
1337

output

Copy

0

Note

Picture corresponding to the first example: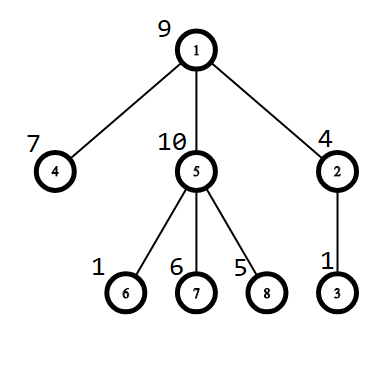

You can choose the vertex 33 as a root, then the answer will be 2⋅9+1⋅4+0⋅1+3⋅7+3⋅10+4⋅1+4⋅6+4⋅5=18+4+0+21+30+4+24+20=1212⋅9+1⋅4+0⋅1+3⋅7+3⋅10+4⋅1+4⋅6+4⋅5=18+4+0+21+30+4+24+20=121.

In the second example tree consists only of one vertex so the answer is always 00.

题意概括:

给出一棵 有 N 个结点 N-1 条边的树，每个结点的权值为 a[ i ], 每条边的边权为 1 .

每一点的贡献 = 该点的深度 * 该点的权值。

所以以不同的点作为 整棵树的根 会得到不同的树结点的贡献总和。

求最大的树结点的贡献组合。

解题思路：

一、树的换根 两次DFS

跑第一次DFS，处理出 Sum[ u ] 以 u 为根的子树的贡献总和（包括 u 结点本身），处理出以 结点1为根 的树的贡献总和 res；

第二次 DFS 换根：

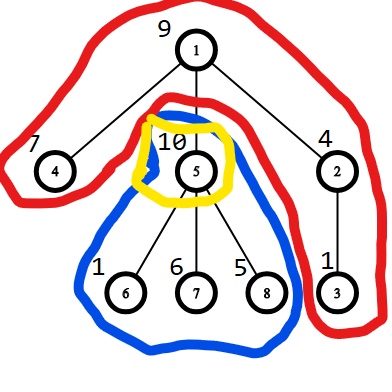
假设 fa = 1， u = 5（即从根为1 转换为根为 5）

由上图可以发现 红色部分的每一个结点都会与 根：u 多连了一条边 ，即红色部分的贡献要加倍（相当于深度+1，所有红色部分结点贡献）。

而红色部分就是 以 u 为根的子树之外的结点：即 ( Sum[ fa ] - Sum[ u ] );

蓝色部分的所有结点 都会与 根 u 少连一条边，即深度-1，蓝色部分结点贡献和减半;

以 fa = 1 为根时，总贡献和为 res；

转换为以 u = 5 为根时，总贡献和为 res + ( Sum[ fa ] - Sum[ u ]) - Sum[ u ];

当 u = 5 为根之后，

Sum[ fa ] = Sum[ fa ] - Sum[ u ] (即红色部分）因为树根变了，所以原本父亲的子树不再是整棵树，而是原来 以 u 为根的子树之外的结点。

Sum[ u ] = res; u 成为整棵树的根，整棵树都是 u 的子树。

按照这种方式递归搜索更新，取最大的res；

递归返回后，还原 Sum[ fa ], Sum[ u ], res 再搜索下一个儿子结点;

AC code：

 #include <cstdio>
 #include <iostream>
 #include <cstring>
 #define FOR(x, maxx) for(x = 1; x <= maxx; x++)
 #define ZERO(aa, x) memset(aa, x, sizeof(aa))
 #define INF 0x3f3f3f3f
 #define LL long long
 using namespace std;

 const int MAXN = 2e5+;

 struct EDGE
 {
     int v, nxt;
 }edge[MAXN<<];
 int head[MAXN];
 LL sum[MAXN], sumk[MAXN];

 int cost[MAXN], dep[MAXN];
 int N, cnt;
 LL ans, res;

 void add(int from, int to)
 {
     edge[cnt].v = to;
     edge[cnt].nxt = head[from];
     head[from] = cnt++;
 }
 void init()
 {
     memset(head, -, sizeof(head));
     cnt = ;
     ans = ;
 }

 void dfs1(int now, int dh, int fa)
 {
     //puts("zjy");ans = max(res, ans);
     int to;
     sum[now] = cost[now];
     res += 1LL*cost[now]*dh;
 //    dep[now] = dh;
 //    f[now] = fa;
     //printf("now: %d\n", now);
     for(int i = head[now]; i != -; i = edge[i].nxt){
         to = edge[i].v;
         if(to != fa){
             dfs1(to, dh+, now);
             sum[now]+=sum[to];
         }
     }
 }

 void dfs2(int now, int fa)
 {
     ans = max(res, ans);
     int to;
     LL a, b, c;
     for(int i = head[now]; i != -; i = edge[i].nxt){
         to = edge[i].v;
         if(to == fa) continue;
         a = sum[now], b = sum[to], c = res;
         res-=sum[to];               //当前子树的节点距离-1
         res+=sum[now]-sum[to];      //当前非子树节点距离+1
         sum[now]-=sum[to];
         sum[to] = a;
         dfs2(to, now);
         sum[now] = a;   //还原
         sum[to] = b;
         res = c;
     }
 }

 int main()
 {
     int i, j;
     init();
     scanf("%I64d", &N);
     FOR(i, N) scanf("%I64d", &cost[i]);
     int u, v;
     for(i = ; i < N; i++){
         scanf("%d %d", &u, &v);
         add(u, v);
         add(v, u);
     }
     //puts("zjy");
     dfs1(, , );      //第一次递归求初始值
     dfs2(, );
     printf("%I64d\n", ans);
     return ;
 }

二、树形dp

同样需要一次DFS 预处理出 s[ u ] 以 u 为根的子树的贡献总和（包括 u 结点本身);

状态：dp[ u ]  以 u 为根时，整棵树的贡献和

状态转移：dp[u] = dp[fa] + sum - 2*s[u]； （ sum 为所有结点的权值总和）

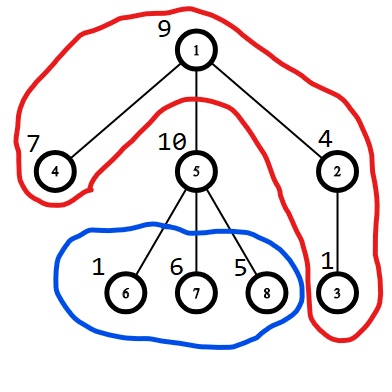
假设 fa = 1，u = 5；

dp[ 5 ] = dp[ 1 ] + 红色 - 蓝色 - cost[ u ];

dp[ 5 ] = dp[ 1 ] + ( sum - s[ 5 ]) - s[ 5 ];

dp[ 5 ] = dp[ 1 ]  + sum - 2*s[ 5 ];

AC code:

 #include <cstdio>
 #include <iostream>
 #include <cstring>
 #define FOR(x, maxx) for(x = 1; x <= maxx; x++)
 #define ZERO(aa, x) memset(aa, x, sizeof(aa))
 #define INF 0x3f3f3f3f
 #define LL long long
 using namespace std;

 const int MAXN = 2e5+;

 struct EDGE
 {
     int v, nxt;
 }edge[MAXN<<];
 int head[MAXN], cnt;;
 LL sum[MAXN], dp[MAXN];
 LL cost[MAXN];
 LL ans, res;
 LL SSum;
 int N;

 void add(int from, int to)
 {
     edge[cnt].v = to;
     edge[cnt].nxt = head[from];
     head[from] = cnt++;
 }
 void init()
 {
     memset(head, -, sizeof(head));
     memset(dp, , sizeof(dp));
     SSum = 0LL;
     cnt = ;
     ans = ;
 }

 void dfs(int now, int fa)
 {
     int to;
     sum[now] = cost[now];
     for(int i = head[now]; i != -; i = edge[i].nxt){
         to = edge[i].v;
         if(to == fa) continue;
         dfs(to, now);
         sum[now]+=sum[to];
         dp[now] = dp[now] + dp[to] + sum[to];
     }
 }

 void solve(int now, int fa)
 {
     int to;
     if(fa) dp[now] = dp[fa]+SSum-*sum[now];
     for(int i = head[now]; i != -; i = edge[i].nxt){
         to = edge[i].v;
         if(to == fa) continue;
         solve(to, now);
     }
     ans = max(ans, dp[now]);
 }

 int main()
 {
     init();
     scanf("%d", &N);
     for(int i = ; i <= N; i++){
         scanf("%I64d", &cost[i]);
         SSum+=cost[i];
     }
     int u, v;
     for(int i = ; i < N; i++){
         scanf("%d %d", &u, &v);
         add(u, v);
         add(v, u);
     }
     //puts("zjy");
     dfs(, );      //第一次递归求初始值
     solve(, );
     printf("%I64d\n", ans);
     return ;
 }