【BZOJ3144】[Hnoi2013]切糕 最小割

【BZOJ3144】[Hnoi2013]切糕

Description

Input

第一行是三个正整数P,Q,R，表示切糕的长P、 宽Q、高R。第二行有一个非负整数D，表示光滑性要求。接下来是R个P行Q列的矩阵，第z个 矩阵的第x行第y列是v(x,y,z) (1≤x≤P, 1≤y≤Q, 1≤z≤R)。 
100%的数据满足P,Q,R≤40，0≤D≤R，且给出的所有的不和谐值不超过1000。

Output

仅包含一个整数，表示在合法基础上最小的总不和谐值。

Sample Input

2 2 2
1
6 1
6 1
2 6
2 6

Sample Output

6

HINT

最佳切面的f为f(1,1)=f(2,1)=2,f(1,2)=f(2,2)=1

题解：APIO上学到了这种建图方法，赶紧%一发

先不考虑D的限制，那么原题就是无脑最小割，图大概长这样(只考虑两个纵轴)

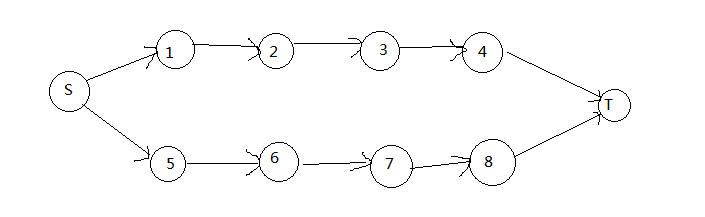
但如果加上这条限制，我们该怎么做？这里先给出结论，假设D=1，从7->2连一条∞的边，从3->6连一条∞的边（其余同理），原图变成了这样

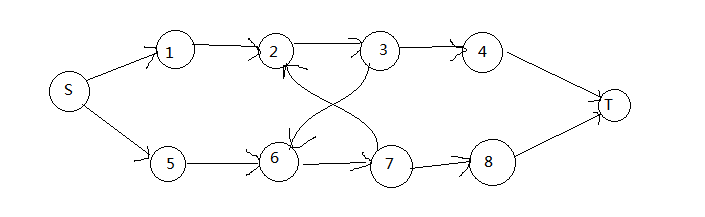
（画图软件有点尴尬~）

发现如果这样连边，我们就可以防止(1,2)与(7,8)同时被割掉，因为就算割掉这两条边，S仍然可以通过5-6-3-4与T联通，所以只能割别的边

一开始我比较懒，省略了S->1,4->T这两条长度为∞的边，结果狂WA不止，后来发现R可以等于1。。。

#include <cstdio>
#include <iostream>
#include <cstring>
#include <queue>
#define P(A,B,C) ((C-1)*n*m+(B-1)*n+A)
using namespace std;
const int maxm=1000000;
const int maxn=100010;
queue<int> q;
int n,m,h,S,T,D,cnt,ans;
int to[maxm],next[maxm],val[maxm],head[maxn],d[maxn];
int dx[]={1,0,-1,0},dy[]={0,1,0,-1};
int rd()
{
	int ret=0,f=1;	char gc=getchar();
	while(gc<'0'||gc>'9')	{if(gc=='-')f=-f;	gc=getchar();}
	while(gc>='0'&&gc<='9')	ret=ret*10+gc-'0',gc=getchar();
	return ret*f;
}
int bfs()
{
	memset(d,0,sizeof(d));
	while(!q.empty())	q.pop();
	int i,u;
	d[S]=1,q.push(S);
	while(!q.empty())
	{
		u=q.front(),q.pop();
		for(i=head[u];i!=-1;i=next[i])
		{
			if(!d[to[i]]&&val[i])
			{
				d[to[i]]=d[u]+1;
				if(to[i]==T)	return 1;
				q.push(to[i]);
			}
		}
	}
	return 0;
}
int dfs(int x,int mf)
{
	if(x==T)	return mf;
	int i,k,temp=mf;
	for(i=head[x];i!=-1;i=next[i])
	{
		if(d[to[i]]==d[x]+1&&val[i])
		{
			k=dfs(to[i],min(temp,val[i]));
			if(!k)	d[to[i]]=0;
			val[i]-=k,val[i^1]+=k,temp-=k;
			if(!temp)	break;
		}
	}
	return mf-temp;
}
void add(int a,int b,int c)
{
	to[cnt]=b,val[cnt]=c,next[cnt]=head[a],head[a]=cnt++;
	to[cnt]=a,val[cnt]=0,next[cnt]=head[b],head[b]=cnt++;
}
int main()
{
	n=rd(),m=rd(),h=rd(),D=rd();
	memset(head,-1,sizeof(head));
	int i,j,k,l;
	S=0,T=n*m*h+1;
	for(k=1;k<=h;k++)
	{
		for(i=1;i<=n;i++)
		{
			for(j=1;j<=m;j++)
			{
				if(k==1)	add(S,P(i,j,k),rd());
				else	add(P(i,j,k-1),P(i,j,k),rd());
				if(k==h)	add(P(i,j,k),T,1<<30);
				if(k>D)	for(l=0;l<4;l++)	if(i+dx[l]&&i+dx[l]<=n&&j+dy[l]&&j+dy[l]<=m)
					add(P(i,j,k),P(i+dx[l],j+dy[l],k-D),1<<30);
			}
		}
	}
	while(bfs())	ans+=dfs(S,1<<30);
	printf("%d",ans);
	return 0;
}