【hdu1255】线段树求矩形面积交

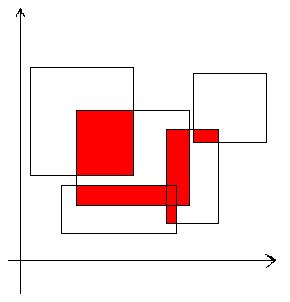
题意大概就是上图这个样子。<=100组测试数据，每组<=1000个矩形。

题解：

这个问题怎么解决。。做了上一题矩形面积并应该就会了。。

对于每个节点维护3个值：

cnt：该节点所代表的这条线段被覆盖了多少次

len1：该节点所管理区间中被覆盖了>=1次的线段总长

len2：该节点所管理区间中被覆盖了>=2次的线段总长

为什么要维护两个呢？因为要是只维护len2，那子树中要是有个覆盖了一次的，然后该节点覆盖一次，那么怎么更新len2丫。。

怎么更新？

 void upd(int x)
 {
     int lc=t[x].lc,rc=t[x].rc;
     if(t[x].cnt>=) //如果该点被覆盖了两次
         t[x].len1=t[x].len2=t[x].rl;//len1和len2=该节点所代表线段的长度
     if(t[x].cnt==)//如果该点只被覆盖了一次
     {
         t[x].len1=t[x].rl;//len1=全长
         t[x].len2=t[lc].len1+t[rc].len1;//孩子中有些只被覆盖了一次的变成覆盖了两次
     }
     if(t[x].cnt==)//如果没被覆盖，那就直接上传更新。
     {
         t[x].len1=t[lc].len1+t[rc].len1;
         t[x].len2=t[lc].len2+t[rc].len2;
     }
 }

一开始我在纠结一种情况：一个节点现在被覆盖一次，它的子树中原本有个节点被覆盖了一次，那么怎么更新？维护一个从根节点往下的sum值吗？

后来我发现该节点的len2可以直接用孩子的len1更新就好。

弱弱弱弱弱弱弱弱弱弱弱弱弱弱弱弱

 #include<cstdio>
 #include<cstdlib>
 #include<cstring>
 #include<cmath>
 #include<iostream>
 #include<algorithm>
 using namespace std;

 const int N=,INF=(int)1e9;
 double z[N][];
 struct point{
     double d;
     int x,y;
 }p[*N];
 struct node{
     int x0,x1,d;
     double y;
 }a[N];
 struct trnode{
     int l,r,lc,rc,cnt,lazy;
     double rl,len1,len2;
     //len1以x为根的子树中表示被覆盖了>=1次的线段长度，len2表示以x为根的子树中被覆盖了>=2次的线段的长度
 }t[*N];
 double num[N];
 int n,tl,pl,al;

 int minn(int x,int y){return x<y ? x:y;}
 int maxx(int x,int y){return x>y ? x:y;}
 bool cmp_d(point x,point y){return x.d<y.d;}
 bool cmp_y(node x,node y){return x.y<y.y;}

 int bt(int l,int r)
 {
     int x=++tl;
     t[x].l=l;t[x].r=r;
     t[x].lc=t[x].rc=;
     t[x].cnt=;t[x].lazy=;
     t[x].len1=t[x].len2=;
     t[x].rl=num[r+]-num[l];
     if(l<r)
     {
         int mid=(l+r)/;
         t[x].lc=bt(l,mid);
         t[x].rc=bt(mid+,r);
     }
     return x;
 }

 void upd(int x)
 {
     int lc=t[x].lc,rc=t[x].rc;
     if(t[x].cnt>=) //如果该点被覆盖了两次
         t[x].len1=t[x].len2=t[x].rl;//len1和len2=该节点所代表线段的长度
     if(t[x].cnt==)//如果该点只被覆盖了一次
     {
         t[x].len1=t[x].rl;//len1=全长
         t[x].len2=t[lc].len1+t[rc].len1;//孩子中有些只被覆盖了一次的变成覆盖了两次
     }
     if(t[x].cnt==)//如果没被覆盖，那就直接上传更新。
     {
         t[x].len1=t[lc].len1+t[rc].len1;
         t[x].len2=t[lc].len2+t[rc].len2;
     }
 }

 void change(int x,int l,int r,int d,int sum)
 {
     if(t[x].l==l && t[x].r==r)
     {
         t[x].cnt+=d;
         upd(x);
         return ;
     }
     int lc=t[x].lc,rc=t[x].rc,mid=(t[x].l+t[x].r)/;
     if(r<=mid) change(lc,l,r,d,sum+t[x].cnt);
     else if(l>mid) change(rc,l,r,d,sum+t[x].cnt);
     else
     {
         change(lc,l,mid,d,sum+t[x].cnt);
         change(rc,mid+,r,d,sum+t[x].cnt);
     }
     upd(x);
 }

 void output()
 {
     for(int i=;i<=tl;i++)
         printf("l = %d  r = %d  cnt = %d  len1  = %lf  len2 = %lf  rl = %lf \n",t[i].l,t[i].r,t[i].cnt,t[i].len1,t[i].len2,t[i].rl);
 }

 int main()
 {
     freopen("a.in","r",stdin);
     int T;
     scanf("%d",&T);
     while(T--)
     {
         scanf("%d",&n);
         if(n==) break;
         int x,mx;pl=;tl=;al=;t[].len1=t[].len2=;
         for(int i=;i<=n;i++)
         {
             for(int j=;j<=;j++)
             {
                 scanf("%lf",&z[i][j]);
                 if(j%==) p[++pl].d=z[i][j],p[pl].x=i,p[pl].y=j;
             }
         }
         sort(p+,p++pl,cmp_d);
         mx=;p[].d=INF;
         for(int i=;i<=pl;i++)
         {
             if(p[i].d!=p[i-].d) mx++,num[mx]=p[i].d;
             z[p[i].x][p[i].y]=mx;
         }
         bt(,mx-);//debug n个节点只有n-1条线段
         for(int i=;i<=n;i++)
         {
             if(z[i][]<z[i][]) swap(z[i][],z[i][]);
             if(z[i][]>z[i][]) swap(z[i][],z[i][]);
             a[++al].x0=z[i][];a[al].x1=z[i][];a[al].y=z[i][];a[al].d=-;
             a[++al].x0=z[i][];a[al].x1=z[i][];a[al].y=z[i][];a[al].d=;
         }
         sort(a+,a++al,cmp_y);
         double w,h,ans=;
         change(,a[].x0,a[].x1-,a[].d,);
         for(int i=;i<=al;i++)
         {
             h=a[i].y-a[i-].y;
             w=t[].len2;
             ans+=w*h;
             change(,a[i].x0,a[i].x1-,a[i].d,);
         }
         printf("%.2lf\n",ans);
     }
     return ;
 }