P vs NP

• Complexity Class
• Computational problem
  • Decision Problems
  • Model of computation
  • Time-complexity classes
  • Space-complexity classes
• P, NP, co-NP, NPC, NP-hard
  • P
  • NP
  • co-NP
  • NPC
  • NP-hard
  • Euler图
• Reference

用计算机解决问题时，我们总希望算法足够快，因为任何时候资源都是相对不足的，特别是时间资源。
P vs NP是信息科学的最高峰。

Complexity Class

计算复杂度理论中，一个复杂类（Complexity Class）是与基于资源的复杂性相关的一个问题集，也就是在某种资源的视角下对问题的类别划分。
In computational complexity theory, a complexity class is a set of problems of related resource-based complexity. A typical complexity class has a definition of the form:
the set of problems that can be solved by an abstract machine M using O(f(n)) of resource R, where n is the size of the input.

Computational problem

The most commonly used problems are decision problems. However, complexity classes can be defined based on function problems (an example is FP), counting problems (e.g. #P), optimization problems, promise problems, etc.

Decision Problems

选择问题（判定问题）是答案为yes或no的问题。
A decision problem is a problem that can be posed as a yes-no question of the input values.

Model of computation

DTM：确定性图灵机，每个符号和状态的组合在action table中只对应一个输出。也就是没有随机性。
The most common model of computation is the deterministic Turing machine, but many complexity classes are based on nondeterministic Turing machines(NDTM), boolean circuits, quantum Turing machines, monotone circuits, etc.

Time-complexity classes

Model of computation	Time constraint f(n)	Time constraint poly(n)	Time constraint 2^poly(n)
DTM	DTIME	p	EXPTIME
NDTM	NTIME	NP	NEXPTIME

Space-complexity classes

Model of computation	Space constraint f(n)	Space constraint O(log n)	Space constraint poly(n)	Space constraint 2^poly(n)
DTM	DSPACE	L	PSPACE	EXPSPACE
NDTM	NSPACE	NL	NPSPACE	NEXPSPACE

P, NP, co-NP, NPC, NP-hard

这些都是时间复杂度下的complexity class。

P

P包含所有使用DTM，在多项式时间（Polynomial Time）内可解的decision问题。
It contains all decision problems that can be solved by a deterministic Turing machine using a polynomial amount of computation time, or polynomial time.

P包含很多自然问题，包含decision版本的线性规划，求最大公约数，寻找最大配对。
P is known to contain many natural problems, including the decision versions of linear programming, calculating the greatest common divisor, and finding a maximum matching.

NP

NP是使用NDTM在多项式时间可解的decision问题集。
Equivalently, the formal definition of NP is the set of decision problems solvable in polynomial time by a theoretical non-deterministic Turing machine.

NP更直观的理解：该类问题可以先去猜测一个解，这个过程是非确定的（non-deterministic way），但可以用确定性算法去验证或拒绝（reject）这个解。
NP问题没有已知的快速解法（不是没有解法，也不确定就是没有快速解法，快速是指多项式级别），通常采用启发式（Heuristic）算法、近似、随机、参数化方法，或将问题限制在一定的条件下。
很多搜索和优化问题属于NP问题，所以有时候用启发式搜索，机器学习中用SGD训练算法。

co-NP

当且仅当一个decision问题的补(complement)属于NP时，该问题属于co-NP。也就是说，该类问题的否定回答可以在多项式时间内由NDTM验证为正确。
A decision problem is a member of co-NP if and only if its complement is in the complexity class NP. Equivalently, co-NP is the set of decision problems where the "no" instances can be accepted in polynomial time by a non-deterministic Turing machine.

举例：给定一个有限整数集，是否每个非空子集都有非零和。
An example of an NP-complete problem is the subset sum problem: given a finite set of integers, is there a non-empty subset that sums to zero? To give a proof of a "yes" instance, one must specify a non-empty subset that does sum to zero. The complementary problem is in co-NP and asks: "given a finite set of integers, does every non-empty subset have a non-zero sum?".

NPC

P包含在NP中，但是NP中有很多重要的问题，其中最困难的是NP-complete问题，其解决方法可以在多项式时间内应用到其他任何NP问题。
The complexity class P is contained in NP, but NP contains many important problems, the hardest of which are called NP-complete problems, whose solutions are sufficient to deal with any other NP problem in polynomial time.

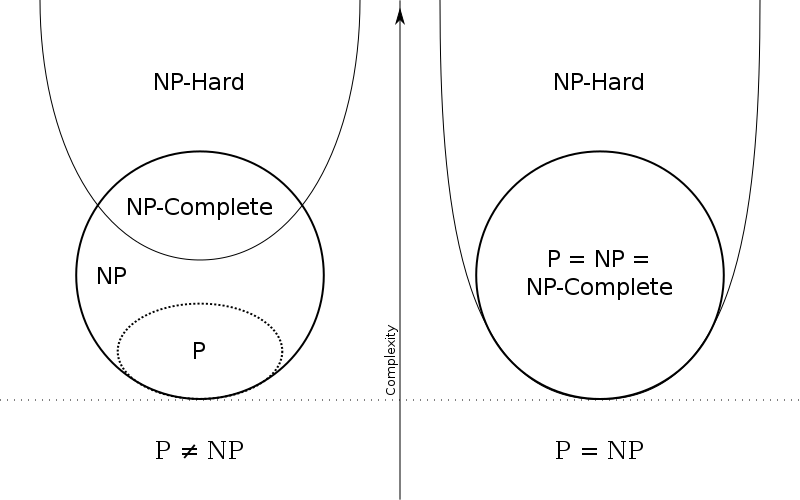
"是否P=NP"是复杂性理论中最重要的开放性（未被证明）问题，它问的是NPC问题是否存在多项式时间的解法，而按照推论，等价于所有NP是否存在多项式时间的解法。普遍认为这是不可能的。（通用解法，这种东西，不存在的/smilence）
The most important open question in complexity theory, the P versus NP ("P=NP") problem, asks whether polynomial time algorithms actually exist for solving NP-complete, and by corollary, all NP problems. It is widely believed that this is not the case.

The complexity class NP (which have efficiently verifiable proofs where the answer is "yes") is also related to the complexity class co-NP (which have efficiently verifiable proofs where the answer is "no"). Whether or not NP = co-NP is another outstanding question in complexity theory.

NP-hard

NP-hard至少和NP问题一样困难，所有的NP问题都可以规约到（reduce to）它们，但NP-hard问题不一定可以在多项式时间内验证，也就是说不一定是NP的。
NP-hard problems are those at least as hard as NP problems, i.e., all NP problems can be reduced (in polynomial time) to them. NP-hard problems need not be in NP, i.e., they need not have solutions verifiable in polynomial time.

训练深度神经网络和很多机器学习系统都是NP-hard问题。（Sanjeev Arora, Aditya Bhaskara, Rong Ge, and Tengyu Ma. Provable bounds for learning some deep representations. CoRR, abs/1310.6343, 2013.）

Euler图

Reference

Decision problem
Complexity classes
P
NP
P vs NP
Heuristic
A sina blog about NP by xuelinger_2010