红黑树插入操作---以JDK 源码为例

红黑树遵循的条件：

1.根节点为黑色。

2.外部节点（叶子节点）为黑色。

3.红色节点的孩子节点为黑色。（由此，红色节点的父节点也必为黑色）

4.从根节点到任一外部节点的路径上，黑节点的数量相同。

节点插入过程

 在红黑树中插入节点，首先调用查找接口，并在查找终止位置创建节点，并将节点染成红色。

 当新插入节点的父节点为红色时，不满足红黑树的条件，产生‘双红’现象。此时，需要对树的拓扑结构和节点颜色进行调节。

双黑修正过程

 以JDK TreeMap.class 中定义的红黑树类中插入修正函数为例，函数定义如下：

 在这里约定插入节点为x，插入节点的父节点为p，祖父节点为g，曾祖父节点为gg，叔叔节点为u。双红修正根据插入节点周围的相关节点的不同情况，进行相应调整，分为以下几种情况：

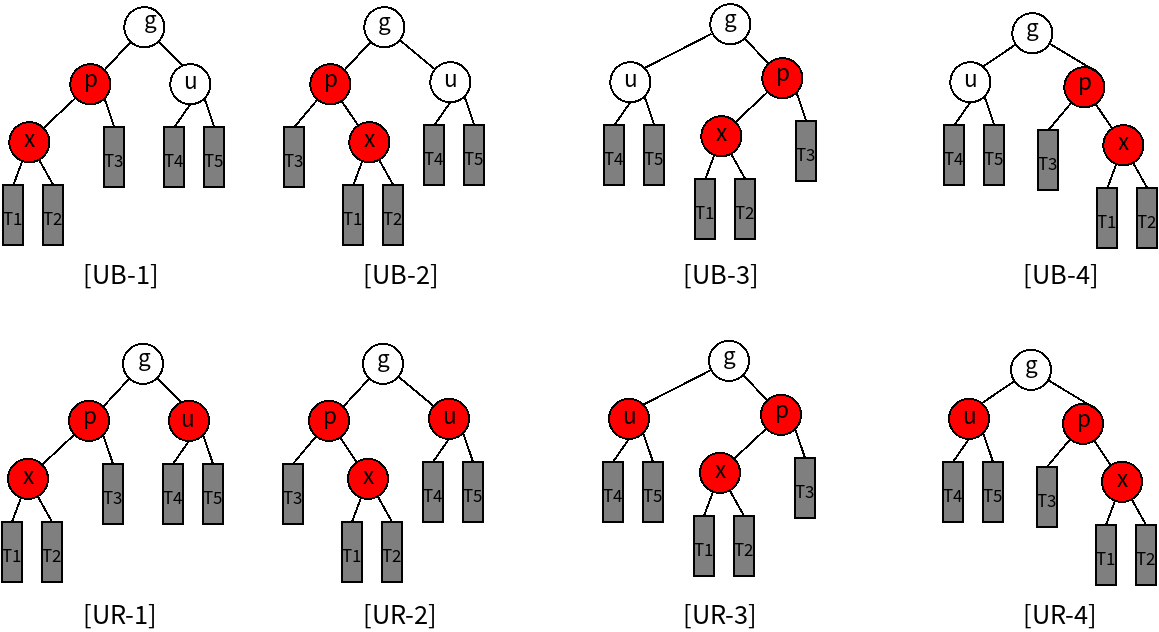
修正方法：

1.对于叔叔节点为黑色的情况[UB 1-4]

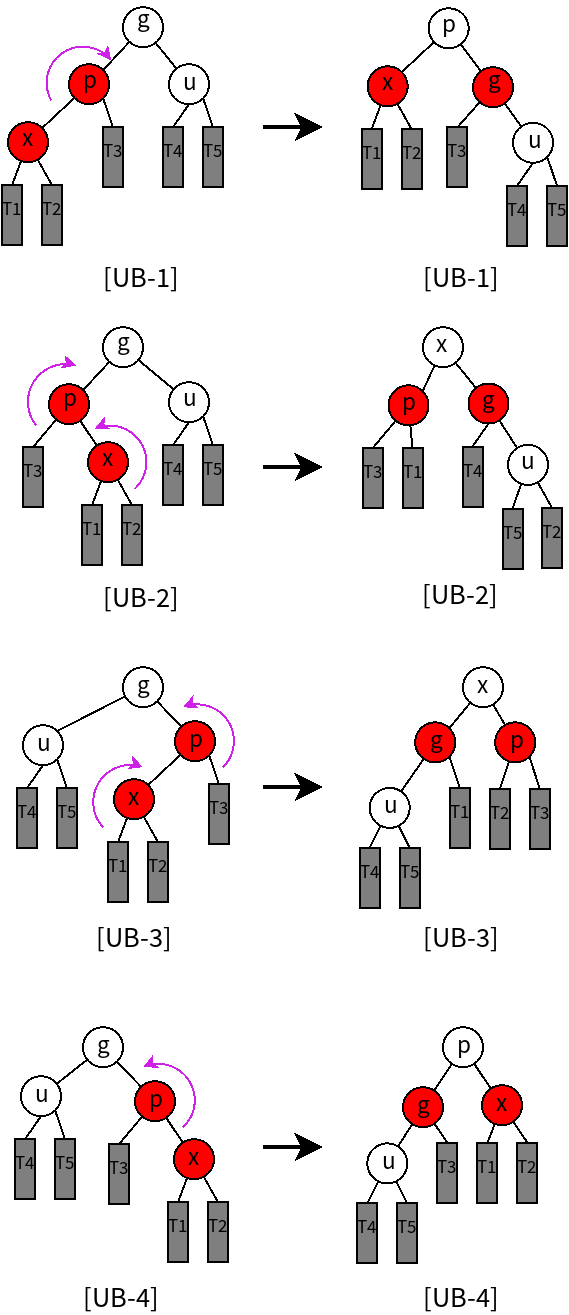
需要进行1至2次旋转（相当于进行3-4重构）。并对节点进行重新染色，使之满足红黑树约束条件,如下图所示。修正后该局部的最高节点为黑色，所以双红现象不会向上传播，因此，经过本步骤修正后即可使红黑树合法。

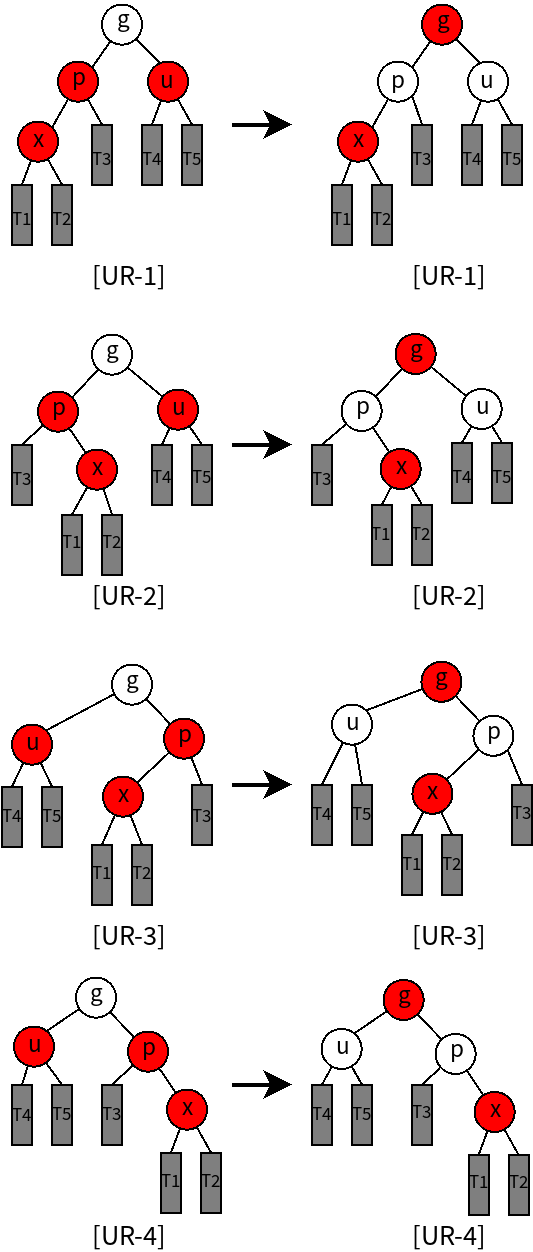
2.对于叔叔节点为红色的情况[UR 1-4]

无需要旋转，而仅需对插入节点及相关节点进行重新染色，使之满足红黑树约束条件,如下图所示。修正后该局部的最高节点变为红色，若曾祖父节点gg为红，则会产生新的双红现象，并可能依次向上传播，因此，需递归调用修正函数，继续向上修正，直到整个树合法。

源码剖析

源代码路径/usr/lib/jvm/java-8-openjdk-amd64/jre/lib/rt.jar!/java/util/TreeMap.class （笔者使用的linux上的路径，具体路径根据安装位置会有所不同）；

    private void fixAfterInsertion(TreeMap.Entry<K, V> var1) {
        var1.color = false;        //节点颜色，true：黑色        false：红色

        while(var1 != null && var1 != this.root && !var1.parent.color) {
            //节点非空，非根节点，且父节点为红色 ==>>需要继续向上进行双红修正

            TreeMap.Entry var2;
            if (parentOf(var1) == leftOf(parentOf(parentOf(var1)))) {
              //若插入节点的父节点p为祖父节点g的左孩子[UB-1,2][UR-1,2]

                var2 = rightOf(parentOf(parentOf(var1)));                 //插入节点的叔叔节点U
                if (!colorOf(var2)) {                                     //叔叔节点为红色[UR-1,2]
                    setColor(parentOf(var1), true);                       //----重新染色----//
                    setColor(var2, true);                                 //----重新染色----//
                    setColor(parentOf(parentOf(var1)), false);            //----重新染色----//
                    var1 = parentOf(parentOf(var1));                      //节点上升，准备向上修正
                } else {                                                  //叔叔节点为黑色[UB-1,2]
                    if (var1 == rightOf(parentOf(var1))) {                //插入节点x为右孩子 [UB-2]
                        var1 = parentOf(var1);
                        this.rotateLeft(var1);                            //先左旋
                    }
                                                                          //插入节点x为右孩子 [UB-1]
                    setColor(parentOf(var1), true);                       //----重新染色----//
                    setColor(parentOf(parentOf(var1)), false);            //----重新染色----//
                    this.rotateRight(parentOf(parentOf(var1)));           //后右旋
                }
            } else {
                //若插入节点的父节点p为祖父节点g的右孩子[UB-3,4][UR-3,4]

                var2 = leftOf(parentOf(parentOf(var1)));                  //取得叔叔节点
                if (!colorOf(var2)) {                                     //叔叔节点为红色[UR-3,4]
                    setColor(parentOf(var1), true);                       //----重新染色----//
                    setColor(var2, true);                                 //----重新染色----//
                    setColor(parentOf(parentOf(var1)), false);            //----重新染色----//
                    var1 = parentOf(parentOf(var1));                      //节点上升，准备向上修正
                } else {                                                  //叔叔节点为黑色[UB-3,4]
                    if (var1 == leftOf(parentOf(var1))) {                 //插入节点x为左孩子[UB-3]
                        var1 = parentOf(var1);                            //
                        this.rotateRight(var1);                           //先右旋
                    }
                                                                          //插入节点x为右孩子[UB-4]
                    setColor(parentOf(var1), true);                       //----重新染色----//
                    setColor(parentOf(parentOf(var1)), false);            //----重新染色----//
                    this.rotateLeft(parentOf(parentOf(var1)));            //左旋
                }
            }
        }

        this.root.color = true;                                           //为避免将根节点染红，总是进行修正
    }

 当插入节点的叔叔节点为红色时[UR],需要将祖父节点g染红，从而可能导致双红现象向上传播（当gg为红时）。此时，需要递归调用双红修正函数，继续向上修正，直至消除树中双红现象。

 在以上JDK代码中，并为出现函数递归调用，而是将递归调用更改为等价的迭代（while循环内）。在处理完叔叔节点为红的情况时，先进行染色，然后将当前节点x更新为其祖父节点g。在while循环内，持续进行修正。每循环一次，当将节点都会上升两层，直到到达根节点，或者gg为黑，修正即完成。

 当x节点的祖父节点g为根节点时，而叔叔节点为红色时，修正函数会将根节点g染红，而违反红黑树规则1，此时，只需将根节点g染黑即可使红黑树恢复合法（函数最后一行），这也是唯一增加树的黑高度的情况。

笔者在阅读代码时，还产生一些疑惑：在[UB-2,3]两种情况的处理过程中，会更新当前节点x，如下所示。

[UB-2]

                    if (var1 == rightOf(parentOf(var1))) {     //插入节点x为右孩子 [UB-2]
                        var1 = parentOf(var1);
                        this.rotateLeft(var1);                 //先左旋
                    }

[UB-3]

                    if (var1 == leftOf(parentOf(var1))) {      //插入节点x为左孩子[UB-3]
                        var1 = parentOf(var1);                 //
                        this.rotateRight(var1);                //先右旋
                    }

可以看到在旋转前，当前节点x会被替换为其父节点p，然后在对其进行旋转。来看一下旋转函数的定义：

    private void rotateLeft(TreeMap.Entry<K, V> var1) {
        if (var1 != null) {
            TreeMap.Entry var2 = var1.right;    //[1]
            var1.right = var2.left;             //[2]
            if (var2.left != null) {
                var2.left.parent = var1;        //[3]
            }

            var2.parent = var1.parent;          //[4]
            if (var1.parent == null) {
                this.root = var2;               //[5]
            } else if (var1.parent.left == var1) {
                var1.parent.left = var2;        //[6]
            } else {
                var1.parent.right = var2;       //[6']
            }

            var2.left = var1;                    //[7]
            var1.parent = var2;                  //[8]
        }

    }

函数中各步骤用图表达为：



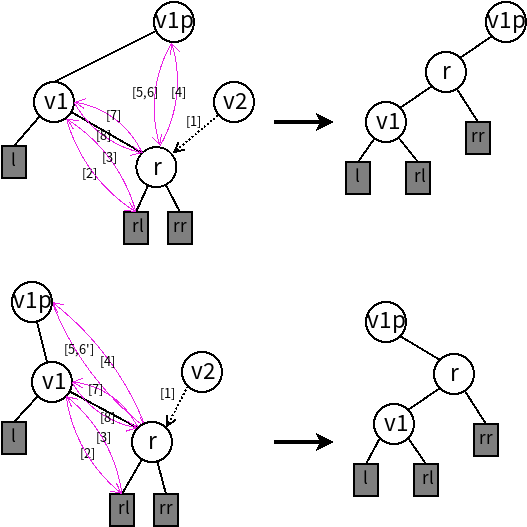
 设x为当前节点x_old，其在fixAfterInsertion中被上升到父节点x=p，对x调用rotateLeft后，x的高度将降低一层，与原来的旧值x_old处于同一层次。这样在后续进行右旋或左旋时，即可对不同层次进行正确的染色。

 以上图为例，若节点v1p为根节点，则节点r的原深度为3，在fixAfterInsertion中被上升到父节点r=p后，r的深度为2，在对r调用rotateLeft后，r的深度恢复为3，此后再对r调用parentOf后，即可得到深度为2的父节点，对r调用parentOf-parentOf后，得到深度为1的祖父节点，从而确保不同层次的节点被正确染色。右旋的情况左旋相类似。

 由此可以得出结论：在对节点x进行旋转前，先将其指向父节点p，然后实施旋转，此后进行的染色即可和只需要一次旋转的操作保持一致性，使代码更加紧凑。