P1058 立体图题解

小渊是个聪明的孩子，他经常会给周围的小朋友们将写自己认为有趣的内容。最近，他准备给小朋友们讲解立体图，请你帮他画出立体图。

小渊有一块面积为m \times nm×n的矩形区域，上面有m \times nm×n个边长为11的格子，每个格子上堆了一些同样大小的积木（积木的长宽高都是11），小渊想请你打印出这些格子的立体图。我们定义每个积木为如下格式，并且不会做任何翻转旋转，只会严格以这一种形式摆放：

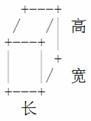
每个顶点用11个加号’++’表示，长用33个”-−”表示，宽用11个”/”，高用两个”|”表示。字符’++’,”-−”,”/”,”|”的ASCIIASCII码分别为4343，4545，4747，124124。字符’.’(ASCIIASCII码4646)需要作为背景输出，即立体图里的空白部分需要用’.’来代替。立体图的画法如下面的规则：

若两块积木左右相邻，图示为：

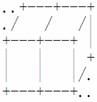
若两块积木上下相邻，图示为：

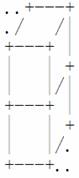
若两块积木前后相邻，图示为：

立体图中，定义位于第(m,1(m,1)的格子（即第mm行第11列的格子）上面自底向上的第一块积木（即最下面的一块积木）的左下角顶点为整张图最左下角的点。

输入输出格式

输入格式：

第一行有用空格隔开的22个整数mm和nn，表示有m \times nm×n个格子(1 \le m,n \le 50)(1≤m,n≤50)。

接下来的mm行，是一个m \times nm×n的矩阵，每行有nn个用空格隔开的整数，其中第ii行第jj列上的整数表示第ii行第jj列的个子上摞有多少个积木（1 \le1≤每个格子上的积木数\le 100≤100）。

输出格式：

输出包含题目要求的立体图，是一个KK行LL列的字符串矩阵，其中KK和LL表示最少需要KK行LL列才能按规定输出立体图。

---

题解部分：

题都读不懂？

其实就是给你长宽，给你三视图（主，侧，俯）中的俯视图，然后让你画它的三维立体图。

本题思路源泉：P1003 铺地毯

也就是一个覆盖的思想。

众所周知，三维图要满足遮挡关系，也就是前面的遮挡后面的，右面的遮挡左边的。

那么我们用透视关系来覆盖。

那么我们枚举每一个二维方块位置，然后在每一个二维平面位置上一个一个网上摞方块就可以了。

具体的，因为每一个方块为一个面积，那么我们只能抽象成一个点来进行枚举

我们把一个方块抽象为左上角的点，于是枚举左上角的点再进行覆盖。

这个题就这样了。。

代码：

#include<cstdio>
#include<iostream>
using namespace std;
int read(){
    int ans=;
    char last=' ',ch=getchar();
    while(ch<''||ch>'')
    last=ch,ch=getchar();
    while(ch>=''&&ch<='')
    {
        ans=(ans<<)+(ans<<)+(ch^);
        ch=getchar();
    }
    return last=='-'?-ans:ans;
}
char c[][],c1[][]={//倒着存储
    "+---+",
    "|   |/",
    "|   | +",
    "+---+ |",
    " /   /|",
    "  +---+",
    };//6行7列 的方块
int n,m,jz[][],maxh=-,maxl=-,zbx,zby;
inline void fg(int zbx,int zby)//覆盖操作
{
    for(int i=;i<=;i++)c[zbx][zby+i]=c1[][i];
    for(int i=;i<=;i++)c[zbx+][zby+i]=c1[][i];
    for(int i=;i<=;i++)c[zbx+][zby+i]=c1[][i];
    for(int i=;i<=;i++)c[zbx+][zby+i]=c1[][i];
    for(int i=;i<=;i++)c[zbx+][zby+i]=c1[][i];
    for(int i=;i<=;i++)c[zbx+][zby+i]=c1[][i];
}
int main(){
//    freopen("drawing.in","r",stdin);
//    freopen("drawing.out","w",stdout);
    m=read();n=read();
    for(int i=;i<=m;i++)
    {
        for(int j=;j<=n;j++)
        {
            jz[i][j]=read();
        }
    }
    for(int i=;i<=m;i++)//从输入的矩阵的左上角开始，满足先后，先左
        for(int j=;j<=n;j++)
        {
            zbx=(m-i)*+;zby=(m-i)*++*(j-);
            for(int k=;k<=jz[i][j];k++,zbx+=)
            {
                fg(zbx,zby);
            }
            if(zbx+>maxh)maxh=zbx+;//我不知道为什么
            if(zby+>maxl)maxl=zby+;
        }
    for(int i=maxh;i>=;i--)
    {
        for(int j=;j<=maxl;j++)
        {
            if(c[i][j]=='\0') printf(".");
            else
            printf("%c",c[i][j]);
        }
        printf("\n");
    }
    return ;
}

完结