Leetcode Lect7 哈希表

传统的哈希表

对于长度为n的哈希表，它的存储过程如下:

    根据 key 计算出它的哈希值 h=hash(key)

    假设箱子的个数为 n，那么这个键值对应该放在第 (h % n) 个箱子中

    如果该箱子中已经有了键值对，就使用开放寻址法或者拉链法解决冲突

哈希冲突

如果不同字符串被hash到了同一个位置，称为哈希冲突。解决哈希冲突的常用办法有以下几种：

拉链法（开哈希）

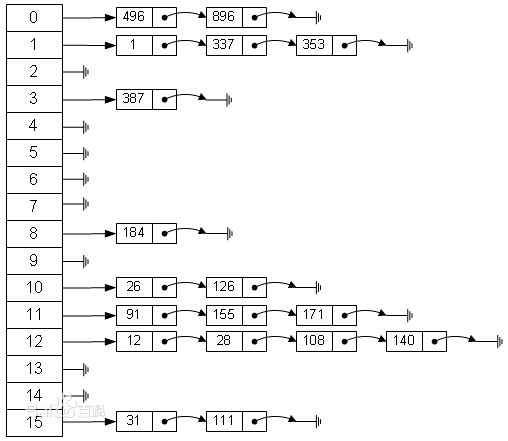
在使用拉链法解决哈希冲突时，对于每一个数组位置，放置的元素相当于一个链表，属于同一个箱子的所有键值对都会排列在链表中。当有冲突时，我们将这个元素插入到链表尾部，以此来避免冲突。

线性探测法（闭哈希）

线性探测法属于开放定址法的一种。

当冲突发生的时候，我们检查冲突的哈希地址的下一位（数组下标加一），判断能否插入，如果不能则再继续检查下一个位置。

在拉链法实现的哈希表中，因为链表的存在，可以弹性地容纳键值对，而对于线性探测法实现的哈希表，其容纳键值对的数量是直接受到数组大小的限制的。所以必须在数组充满以前调整数组的大小。一般来说，每当总键值对的对数达到数组的一半后，我们就将整个数组的大小扩大一倍。

闭哈希用的不多，因为一直往下一位插入会导致越来越多的collision

重哈希

这种方法是同时构造多个不同的哈希函数：

Hi=RH1(key) i=1，2，…，k

当哈希地址Hi=RH1（key）发生冲突时，再计算Hi=RH2（key）……，直到冲突不再产生。这种方法不易产生聚集，但增加了计算时间。

哈希表的扩容

一般来说，每当总键值对的对数达到数组的一半后，我们就将整个数组的大小扩大一倍。扩容时要把所有的元素重新计算hash并插入到更大容量的新哈希表中。

分布式哈希表

参考DHT，将一张哈希表按hash值分割到不同机器上。

一致性哈希

在普通分布式哈希表中，如果有节点动态加入或者删除，就会导致大量数据失效。那么如何改进这一情况呢？

consistent hashing 是一种 hash 算法，简单的说，在移除 / 添加一个 cache 时，它能够尽可能小的改变已存在 key 映射关系。它的思想是把机器和数据都hash到同一个空间中。

比如在Chord算法里，每台节点负责它顺时针方向到下一个节点之前的这一区域的hash数据点。如果在这一区间内有节点的动态加入/删除，那么只有这一区间端点的两台机器会受影响，而其他机器都不会。

另外还有一种DHT算法叫做Kademlia，它就是P2P下载的基础。可以参考https://colobu.com/2018/03/26/distributed-hash-table/

红黑树

红黑树（Red-black Tree）是一种平衡排序二叉树（Balanced Binary Search Tree），在它上面进行增删查改的平均时间复杂度都是 O(logn)，是居家旅行的常备数据结构。

Q: 在面试中考不考呢？
A: 很少考……

Q: 需不需要了解呢？
A: 需要！

Q: 了解到什么程度呢？
A: 知道它是 Balanced Binary Search Tree，知道它支持什么样的操作，会用就行。不需要知道具体的实现原理。

红黑树的几个常用操作

Java当中，红黑树主要是TreeSet，位于java.util.TreeSet，继承自java.util.AbstractSet，它的主要方法有：

add，插入一个元素。
remove，删除一个元素。
clear，删除所有元素。
contains，查找是否包含某元素。
isEmpty，是否空树。
size，返回元素个数。
iterator，返回迭代器。
clone，对整棵树进行浅拷贝，即不拷贝元素本身。
first，返回最前元素。
last，返回最末元素。
floor，返回不大于给定元素的最大元素。
ceiling，返回不小于给定元素的最小元素。
pollFirst，删除并返回首元素。
pollLast，删除并返回末元素。

更具体的细节，请参考Java Reference。

此外，在Java当中，有一种map，用红黑树实现key查找，这种结构叫做TreeMap。如果你需要一种map，并且它的key是有序的，那么强烈推荐TreeMap。

在C++当中，红黑树即是默认的set和map，其元素也是有序的。
而通过哈系表实现的则分别是unordered_set和unordered_map，注意这两种结构是在C++11才有的。
在Python当中，默认的set和dict是用哈系表实现，没有默认的红黑树。如果你想使用红黑树的话，可以使用rbtree这个模块，下载地址：https://pypi.python.org/pypi/rbtree/0.9.0

Ref：https://xiekeyi98.com/819591f7.html