【HDOJ6608】Fansblog（威尔逊定理）

题意：给定质数p，求q!模p的值，其中q为小于p的最大质数

1e9<=p<=1e14

思路：根据质数密度近似分布可以暴力找q并检查

找到q后根据威尔逊定理：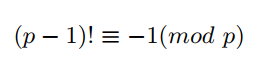

把q+1到p-1这一段的逆元移过去

 #include<bits/stdc++.h>
 using namespace std;
 typedef long long ll;
 typedef unsigned int uint;
 typedef unsigned long long ull;
 typedef pair<int,int> PII;
 typedef pair<ll,ll> Pll;
 typedef vector<int> VI;
 #define N  110000
 #define M  1100000
 #define fi first
 #define se second
 #define MP make_pair
 #define pi acos(-1)
 #define mem(a,b) memset(a,b,sizeof(a))
 #define rep(i,a,b) for(int i=(int)a;i<=(int)b;i++)
 #define per(i,a,b) for(int i=(int)a;i>=(int)b;i--)
 #define lowbit(x) x&(-x)
 #define Rand (rand()*(1<<16)+rand())
 #define id(x) ((x)<=B?(x):m-n/(x)+1)
 #define ls p<<1
 #define rs p<<1|1

 const ll MOD=,inv2=(MOD+)/;
       double eps=1e-;
       ll INF=1e14;

 int read()
 {
    int v=,f=;
    char c=getchar();
    while(c<||<c) {if(c=='-') f=-; c=getchar();}
    while(<=c&&c<=) v=(v<<)+v+v+c-,c=getchar();
    return v*f;
 }

 int prime(ll x)
 {
     ll t=sqrt(x);
     for(ll i=;i<=t;i++)
      if(x%i==) return ;
     return ;
 }

 ll mult(ll a,ll b,ll p)
 {
     ll t=(a*b-ll((long double)a/p*b+1e-)*p)%p;
     return t<?t+p:t;
 }

 ll pw(ll x,ll y,ll p)
 {
     ll t=;
     while(y)
     {
         if(y&) t=mult(t,x,p);
         x=mult(x,x,p);
         y>>=;
     }
     return t;
 }

 int main()
 {
     //freopen("1.in","r",stdin);
     //freopen("1.out","w",stdout);
     int cas=read();
     while(cas--)
     {
         ll n;
         scanf("%I64d",&n);
         ll k=n-;
         if(n==) k=;
          else
          {
             while(k&&!prime(k)) k-=;
          }
         ll ans=n-;
         //printf("k=%I64d\n",k);
         for(ll i=k+;i<=n-;i++)
         {
             //printf("i=%I64d\n",i);
             ll t=pw(i,n-,n);
             //printf("inv%I64d=%I64d\n",i,t);
             ans=mult(ans,t,n);
         }

         printf("%I64d\n",ans);
     }
     return ;
 }