redhat本地yum源配置
/dev/sr0是光驱的设备名,/dev/cdrom代表光驱
/dev/sr0 与/dev/cdrom

/dev/cdrom 只是一个到sr0的符号链接
mount /dev/sr0 /mnt 挂载
umount /dev/sr0 /mnt 卸载
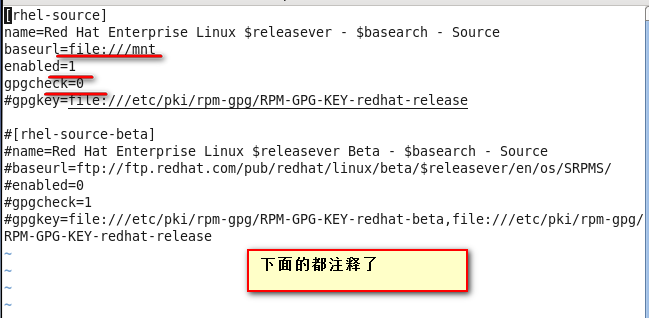
vi /etc/yum.repos.d/rhel-rource.repos
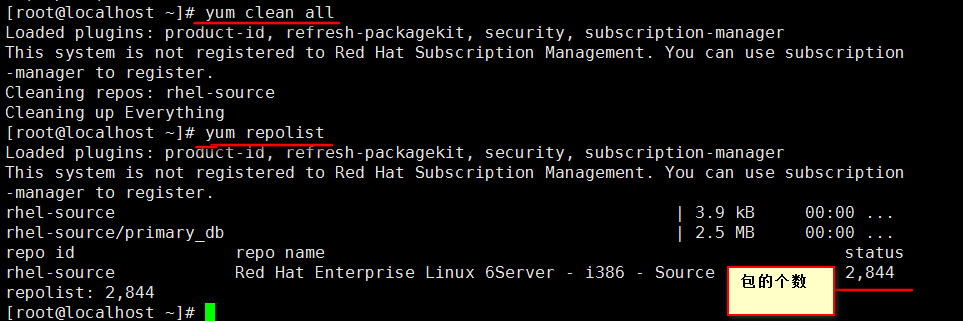
yum list
redhat本地yum源配置的更多相关文章
- RedHat和CentOS使用本地yum源配置
2013-04-01 11:38:30 标签:本地yum源 版权声明:原创作品,谢绝转载!否则将追究法律责任. 使用yum命令安装所需的软件,如果设备网络状况很好,当然也没必要去配置本地yum源,直接 ...
- Centos6.4 本地yum源配置
由于单位的服务器均使用的是内网,而安装一些软件如Git,需要很多的依赖包,使用yum安装相对简单,由于不能联网故配置本地yum源配置. 1.首先将需要rpm库添加到系统中: 1).虚拟机中安装的lin ...
- CentOS7利用本地yum源配置NBD
一:CentOS7.0创建本地YUM源 (物理机:直接将刻录的CentOS7光盘利用光驱插入物理机上) (虚拟机: CD/DVD>>连接本地ISO) 针对物理机192.168.9.112进 ...
- CENTOS 6-7的本地YUM源配置
本文档适合CENTOS 6-7的本地YUM源配置 cd /media cd CentOS_6.8_Final/ cd Packages 创建目录拷贝文件 mkdir /yum cp * /yum 配置 ...
- 企业级本地yum源配置方案详解
因目前企业生产网络禁止联网,对于使用Linux的我们来说,非常不方便,想要使用yum源都很困难,挂dvd又不能完全满足要求,所以自建一个企业级的yum源,定时从公网同步到本地,然后生产网络直接配置在本 ...
- CentOS 6.x 本地yum源配置与使用
系统默认已经安装了可使用yum的软件包,所以可以直接配置: # mount /dev/cdrom /mnt 挂载镜像,可以写到配置文件 ...
- CentOS本地yum源配置
现有一台处在局域网的linux服务器,无法ping通外网,本文是关于本地yum源的配置 环境 : CentOS 6.5 一 .挂载CentOS镜像文件 (1) 创建挂载文件夹,若此文件夹已存在可忽略 ...
- Linux本地yum源配置以及使用yum源安装gcc编译环境
本文档是图文安装本地yum源的教程,以安装gcc编译环境为例. 适用范围:所有的cetos,红帽,fedroa版本 适用人群:有一点linux基础的小白 范例系统版本:CentOS Linux rel ...
- RHEL7 本地yum源配置
配置yum 源 1.挂载DVD光盘到/mnt 因为配置时候路径名里面不能有空格,否则不能识别 [root@ mnt]# mount /dev/cdrom /mnt 2.在目录/etc/yum.r ...
随机推荐
- Daily Scrum - 11/19
今天任烁帮忙更新了大家在Sprint 2中的Task,基本每人的Task都是细分到每天的,这样大家初期的工作应该会更有效率一点. 任烁今天表示“进度条背词法”应该是可以融合到原有算法中的,期待他的改进 ...
- ElasticSearch 2 (25) - 语言处理系列之同义词
ElasticSearch 2 (25) - 语言处理系列之同义词 摘要 词干提取有助于通过简化屈折词到它们词根的形式来扩展搜索的范围,而同义词是通过关联概念和想法来扩展搜索范围的.或许没有文档能与查 ...
- Jmeter使用笔记之意料之外的
以下是在测试过程中按照以前loadrunner的思维来做的一点区别: 一.组织方式之setup 在用loadrunner做接口测试的时候如果不是针对login的测试,那么一般也会把login接口放到i ...
- Python面向对象高级编程:@property--把方法变为属性
为了限制score的范围,可以通过一个set_score()方法来设置成绩,再通过一个get_score()来获取成绩,这样,在set_score()方法里,就可以检查参数: >>> ...
- Magical Girl Haze 南京网络赛2018
题意: 就是使不大于k条路的权值变为零后求最短路 解析: d[i][j]表示使j条路变为权值后从起点到点i的最短路径 这题不能用spfa做 tle #include <iostream> ...
- Fire Net HDU - 1045(二分匹配)
把每一列中相邻的 . 缩为一个点 作为二分图的左边 把每一行中相邻的 . 缩为一个点 作为二分图的右边 然后求最大匹配即可 这题用匈牙利足够了...然而..我用了hk...有点大材小用的感觉// ...
- 【刷题】BZOJ 2125 最短路
Description 给一个N个点M条边的连通无向图,满足每条边最多属于一个环,有Q组询问,每次询问两点之间的最短路径. Input 输入的第一行包含三个整数,分别表示N和M和Q 下接M行,每行三个 ...
- Fib的奇怪定理 : gcd(F[n],F[m])=F[gcd(n,m)]
引理1:gcd(F[n],f[n-1])=1 因为 F[n]=f[n-1]+F[n-2] 所以 gcd(F[n],f[n-1]) = gcd(F[n-1]+F[n-2],F[n-1]) gcd的更损相 ...
- 洛谷 P2303 [SDOi2012]Longge的问题 解题报告
P2303 [SDOi2012]Longge的问题 题目背景 SDOi2012 题目描述 Longge的数学成绩非常好,并且他非常乐于挑战高难度的数学问题.现在问题来了:给定一个整数\(N\),你需要 ...
- 函数、可变参数、keyword-only参数、实参解构
函数的数学定义:y=f(x) ,y是x的函数,x是自变量.y=f(x0, x1, ..., xn) python中的函数: 由函数名称.参数列表.和若干语句组成的语句块构成,完成一定的功能,是组织代码 ...
