隐马尔科夫模型研究 stock 以及 lotto
说明
本文参考了这里
由于数据是连续的,因此使用了高斯隐马尔科夫模型:gaussianHMM
一、stock代码
import tushare as ts
import pandas as pd
import numpy as np
from hmmlearn.hmm import GaussianHMM
from matplotlib import cm, pyplot as plt
import seaborn as sns
sns.set_style('white')
'''
假定隐藏状态数目为4,观测状态数目为2
'''
# 1.准备 X
df = ts.get_hist_data('sh',start='2014-01-01',end='2017-07-27')[::-1] # 上证指数
close = np.log(df['close'])
low, high = np.log(df['low']), np.log(df['high'])
t = 5
X = pd.concat([close.diff(1), close.diff(t), high-low], axis=1)[t:] # 显状态时间序列(观测得到)
# 2.拟合 HMM
model = GaussianHMM(n_components=6, covariance_type="diag", n_iter=1000).fit(X)
Z = model.predict(X) # 隐状态时间序列
# 3.画图看看
plt.figure(figsize=(12, 7))
for i in range(model.n_components):
mask = (Z==i) # 注意这里的Z!!!
plt.plot_date(df.index[t:][mask], df['close'][t:][mask],'.',label=f'{i}th hidden state',lw=1)
plt.legend()
plt.grid(1)
plt.show()
效果图
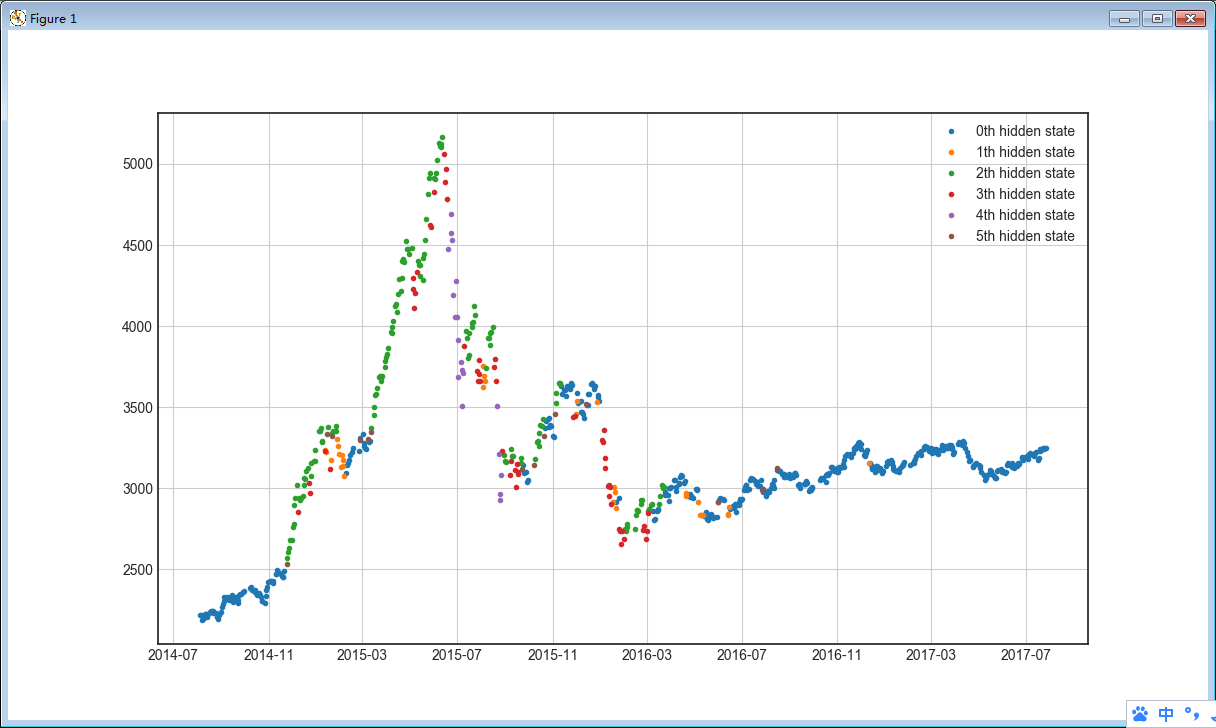
解释
下面是对6种隐状态的一种可能的解释:【图文对不上,文字来自这里】
- 状态0————蓝色————震荡下跌
- 状态1————绿色————小幅的上涨
- 状态2————红色————牛市上涨
- 状态3————紫色————牛市下跌
- 状态4————黄色————震荡下跌
- 状态5————浅蓝色————牛市下跌
以上的意义归结是存在一定主观性的。因为HMM模型对输入的多维度观测变量进行处理后,只负责分出几个类别,而并不会定义出每种类别的实际含义。所以我们从图形中做出上述的判断。
所以,这种方法本质上是一种 Classification(分类) 或者 Clustering(聚类)
二、lotto 代码
import tushare as ts
import pandas as pd
import numpy as np
from hmmlearn.hmm import GaussianHMM
from matplotlib import cm, pyplot as plt
from matplotlib.widgets import MultiCursor
import seaborn as sns
sns.set_style('white')
import marksix_1
import talib as ta
'''
假定隐藏状态数目为6,观测状态数目为4
'''
# 1.准备 X
lt = marksix_1.Marksix()
lt.load_data(period=1000)
#series = lt.adapter(loc='0000001', zb_name='ptsx', args=(1,), tf_n=0)
m = 2
series = lt.adapter(loc='0000001', zb_name='mod', args=(m, lt.get_mod_list(m)), tf_n=0)
# 实时线
close = np.cumsum(series).astype(float)
# 低阶数据
t1, t2, t3 = 5, 10, 20
ma1 = ta.MA(close, timeperiod=t1, matype=0)
std1 = ta.STDDEV(close, timeperiod=t1, nbdev=1)
ma2 = ta.MA(close, timeperiod=t2, matype=0)
std2 = ta.STDDEV(close, timeperiod=t2, nbdev=1)
ma3 = ta.MA(close, timeperiod=t3, matype=0)
std3 = ta.STDDEV(close, timeperiod=t3, nbdev=1)
# 转换一
'''
t = t3
X = pd.DataFrame({'ma1':ma1,'ma2':ma2,'ma3':ma3,'std1':std1,'std2':std2,'std3':std3}, index=lt.df.index)[t:]
'''
# 转换二
t = t2
X = pd.DataFrame({'ma1':ma1,'ma2':ma2,'std1':std1,'std2':std2}, index=lt.df.index)[t:]
#close = np.log(df['close'])
#low, high = np.log(df['low']), np.log(df['high'])
#t = 5
#X = pd.concat([close.diff(1), close.diff(t), high-low], axis=1)[t:] # 显状态时间序列(观测得到)
# 2.拟合 HMM
model = GaussianHMM(n_components=6, covariance_type="diag", n_iter=1000).fit(X)
Z = model.predict(X) # 隐状态时间序列
# 3.画图看看
fig, axes = plt.subplots(2, 1, sharex=True)
ax1, ax2 = axes[0], axes[1]
show_period = 300
# 布林线
upperband, middleband, lowerband = ta.BBANDS(close, timeperiod=5, nbdevup=2, nbdevdn=2, matype=0)
axes[0].plot_date(lt.df.index[-show_period:], close[-show_period:], 'rd-', markersize = 3)
axes[0].plot_date(lt.df.index[-show_period:], upperband[-show_period:], 'y-')
axes[0].plot_date(lt.df.index[-show_period:], middleband[-show_period:], 'b-')
axes[0].plot_date(lt.df.index[-show_period:], lowerband[-show_period:], 'y-')
for i in range(model.n_components):
mask = (Z[-show_period:]==i) # 注意这里的Z!!!
axes[1].plot_date(lt.df.index[-show_period:][mask], close[-show_period:][mask],'d',markersize=3,label=f'{i}th hidden state',lw=1)
axes[1].legend()
axes[1].grid(1)
multi = MultiCursor(fig.canvas, (axes[0], axes[1]), color='b', lw=2)
plt.show()
效果图
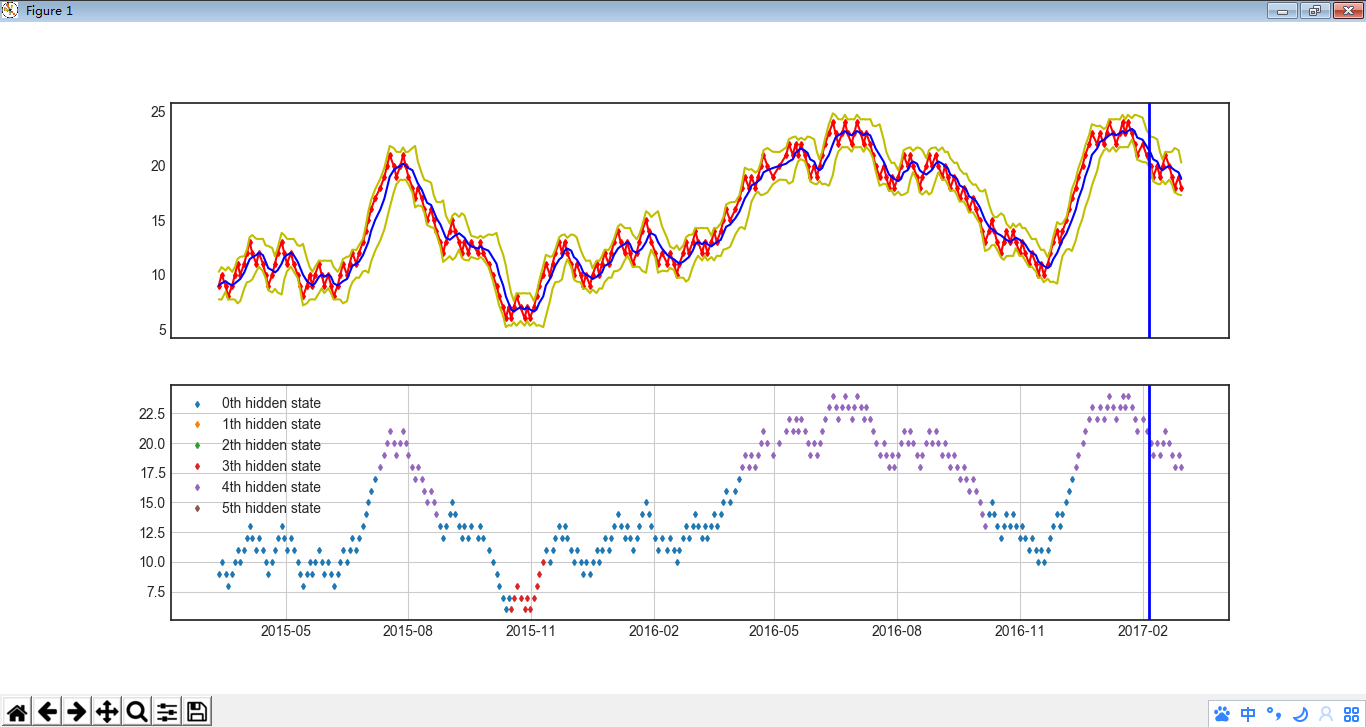
隐马尔科夫模型研究 stock 以及 lotto的更多相关文章
- HMM基本原理及其实现(隐马尔科夫模型)
HMM(隐马尔科夫模型)基本原理及其实现 HMM基本原理 Markov链:如果一个过程的“将来”仅依赖“现在”而不依赖“过去”,则此过程具有马尔可夫性,或称此过程为马尔可夫过程.马尔可夫链是时间和状态 ...
- 基于隐马尔科夫模型(HMM)的地图匹配(Map-Matching)算法
文章目录 1. 1. 摘要 2. 2. Map-Matching(MM)问题 3. 3. 隐马尔科夫模型(HMM) 3.1. 3.1. HMM简述 3.2. 3.2. 基于HMM的Map-Matchi ...
- 隐马尔科夫模型HMM学习最佳范例
谷歌路过这个专门介绍HMM及其相关算法的主页:http://rrurl.cn/vAgKhh 里面图文并茂动感十足,写得通俗易懂,可以说是介绍HMM很好的范例了.一个名为52nlp的博主(google ...
- 隐马尔科夫模型HMM(三)鲍姆-韦尔奇算法求解HMM参数
隐马尔科夫模型HMM(一)HMM模型 隐马尔科夫模型HMM(二)前向后向算法评估观察序列概率 隐马尔科夫模型HMM(三)鲍姆-韦尔奇算法求解HMM参数(TODO) 隐马尔科夫模型HMM(四)维特比算法 ...
- 隐马尔科夫模型(Hidden Markov Models)
链接汇总 http://www.csie.ntnu.edu.tw/~u91029/HiddenMarkovModel.html 演算法笔记 http://read.pudn.com/downloads ...
- 隐马尔科夫模型HMM
崔晓源 翻译 我们通常都习惯寻找一个事物在一段时间里的变化规律.在很多领域我们都希望找到这个规律,比如计算机中的指令顺序,句子中的词顺序和语音中的词顺序等等.一个最适用的例子就是天气的预测. 首先,本 ...
- 隐马尔科夫模型(HMM)
基本概念 1Markov Models 2Hidden Markov Models 3概率计算算法前向后向算法 1-3-1直接计算 1-3-2前向算法 1-3-3后向算法 4学习问题Baum-Welc ...
- 机器学习中的隐马尔科夫模型(HMM)详解
机器学习中的隐马尔科夫模型(HMM)详解 在之前介绍贝叶斯网络的博文中,我们已经讨论过概率图模型(PGM)的概念了.Russell等在文献[1]中指出:"在统计学中,图模型这个术语指包含贝叶 ...
- 隐马尔科夫模型 HMM(Hidden Markov Model)
本科阶段学了三四遍的HMM,机器学习课,自然语言处理课,中文信息处理课:如今学研究生的自然语言处理,又碰见了这个老熟人: 虽多次碰到,但总觉得一知半解,对其了解不够全面,借着这次的机会,我想要直接搞定 ...
随机推荐
- SVN switch 用法总结
一直知道SVN有个switch命令,但是对它的介绍教程却很少,大多是生硬的svn帮助文档里的文字,从而一直不怎么会用.今天看了这篇文章,突觉豁然开朗,整理下来以备查阅. 使用SVN,自然是需要与别人合 ...
- LeetCode题解之Climbing Stairs
1.题目描述 2.问题分析 使用动态规划. 3.代码 int climbStairs(int n) { ){ return n; } ]; dp[] = ; dp[] = ; dp[] = ; ; i ...
- 虚拟机压力测试延迟高的可能原因及 ILPIP 配置 / 查询脚本
测试初期 Client VM 的延迟结果正常: 测试后期 Client VM 的延迟偶尔突增/连接失败,越后期超高延迟(比如 30 秒)出现越多: 问题分析 造成这一现象的根本原因很可能是 SNAT( ...
- 使用动态跟踪技术SystemTap监控MySQL、Oracle性能
[IT168 技术]本文根据吕海波2018年5月11日在[第九届中国数据库技术大会]上的演讲内容整理而成. 讲师介绍: 吕海波,美创科技研究员,ITPUB管理版版主.出版技术书籍<Oracle内 ...
- HTTP的cookie
HTTP cookies,通常又称作"cookies",已经存在了很长时间,但是仍旧没有被予以充分的理解.首要的问题是存在了诸多误区,认为cookies是后门程序或病毒,或压根不知 ...
- Linux之JDK1.8的安装
这个最基础的,但是老是查了一次又查,干脆记起来吧. 一.下载jdk8 地址:http://www.oracle.com/technetwork/java/javase/downloads/index. ...
- 解决:Windows 强制升级为8.1之后 Mysql连接不上, VisualSVN Server无服务
1.mysql 连不上,只要将mysql重新加为windows服务即可.(我的是mysql-5.6.24-winx64 解压版) 方法:mysqld --install mysql --defa ...
- 某某D的手伸的实在太长了,路由器也未能幸免,致被阉割的TP-Link
前段时间整了个服务器架上l2tp.server, TP-Link路由连上去后,全网走l2tp通道,而且不能配置相关的路由表 然后研究啊 找啊 查啊,确定是路由没有这功能 找客服问了一下,他一听就懂了, ...
- cJSON 使用详解
由于c语言中,没有直接的字典,字符串数组等数据结构,所以要借助结构体定义,处理json.如果有对应的数据结构就方便一些, 如python中用json.loads(json)就把json字符串转变为内建 ...
- 团队作业——Alpha冲刺 1/12
团队作业--Alpha冲刺 Alpha 阶段认领的任务 杨光海天:加入随心摘首页和编辑界面的开发中,并完成冲刺博文的撰写 郭剑南.周琪文:图像识别核心算法的实现 赖志平:随心摘首页和编辑界面开发主力, ...
