IntelliJ IDEA 2017安装和破解方法

一，安装

这里是windows下的安装，另外还有mac和linux下的版本，可自行解决

下载并安装IDEA
官网：https://www.jetbrains.com/idea/

或者百度网盘2017版本的：

前提：确定安装了jdk1.8版本以上，并且配置好了java的环境。

jdk的版本选择：几个版本什么区别

1、点击安装，选择你要安装的路径

2、根据你的系统选择安装的位数，如下图所示：

这里下面是否关联.java和.groovy等文件，这里不建议勾选，应该让它关联更加轻量级的查看工具，如notepad++。

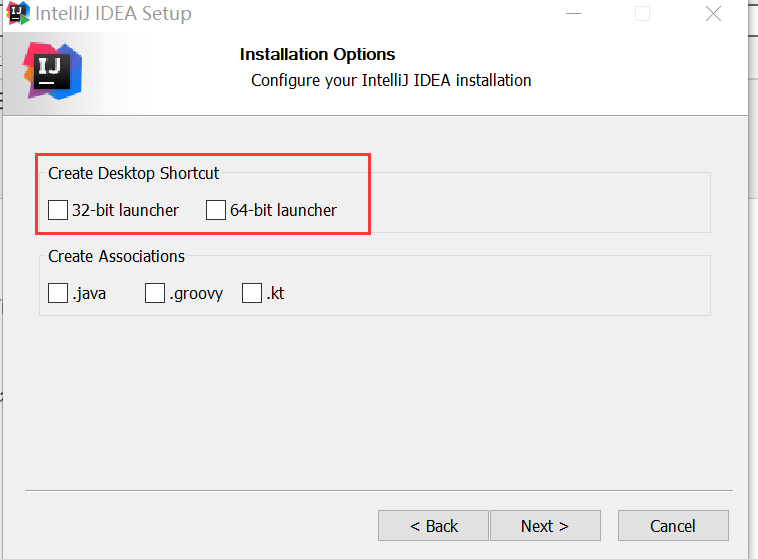
3、下面选择目录文件夹，采用默认的Jetbrains就行。

4、然后点击install安装，直到安装成功。

二、破解

1、下载破解补丁
地址：https://pan.baidu.com/s/1ld89X-4X3p7r5X-FThnSHw 密码：l4t7

2、空手去破解，修改补丁的路径。
将下载的文件放到安装IDEA路径的bin目录下（如图），然后找到如下图的两个文件，

找到idea.exe.vmoptions和idea64.exe.vmoptions，用notepad++（或记事本）打开它们。

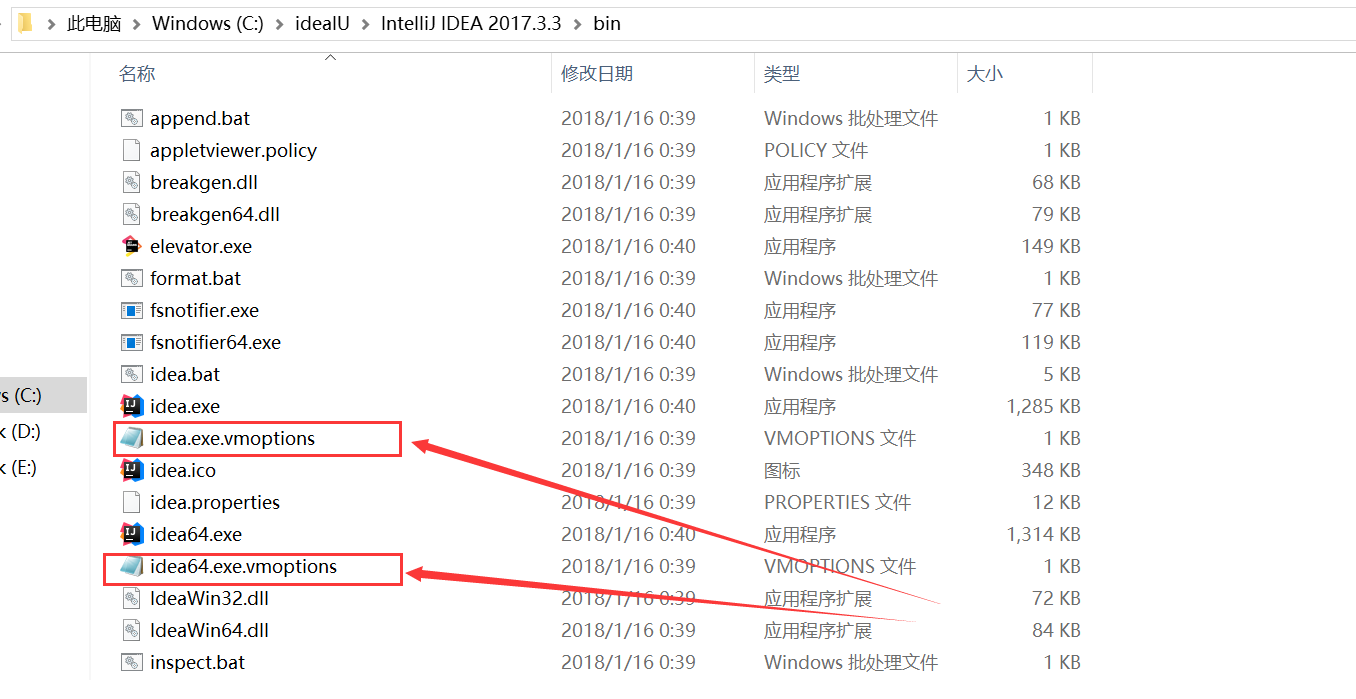
然后在这两个文件的最后都加上如下代码：（注意，其实这里是要修改破解补丁的路径，一定要按照自己的路径来。）

-javaagent:C:\Program Files\JetBrains\IntelliJ IDEA 2017.3.3\bin\JetbrainsCrack-2.10-release-enc.jar

-javaagent:C:\Program Files\JetBrains\IntelliJ IDEA 2017.3.3\bin\JetbrainsCrack-2.10-release-enc.jar

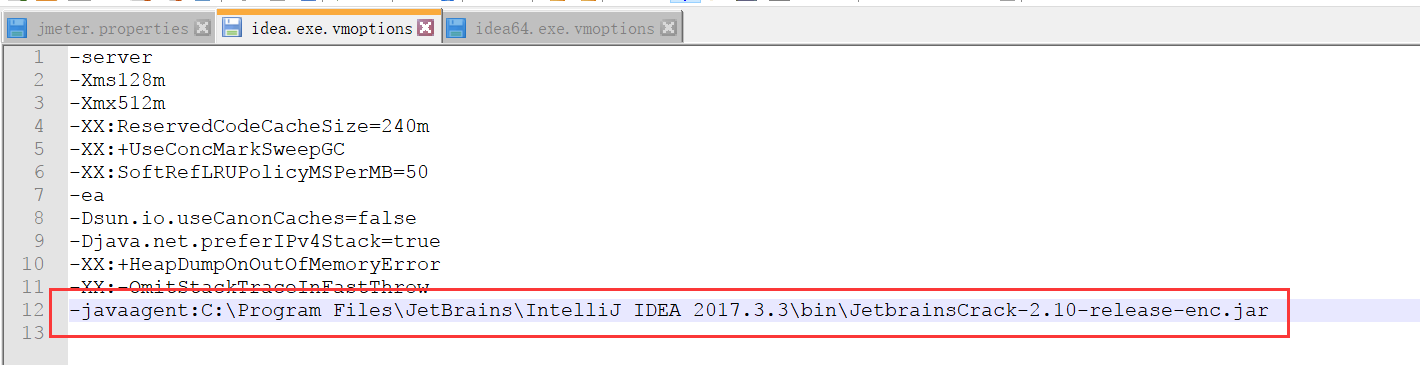
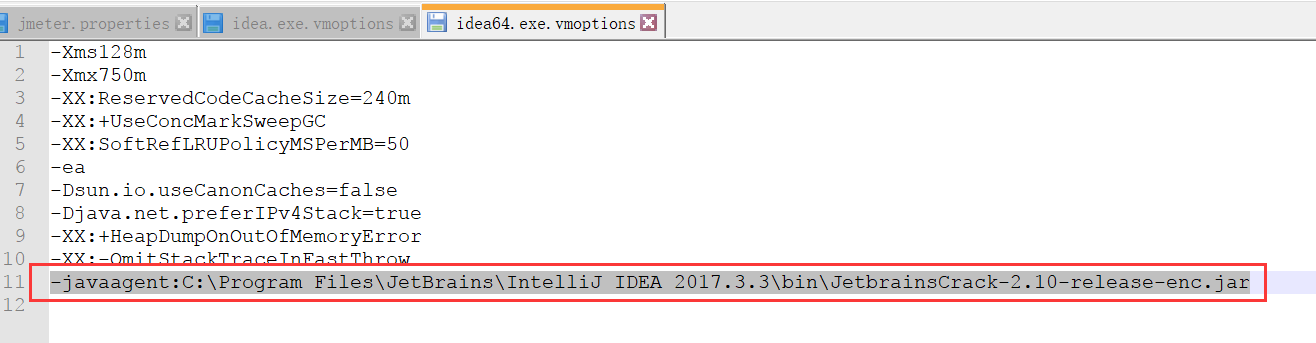
3、修改Activation code

重启Intellij IDEA ,在Activation code输入：

 ThisCrackLicenseId-{
 "licenseId":"ThisCrackLicenseId",
 "licenseeName":"你想要的用户名",
 "assigneeName":"",
 "assigneeEmail":"随便填一个邮箱(我填的:idea@163.com)",
 "licenseRestriction":"For This Crack, Only Test! Please support genuine!!!",
 "checkConcurrentUse":false,
 "products":[
 {"code":"II","paidUpTo":"2099-12-31"},
 {"code":"DM","paidUpTo":"2099-12-31"},
 {"code":"AC","paidUpTo":"2099-12-31"},
 {"code":"RS0","paidUpTo":"2099-12-31"},
 {"code":"WS","paidUpTo":"2099-12-31"},
 {"code":"DPN","paidUpTo":"2099-12-31"},
 {"code":"RC","paidUpTo":"2099-12-31"},
 {"code":"PS","paidUpTo":"2099-12-31"},
 {"code":"DC","paidUpTo":"2099-12-31"},
 {"code":"RM","paidUpTo":"2099-12-31"},
 {"code":"CL","paidUpTo":"2099-12-31"},
 {"code":"PC","paidUpTo":"2099-12-31"}
 ],
 "hash":"2911276/0",
 "gracePeriodDays":7,
 "autoProlongated":false}

4、修改完之后能够进入下一个界面说明破解成功。

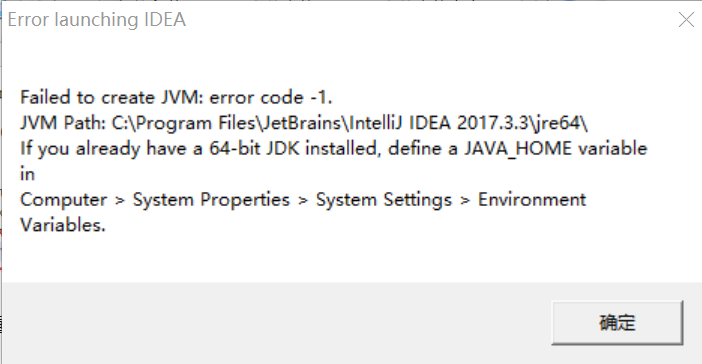
**【安装过程遇到的坑：修改完文件重启idea时提示：不能创建jvm】

1、我出现这个问题的原因是补丁的路径前面的参数忘记写了：-javaagent: 一定要检查好呀。