hdu 6441 Find Integer(费马大定理+勾股数)

题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=6441(本题来源于2018年中国大学生程序设计竞赛网络选拔赛)

题意:输入n和a，求满足等式a^n+b^n=c^n的b，c的值

思路:

首先我们要知道什么是费马大定理

百度词条

费马大定理，又被称为“费马最后的定理”，由17世纪法国数学家皮耶·德·费马提出。

他断言当整数n >2时，关于x, y, z的方程 x^n + y^n = z^n 没有正整数解。

德国佛尔夫斯克曾宣布以10万马克作为奖金奖给在他逝世后一百年内，第一个证明该定理的人，吸引了不少人尝试并递交他们的“证明”。

被提出后，经历多人猜想辩证，历经三百多年的历史，最终在1995年被英国数学家安德鲁·怀尔斯彻底证明。

 

因此，只需讨论n=1，n=2两种情况，其余的n值直接输出"-1 -1"

①n=1

等式相当于a+b=c，直接输出"1 a+1"

②n=2

等式相当于a^2+b^2=c^2，此时需要探索勾股数奇偶性的规律(原文链接:https://wenku.baidu.com/view/8282f1b669eae009591bec85.html)

 

 

A.当勾(a)为奇数时

a.列表

b.归纳规律

（1）每组中a都是奇数

c.证明

 

B.当a(勾)为偶数时

a.列表

b.归纳规律

（1）每组中a(勾)是偶数，(第一组较特殊，勾比股大)

c.证明

由上可以总结出奇偶数列法则

定理:如a^2+b^2=c^2是直角三角形的三个整数边长，则必有如下a值的奇数列、偶数列关系成立；
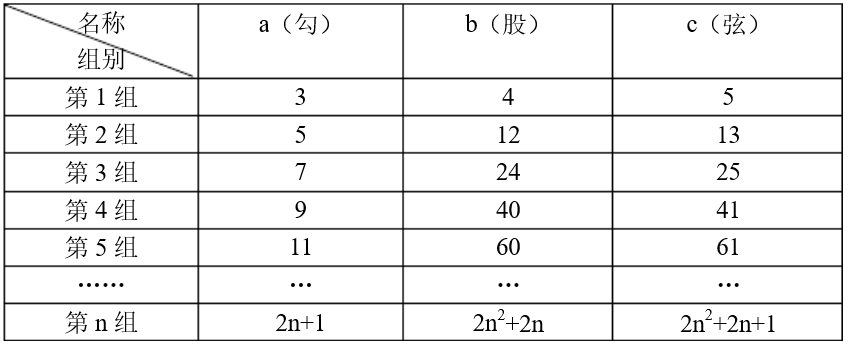
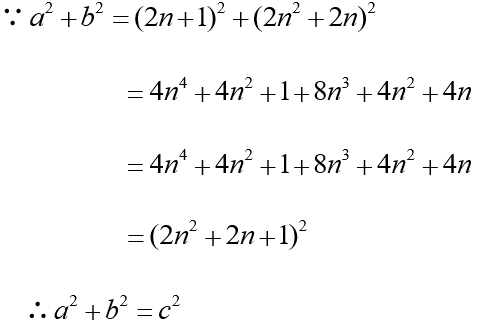
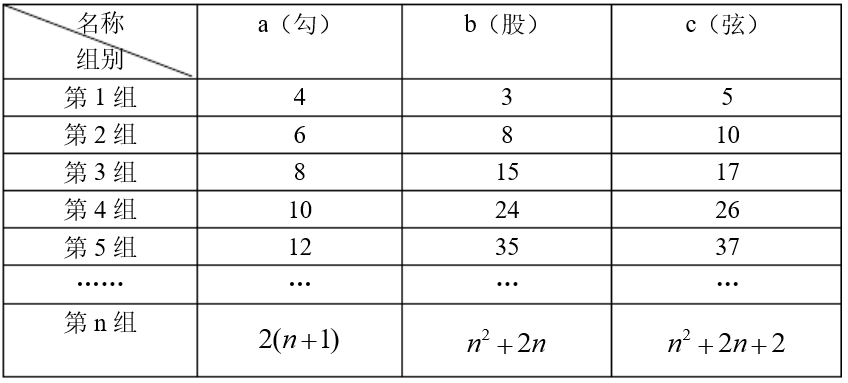
(一)直角三角形a^2+b^2=c^2的奇数列a法则 
若a为2n+1型奇数,则a为奇数列平方整数解的关系是：

a=2n+1　　b=n^2+(n+1)^2-1　　c=n^2+(n+1)^2

(二)直角三角形a^2+b^2=c^2的偶数列a法则：

若a为2n型偶数,则a为偶数列平方整数解的关系是：

a= 2n+2　　b=n^2+2n　　c=n^2+2n+2

 

标准程序:

 #include<bits/stdc++.h>
 using namespace std;
 int main()
 {
     long long n,a,z,i;
     scanf("%lld",&i);
     while(i--)
     {
         scanf("%lld%lld",&n,&a);
         if(n==)
             printf("1 %lld\n",a+);
         else if(n==)
         {
             z=a*a;
             if(a%==)
             {
                 z=z/;
                 printf("%lld %lld",z,z+);
             }
             else if(a%==)
             {
                 z=z/;
                 printf("%lld %lld\n",z-,z+);
             }
         }
         else printf("-1 -1\n");
     }
     return ;
 }