vue工厂化完整项目目录
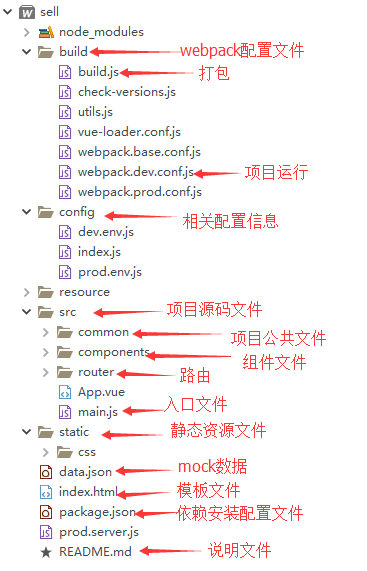
vue工厂化完整项目目录的更多相关文章
- vue中的项目目录assets和staitc的区别
vue中的项目目录assets和staitc的区别 在进行发行正式版时,即为npm run build编译后, assets下的文件如(js.css)都会在dist文件夹下面的项目目录分别合并到一个文 ...
- vue构建完整项目-以及实现
简介 由于开发vue项目的时候,需要重新搭建项目的架子,比较麻烦,其实之前做过的项目好多都可以直接拿过来用,比如接下来的这个项目,就可以满足平常的vue单页面开发. 该项目包括了: 全局配置axios ...
- 【vue】项目目录结构及使用多的知识点
项目目录: Node_modules/npm安装的该项目的依赖库 vuex/文件夹存放的是和 Vuex store 相关的东西(state对象,actions,mutations) router/文件 ...
- Vue之vue自动化工具快速搭建单页项目目录
1 生成项目目录 使用vue自动化工具可以快速搭建单页应用项目目录. 该工具为现代化的前端开发工作流提供了开箱即用的构建配置.只需几分钟即可创建并启动一个带热重载.保存时静态检查以及可用于生产环境的构 ...
- vue项目目录介绍
Vue项目目录 初始化项目 vue init webpack []projectname] cd [projectname] npm install vue run dev 目录树 +---build ...
- vue项目目录结构
VUE项目目录结构 如上图所示,我们的目录结构就是这样的了. 目录/文件 说明 build 这个是我们最终发布的时候会把代码发布在这里,在开发阶段,我们基本不用管. config 配置目录,默认配置没 ...
- vue项目目录
项目目录说明 . |-- config // 项目开发环境配置 | |-- index.js // 项目 ...
- 【vue iview】项目 win10 放在C盘 经常npm install不成功,就是因为 权限问题,把代码目录放到D盘就没事了。
[vue iview]项目 win10 放在C盘 经常npm install不成功,就是因为 权限问题,把代码目录放到D盘就没事了.
- Vue框架(三)——Vue项目搭建和项目目录介绍、组件、路由
Vue项目环境搭建 1) 安装node,在官网下载好,然后在本地安装 官网下载安装包,傻瓜式安装:https://nodejs.org/zh-cn/ 2) 换源安装cnpm >: npm ins ...
随机推荐
- 超线程技术——超线程技术让(P4)处理器增加5%的裸晶面积,就可以换来15%~30%的效能提升,本质单核模拟双核!和异步编程的思想无异。
超线程是Intel 所研发的一种技术,于2002年发布.超线程的英文是HT技术,全名为Hyper-Threading,中文又名超线程.超线程技术原先只应用于Intel Xeon处理器中,当时称为Sup ...
- 【415】C语言文件读写
A program can open and close, and read from, and write to, a file that is defined by the user This i ...
- E20180218-hm-xa
更新: 2019/02/19 原来忘记分类,把此博文归入单词类 vocabulary n. (某一语言的) 词汇; (尤指外语教科书中附有释义的) 词汇表; grammar n. 语法; 语法书; ...
- 洛谷 P4016 负载平衡问题 【最小费用最大流】
求出平均数sum,对于大于sum的点连接(s,i,a[i]-sum,0),表示这个点可以流出多余的部分,对于小于sum的点连接(i,t,sum-a[i],0)表示这个点可以接受少的部分,然后每个点向相 ...
- NOIp 2014 联合权值 By cellur925
题目传送门 这题自己(真正)思考了很久(欣慰). (轻而易举)地发现这是一棵树后,打算从Dfs序中下功夫,推敲了很久规律,没看出来(太弱了). 开始手动枚举距离为2的情况,模模糊糊有了一些概念,但没有 ...
- jQuery笔记之data方法
成品图如下所示: 搭建HTML+CSS结构 <style> /* 给tpl设置为不可见,因为我们不需要用到他,我们只是要克隆他身上的东西,克隆完就把他删掉.就跟渣男一样!!!*/ .tpl ...
- 【CSS】少年,你想拥有写轮眼么?
最近笔者在公司内部开展了一次CSS讲座,由于授课经验不太足,授课效果自我感觉并不太好,不过课中有一个笔者用CSS写的一个小效果,其中还是包含了蛮多CSS的常见知识点的,正好也有部分同学很感兴趣如何实现 ...
- IDEA远程调试Tomcat程序
如何使用 Idea 远程调试 Java 代码 IDEA远程调试的 基本就是在服务端先设置Tomcat服务器启动脚本catalina.bat,然后在客户端IDEA上进行参数配置,最后二者可以通过Sock ...
- QT5每日一学(三) QT登陆对话框
一.使用设计模式创建界面 1.新建Qt Widgets Application,项目名称为login,类名和基类保持MainWindow和QMainWindow不变. 2.完成项目创建后,向项目中添加 ...
- 题解报告:hdu 1408 盐水的故事
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=1408 Problem Description 挂盐水的时候,如果滴起来有规律,先是滴一滴,停一下:然后 ...
