士兵杀敌 三 --- O( 1 ) 的时间复杂度 .

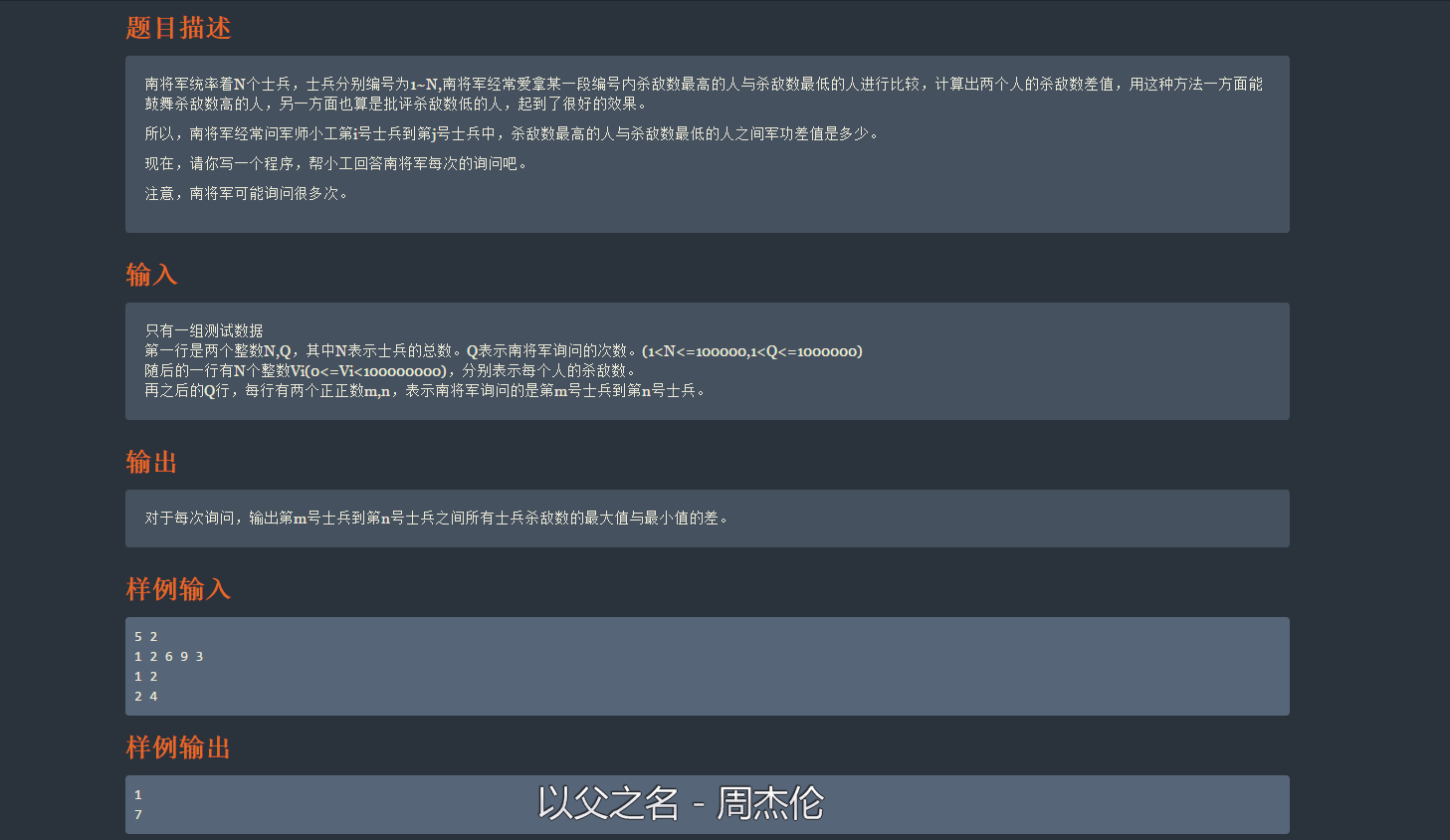
一看就是 十分简单的  题  ,   然后上去开始无脑程序

超时~~~      感觉时间复杂度 , 已经很低了  ,  但是并没有什么卵用 .

 #include<stdio.h>
 #include<string.h>
 #include<math.h>
 #include<iostream>
 #include<algorithm>
 #include<queue>
 #include<vector>
 #include<set>
 #include<stack>
 #include<string>
 #include<sstream>
 #include<map>
 #include<cctype>
 #include<limits.h>
 using namespace std;
 int main()
 {
     int w,q,a[],n,m;
     scanf("%d%d",&w,&q);
     for(int i=;i<=w;i++)
         scanf("%d",&a[i]);
     for(int i=;i<q;i++)
     {
         int maxn=INT_MIN,minn=INT_MAX;
         scanf("%d%d",&n,&m);
         for(int j=n;j<=m;j++)
         {
             maxn=maxn>a[j]?maxn:a[j];
             minn=minn<a[j]?minn:a[j];
         }
         printf("%d\n",maxn-minn);
     }
     return ;
 }

两个程序的时间复杂度

 #include<stdio.h>
 #include<string.h>
 #include<math.h>
 #include<iostream>
 #include<algorithm>
 #include<queue>
 #include<vector>
 #include<set>
 #include<stack>
 #include<string>
 #include<sstream>
 #include<map>
 #include<cctype>
 #include<limits.h>
 using namespace std;
 int dp_max[][];
 int dp_min[][];
 void RMQ(int n)
 {
     for(int j = ; j < ; j++)     //   这里 为啥 是 20 呢  ? //F[i, j]表示从第i个数起连续2^j个数中的最大值。（DP的状态） ???
     {
         for(int i = ; i <= n; i++)
         {
             if( i + (<<j)- <= n)
             {
                 dp_max[i][j] = max(dp_max[i][j-],dp_max[i+(<<(j-))][j -]);
                 dp_min[i][j] = min(dp_min[i][j-],dp_min[i+(<<(j-))][j-]);
             }
         }
     }
 }
 int main()
 {
     int n,q,m,k;
     scanf("%d%d",&n,&q);            //   士兵的 总人数  .
     for(int i = ; i <= n; i++)
     {
         scanf("%d",&dp_max[i][]);      //
         dp_min[i][]=dp_max[i][];    //    最小和最大 都先默认了
     }
     RMQ(n);             //   一共 有  n  个 数字
     while(q--)
     {
         scanf("%d%d",&m,&k);
         int s=(int)(log(k-m+)/log());
         int max_val = max(dp_max[m][s],dp_max[k-(<<s)+][s]);
         int min_val = min(dp_min[m][s],dp_min[k-(<<s)+][s]);
         printf("%d\n",max_val - min_val);
     }
     return ;
 }