codeforces 696C C. PLEASE(概率+快速幂)

题目链接：

C. PLEASE

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

As we all know Barney's job is "PLEASE" and he has not much to do at work. That's why he started playing "cups and key". In this game there are three identical cups arranged in a line from left to right. Initially key to Barney's heart is under the middle cup.

Then at one turn Barney swaps the cup in the middle with any of other two cups randomly (he choses each with equal probability), so the chosen cup becomes the middle one. Game lasts n turns and Barney independently choses a cup to swap with the middle one within each turn, and the key always remains in the cup it was at the start.

After n-th turn Barney asks a girl to guess which cup contains the key. The girl points to the middle one but Barney was distracted while making turns and doesn't know if the key is under the middle cup. That's why he asked you to tell him the probability that girl guessed right.

Number n of game turns can be extremely large, that's why Barney did not give it to you. Instead he gave you an array a1, a2, ..., aksuch that

in other words, n is multiplication of all elements of the given array.

Because of precision difficulties, Barney asked you to tell him the answer as an irreducible fraction. In other words you need to find it as a fraction p / q such that 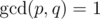, where  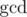is the greatest common divisor. Since p and q can be extremely large, you only need to find the remainders of dividing each of them by 10^9 + 7.

Please note that we want 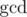 of p and q to be 1, not  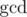of their remainders after dividing by 109 + 7.

Input

The first line of input contains a single integer k (1 ≤ k ≤ 10^5) — the number of elements in array Barney gave you.

The second line contains k integers a1, a2, ..., ak (1 ≤ ai ≤ 10^18) — the elements of the array.

Output

In the only line of output print a single string x / y where x is the remainder of dividing p by 109 + 7 and y is the remainder of dividing qby 109 + 7.

Examples

input

1
2

output

1/2

input

3
1 1 1

output

0/1

题意：

三个杯子,物品一开始在中间的杯子里,在n此交换后,问物品在中间的杯子里的概率;

思路：

可以先求出概率的表达式,可以得到一个表达式2*dp[n]+dp[n-1]=1;最后就是一个等比数列的和dp[n]=(2^(n-1)+(-1)^n)/(3*2^(n-1));
再看一下分子是否是3的倍数;然后就是快速幂对这个式子求结果了,中间要用费马小定理哟;

AC代码：

#include <bits/stdc++.h>
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>

using namespace std;

#define For(i,j,n) for(int i=j;i<=n;i++)
#define mst(ss,b) memset(ss,b,sizeof(ss));

typedef  long long LL;

template<class T> void read(T&num) {
    char CH; bool F=false;
    for(CH=getchar();CH<'0'||CH>'9';F= CH=='-',CH=getchar());
    for(num=0;CH>='0'&&CH<='9';num=num*10+CH-'0',CH=getchar());
    F && (num=-num);
}
int stk[70], tp;
template<class T> inline void print(T p) {
    if(!p) { puts("0"); return; }
    while(p) stk[++ tp] = p%10, p/=10;
    while(tp) putchar(stk[tp--] + '0');
    putchar('\n');
}

const LL mod=1e9+7;
const double PI=acos(-1.0);
const LL inf=1e18;
const int N=3e6+10;
const int maxn=3e6;
const double eps=1e-10;

int n;
LL a[N];

LL pow_mod(LL x,LL y,LL mod)
{
    LL s=1,base=x;
    while(y)
    {
        if(y&1)s=s*base%mod;
        base=base*base%mod;
        y>>=1;
    }
    return s;
}

int main()
{
        read(n);
        For(i,1,n)read(a[i]);
        LL temp=1;
        For(i,1,n)temp=a[i]%2*temp%2;
        int flag=0;
        if((pow_mod(2,(temp+1)%2,3)+pow_mod(-1,temp,3))%3==0)flag=1;
        LL p=1,q=1;
        temp=1;
        For(i,1,n)temp=a[i]%(mod-1)*temp%(mod-1);
        p=pow_mod(2,(temp-1+mod-1)%(mod-1),mod)+pow_mod(-1,temp,mod);
        if(flag)p=pow_mod(3,mod-2,mod)*p%mod;
        q=pow_mod(2,(temp-1+mod-1)%(mod-1),mod);
        if(!flag)q=3*q%mod;
        cout<<p<<"/"<<q<<endl;
        return 0;
}