Intersection between 2d conic in OpenCASCADE

Intersection between 2d conic in OpenCASCADE

eryar@163.com

Abstract. OpenCASCADE provides the algorithm to implement of the intersection between two 2d conic curve. The conic is defined by its implicit quadaratic equation, so the intersection problem is become a polynomial roots finding problem. The paper focus on the two conic curve intersection algorithm implementation.

Key Words. 2d conic intersection, conic equation,

1.Introduction

高中的时候学习了直线Line、圆Circle、圆锥曲线Conic（椭圆Ellipse、双曲线Hyperbola和抛物线parabola）等二维曲线的方程及特性，也可以对他们之间的相交情况进行计算。如何编程实现任意两个圆锥曲线相交呢？本文通过对OpenCASCADE中二维圆锥曲线相交代码的分析来理解其实现原理。

Figure 1. 圆锥曲线相交

2.Conic Implicit Equation

圆锥曲线一般的代数表示方法为：

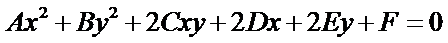
OpenCASCADE中使用类IntAna2d_Conic来表示圆锥曲线的代数方程。并提供了将二维曲线（直线、圆、椭圆、抛物线、双曲线）转换成代数方程的方法，相关代码如下所示：

IntAna2d_Conic::IntAna2d_Conic (const gp_Lin2d& L) {

  a = 0.0;
  b = 0.0;
  c = 0.0;
  L.Coefficients(d,e,f);
  f = *f;
}

IntAna2d_Conic::IntAna2d_Conic (const gp_Circ2d& C) {

  C.Coefficients(a,b,c,d,e,f);
}

IntAna2d_Conic::IntAna2d_Conic (const gp_Elips2d& E) {

  E.Coefficients(a,b,c,d,e,f);
}

IntAna2d_Conic::IntAna2d_Conic (const gp_Parab2d& P) {
  P.Coefficients(a,b,c,d,e,f);
}

IntAna2d_Conic::IntAna2d_Conic (const gp_Hypr2d& H) {
  H.Coefficients(a,b,c,d,e,f);
}
 

3.Intersection between Circle and Conic

当对二维圆和圆锥曲线进行求交时，先得到圆的半径和圆锥曲线的一般式方程。将圆用参数方程表示并代入圆锥曲线的一般式方程中得到：

所以圆和圆锥曲线求交问题转换为三角函数方程求解的问题。OpenCASCADE的math包中提供了类math_TrigonometricFunctionRoots来求解如下三角函数方程的根：

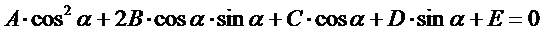
直接将对应的系数传入即可对如上形式的三角函数方程进行求根。OpenCASCADE中圆和圆锥曲线求交的代码如下所示：

void IntAna2d_AnaIntersection::Perform(const gp_Circ2d& Circle,
  const IntAna2d_Conic& Conic)
{
   Standard_Boolean CIsDirect = Circle.IsDirect();
   Standard_Real A,B,C,D,E,F;
   Standard_Real pcc,pss,p2sc,pc,ps,pcte;
   Standard_Real radius=Circle.Radius();
   Standard_Real radius_P2=radius*radius;
   Standard_Integer i;
   Standard_Real tx,ty,S;

   done = Standard_False;
   nbp  = ;
   para = Standard_False;
   empt = Standard_False;
   iden = Standard_False;

   gp_Ax2d Axe_rep(Circle.XAxis());

   Conic.Coefficients(A,B,C,D,E,F);
   Conic.NewCoefficients(A,B,C,D,E,F,Axe_rep);

   // Parametre a avec x=Radius Cos(a)  et y=Radius Sin(a)

   pss = B*radius_P2;
   pcc = A*radius_P2 - pss;                            // COS ^2
   p2sc =C*radius_P2;                                  // 2 SIN COS
   pc  = 2.0*D*radius;                                 // COS
   ps  = 2.0*E*radius;                                 // SIN
   pcte= F + pss;                                      //

   math_TrigonometricFunctionRoots Sol(pcc,p2sc,pc,ps,pcte,0.0,2.0*M_PI);

   if(!Sol.IsDone()) {
     cout << "\n\nmath_TrigonometricFunctionRoots -> NotDone\n\n"<<endl;
     done=Standard_False;
     return;
   }
   else {
     if(Sol.InfiniteRoots()) {
       iden=Standard_True;
       done=Standard_True;
       return;
     }
     nbp=Sol.NbSolutions();
     for(i=;i<=nbp;i++) {
       S = Sol.Value(i);
       tx= radius*Cos(S);
       ty= radius*Sin(S);
       Coord_Ancien_Repere(tx,ty,Axe_rep);
       if(!CIsDirect)
S = M_PI+M_PI-S;
       lpnt[i-].SetValue(tx,ty,S);
     }
     Traitement_Points_Confondus(nbp,lpnt);
   }
   done=Standard_True;
 }

上述代码的实现过程如下：先计算出圆锥曲线在圆的坐标系下的一般式方程的系数，再用圆的参数方程代入圆锥曲线的一般式将二元二次方程转换成一元三角函数方程，最后对三角函数方程进行求解。

 
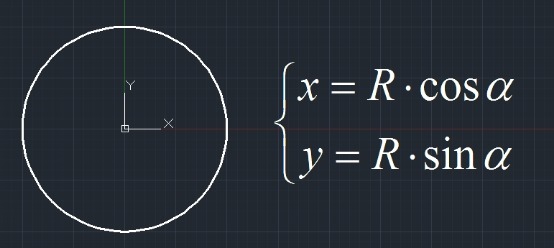
Figure 2. 圆及其参数方程

4.Intersection between Ellipse and Conic

二维椭圆与圆锥曲线求交的实现与圆的实现类似，唯一不同的就是椭圆的参数方程与圆的参数稍有不同。

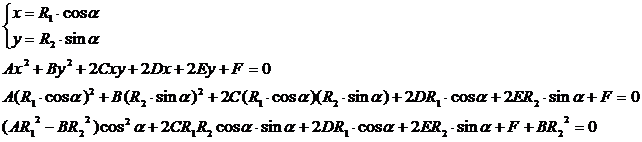
依然使用椭圆的参数方程将圆锥曲线的二元二次方程化为一元的三角函数方程，再对三角函数方程进行求解。相关代码如下所示：

void IntAna2d_AnaIntersection::Perform(const gp_Elips2d& Elips,
  const IntAna2d_Conic& Conic)
{
  Standard_Boolean EIsDirect = Elips.IsDirect();
  Standard_Real A,B,C,D,E,F;
  Standard_Real pcte,ps,pc,p2sc,pcc,pss;
  Standard_Real minor_radius=Elips.MinorRadius();
  Standard_Real major_radius=Elips.MajorRadius();
  Standard_Integer i;
  Standard_Real tx,ty,S;

  done = Standard_False;
  nbp = ;
  para = Standard_False;
  iden = Standard_False;
  empt = Standard_False;

  gp_Ax2d Axe_rep(Elips.XAxis());

  Conic.Coefficients(A,B,C,D,E,F);
  Conic.NewCoefficients(A,B,C,D,E,F,Axe_rep);  

  // Parametre : a avec x=MajorRadius Cos(a)  et y=MinorRadius Sin(a)

  pss= B*minor_radius*minor_radius;                   // SIN ^2
  pcc= A*major_radius*major_radius-pss;               // COS ^2
  p2sc=C*major_radius*minor_radius;                   // 2 SIN COS
  pc= 2.0*D*major_radius;                             // COS
  ps= 2.0*E*minor_radius;                             // SIN
  pcte=F+pss;                                         //

  math_TrigonometricFunctionRoots Sol(pcc,p2sc,pc,ps,pcte,0.0,2.0*M_PI);

  if (!Sol.IsDone()) {
    done=Standard_False;
    return;
  }
  else {
    if(Sol.InfiniteRoots()) {
      iden=Standard_True;
      done=Standard_True;
      return;
    }
    nbp=Sol.NbSolutions();
    for(i=;i<=nbp;i++) {
      S = Sol.Value(i);
      tx=major_radius*Cos(S);
      ty=minor_radius*Sin(S);
      Coord_Ancien_Repere(tx,ty,Axe_rep);
      if(!EIsDirect)
S = M_PI+M_PI-S;
      lpnt[i-].SetValue(tx,ty,S);
    }
    Traitement_Points_Confondus(nbp,lpnt);
  }
  done = Standard_True;
}
 

 

 

5.Intersection between Parabola and Conic

将抛物线Parabola的标准方程代入圆锥曲线的一般式方程可将二元二次方程化成一元四次方程：

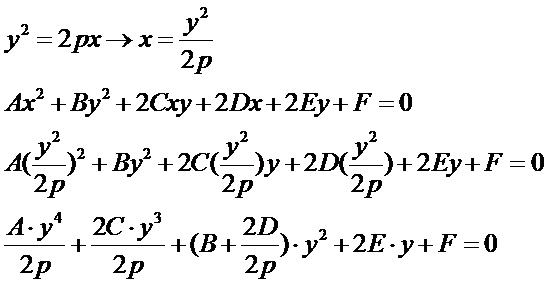
再对这个一元四次方程进行求解，相关代码如下所示：

void IntAna2d_AnaIntersection::Perform(const gp_Parab2d& P,
       const IntAna2d_Conic& Conic)
  {
    Standard_Boolean PIsDirect = P.IsDirect();
    Standard_Real A,B,C,D,E,F;
    Standard_Real px4,px3,px2,px1,px0;
    Standard_Integer i;
    Standard_Real tx,ty,S;
    Standard_Real un_sur_2p=0.5/(P.Parameter());
    gp_Ax2d Axe_rep(P.MirrorAxis());

    done = Standard_False;
    nbp = ;
    para = Standard_False;
    empt = Standard_False;
    iden = Standard_False; 

    Conic.Coefficients(A,B,C,D,E,F);
    Conic.NewCoefficients(A,B,C,D,E,F,Axe_rep); 

    //-------- 'Parametre'  y avec y=y  x=y^2/(2 p)

    px0=F;
    px1=E+E;
    px2=B + un_sur_2p*(D+D);
    px3=(C+C)*un_sur_2p;
    px4=A*(un_sur_2p*un_sur_2p);

    MyDirectPolynomialRoots Sol(px4,px3,px2,px1,px0);

    if(!Sol.IsDone()) {
      done=Standard_False;
    }
    else {
      if(Sol.InfiniteRoots()) {
iden=Standard_True;
done=Standard_True;
      }
      nbp=Sol.NbSolutions();
      for(i=;i<=nbp;i++) {
S = Sol.Value(i);
tx=un_sur_2p*S*S;
ty=S;
Coord_Ancien_Repere(tx,ty,Axe_rep);
if(!PIsDirect)
  S =-S;
lpnt[i-].SetValue(tx,ty,S);
      }
      Traitement_Points_Confondus(nbp,lpnt);
    }
    done=Standard_True;
  }
 

 

6.Conclusion

圆（椭圆）与圆锥曲线相交，将圆（椭圆）的参数方程代入圆锥曲线的一般式，将圆锥曲线方程化为三角函数方程，再对三角函数方程进行求解得到交点。

抛物线与圆锥曲线相交，将抛物线方程代入圆锥曲线的一般式，将圆锥曲线方程化为一元四次方程，再对方程进行求解得到交点。

综上所述，二维圆锥曲线相交的处理都是利用圆锥曲线的一般式与相应的参数方程化为一元函数方程，再对方程进行求解。

7.References

1. 人民教育出版社中学数学室. 数学第二册上. 人民教育出版社. 2000

2. 同济大学数学教研室. 高等数学. 高等教育出版社. 1996

3. 易大义, 沈云宝, 李有法. 计算方法. 浙江大学出版社. 2002

4. 李原, 张开富, 余剑峰. 计算机辅助几何设计技术及应用. 西北工业大学出版社. 2007

5. 丘维声. 解析几何. 北京大学出版社. 1996

PDF Version: Intersection between 2d conic in OpenCASCADE