Codeforces 601B. Lipshitz Sequence（单调栈）

Codeforces 601B. Lipshitz Sequence



题意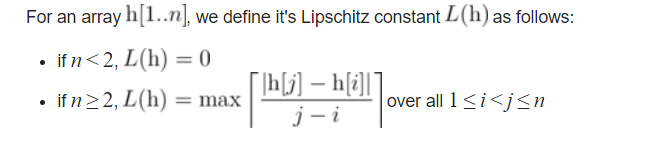：，q个询问，每次询问给出l,r，求a数组[l,r]中所有子区间的L值的和。

思路：首先要观察到，斜率最大值只会出现在相邻两点上，因此可以处理出d数组，d[i]=a[i]-a[i-1]。则问题转化为求d数组在指定区间内，所有子区间的最大值的和。枚举子区间的复杂度是平方级别，显然是不能接受的，所以可以用单调栈预处理出每个d[i]可以成为最大值的最大区间（形象地说，也就是d[i]为最大值的域可以延伸到左、右各多远），用l，r数组保存这个信息，这样面对每次询问，只需要O(n)遍历d数组指定区间，累加d[i]*“d[i]为最值的区间个数”（这个可以根据l[i]，r[i]的信息O（1）算出），累加结果即为本次询问答案。总的复杂度为O(q*n)。

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<vector>
#include<map>
#include<set>
#include<queue>
#include<cstring>
#include<cmath>
#include<functional>
#include<climits>
#include<string>
#define dd(x) cout<<#x<<" = "<<x<<" "
#define de(x) cout<<#x<<" = "<<x<<"\n"
#define Clear(x,y) memset(x,y,sizeof(x))
#define pb push_back
#define mp make_pair
#define fi first
#define se second
#define lson l,m,rt<<1
#define rson m+1,r,rt<<1|1
using namespace std;
typedef long long ll;
typedef long double ld;
typedef pair<int,int> P;
typedef vector<int> V;
typedef map<int,int> M;
typedef set<int> S;
typedef queue<int> Q;
typedef priority_queue<int> BQ;
typedef priority_queue<int,vector<int>,greater<int> > SQ;
const int maxn=1e5+10,mod=1e9+7,INF=0x3f3f3f3f;
int a[maxn],d[maxn],l[maxn],r[maxn],stack[maxn],top;
void init(int n)
{
	for (int i=2;i<=n;++i)
	{
		while (top>0&&d[stack[top]]<=d[i])
			r[stack[top--]]=i-1;
		l[i]=stack[top]+1;
		stack[++top]=i;
	}
	while (top>0)
		r[stack[top--]]=n;
}
int main()
{
	int n,q;
	scanf("%d%d",&n,&q);
	for (int i=1;i<=n;++i)
	{
		scanf("%d",&a[i]);
		d[i]=abs(a[i]-a[i-1]);
	}
	init(n);
	while (q--)
	{
		int L,R;
		scanf("%d%d",&L,&R);
		ll ans=0;
		for (int i=L+1;i<=R;++i)
		{
			int _l=max(l[i]-1,L),_r=min(r[i],R);
			ans+=ll(d[i])*(i-_l)*(_r-i+1);
		}
		printf("%lld\n",ans);
	}
	return 0;
}