P1115 最大子段和&P1719 最大加权矩形

上接：DP&图论 DAY 1 上午

这两个题本质是一个亚子，所以放一起啦

DPDPDPDPDPDPDPDP

P1115 最大子段和

题解

因为题目要求的是一段连续的区间，所以前缀和搞暴力？？？

我们设置数组 f[ i ] 表示以 a[ i ] 结尾的最大连续子段和

那么转移？？？

1.接着上一段，继续构成一段连续的子段 continue the old life

2.自成一段  和过去 say goodbye

转移方程：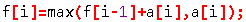 

ans记录最大值就好啦

代码

#include<bits/stdc++.h>

using namespace std;

inline int read()
{
    int ans=;
    char last=' ',ch=getchar();
    while(ch<''||ch>'') last=ch,ch=getchar();
    while(ch>=''&&ch<='') ans=ans*+ch-'',ch=getchar();
    if(last=='-') ans=-ans;
    return ans;
}

const int maxn=2e5+;
int n,ans;
int a[maxn];
int f[maxn];

int main()
{
    n=read();
    for(int i=;i<=n;i++)
      a[i]=read();
    f[]=;f[]=a[];
    ans=a[];
    for(int i=;i<=n;i++)
    {
        f[i]=max(f[i-]+a[i],a[i]);
        ans=max(ans,f[i]);
    }
    printf("%d\n",ans);

    return ;
}

P1719 最大加权矩形

题解

其实这个题就是上一个的变式，我们只需要把本题的二维转变成一维就好啦！

考虑枚举子矩阵的上下界

确定了上下界，就缩成了一维，此时只需要算 “该行” ，的最大 f[ ] 就好啦！

解释一下数组：

a[ i ][ j ] ：读入给出的矩阵

sum[ i ][ j ] ：第 j 列，前 i 行的前缀和

其实这里的 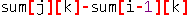就相当于上一个题的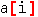

代码

#include<iostream>
#include<cstdlib>
#include<cstdio>
#include<string>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<queue>

using namespace std;

inline int read()
{
    int ans=;
    char last=' ',ch=getchar();
    while(ch<''||ch>'') last=ch,ch=getchar();
    while(ch>=''&&ch<='') ans=ans*+ch-'',ch=getchar();
    if(last=='-') ans=-ans;
    return ans;
}

const int maxn=;
int n,ans=-;
int a[maxn][maxn],sum[maxn][maxn],f[maxn];

int main()
{
    n=read();
    for(int i=;i<=n;i++)
       for(int j=;j<=n;j++)
           a[i][j]=read(),sum[i][j]=sum[i-][j]+a[i][j];

    for(int i=;i<=n;i++)
      for(int j=i;j<=n;j++)   //枚举上下界 i~j
      {
          memset(f,,sizeof(f));
          for(int k=;k<=n;k++)   //DP
            f[k]=max(f[k-]+(sum[j][k]-sum[i-][k]),(sum[j][k]-sum[i-][k])),
            ans=max(ans,f[k]);
      }

    printf("%d",ans);
    return ;
}