2018 南京预选赛 J Sum ( 欧拉素数筛 、Square-free Number、DP )

题目链接

题意 :

定义不能被平方数整除的数为 Square-free Number

定义 F(i) = 有几对不同的 a 和 b 使得 i = a * b 且 a 、b 都是 Square-free

给出一个 N 求

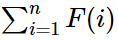
分析 :

首先 Square-free 有一个性质

就是用唯一分解定理将 Square-free Number 分解后

素因数的指数都是 1

那么对于 a、b 是 Square-free Number

相乘 a * b 得出的 i 其不会有素因子的指数超过 2

然后你要熟悉欧拉筛

欧拉筛之所以是线性是因为、它保证筛出来的合数

都是用其最小质因子筛出来的、且做到不重复

定义 dp[i] = 题目所述的 F[i]  初始化  dp[1] = 1

然后在欧拉筛中进行动态规划、分几种情况

if  i  is prime number dp[i] = 2 ( 分别可以是 a 可以是 b )

if  ( i % prime[j] != 0 ) dp[i] = dp[i] * dp[prime[j]] ( i 不是 prime[j] 的倍数、此方程显然 )

if  ( i % prime[j] == 0){ (表示 i 至少包含了一个 prime[j] )

　　if( i % (prime[j]^2) == 0 ) dp[i*prime[j]] = 0 ( i * prime[j] 肯定有素因数指数 > 2 )

　　else if( i % prime[j] == 0 )  dp[i*prime[j]] = dp[i/prime[j]] ( i * prime[j] 会使得 prime[j] 这个因子指数为 2、所以就少了它的数量 )

}

#include<bits/stdc++.h>
#define LL long long
#define ULL unsigned long long
 
#define scl(i) scanf("%lld", &i)
#define scll(i, j) scanf("%lld %lld", &i, &j)
#define sclll(i, j, k) scanf("%lld %lld %lld", &i, &j, &k)
#define scllll(i, j, k, l) scanf("%lld %lld %lld %lld", &i, &j, &k, &l)
 
#define scs(i) scanf("%s", i)
#define sci(i) scanf("%d", &i)
#define scd(i) scanf("%lf", &i)
#define scIl(i) scanf("%I64d", &i)
#define scii(i, j) scanf("%d %d", &i, &j)
#define scdd(i, j) scanf("%lf %lf", &i, &j)
#define scIll(i, j) scanf("%I64d %I64d", &i, &j)
#define sciii(i, j, k) scanf("%d %d %d", &i, &j, &k)
#define scddd(i, j, k) scanf("%lf %lf %lf", &i, &j, &k)
#define scIlll(i, j, k) scanf("%I64d %I64d %I64d", &i, &j, &k)
#define sciiii(i, j, k, l) scanf("%d %d %d %d", &i, &j, &k, &l)
#define scdddd(i, j, k, l) scanf("%lf %lf %lf %lf", &i, &j, &k, &l)
#define scIllll(i, j, k, l) scanf("%I64d %I64d %I64d %I64d", &i, &j, &k, &l)
 
#define lson l, m, rt<<1
#define rson m+1, r, rt<<1|1
#define lowbit(i) (i & (-i))
#define mem(i, j) memset(i, j, sizeof(i))
 
#define fir first
#define sec second
#define VI vector<int>
#define ins(i) insert(i)
#define pb(i) push_back(i)
#define pii pair<int, int>
#define VL vector<long long>
#define mk(i, j) make_pair(i, j)
#define all(i) i.begin(), i.end()
#define pll pair<long long, long long>
 
#define _TIME 0
#define _INPUT 0
#define _OUTPUT 0
clock_t START, END;
void __stTIME();
void __enTIME();
void __IOPUT();
using namespace std;
 
;
 
bool isPrime[maxn];
LL Prime[maxn]; ;
LL dp[maxn];
LL ans[maxn];
 
inline void init()
{
    dp[] = ;
    ans[] = 1LL;
 
    mem(isPrime, true);
 
    ; i<=(maxn-); i++){
 
        if(isPrime[i]){
            dp[i] = ;
            Prime[tot++] = i;
        }
 
        ; j<tot && i*Prime[j]<=(maxn-); j++){
 
            isPrime[i*Prime[j]] = false;
 
            ){
 
                ) dp[i*Prime[j]] = ;
                else dp[i*Prime[j]] = dp[i / Prime[j]];
 
                break;
 
            }else dp[i*Prime[j]] = dp[i] * dp[Prime[j]];
        }
        ans[i] = ans[i-] + (LL)dp[i];
    }
}
 
int main(void){__stTIME();__IOPUT();
 
    init();
 
    int nCase;
    sci(nCase);
 
    while(nCase--){
        int n;
        sci(n);
        printf("%lld\n", ans[n]);
    }
 
__enTIME();;}
 
void __stTIME()
{
    #if _TIME
        START = clock();
    #endif
}
 
void __enTIME()
{
    #if _TIME
        END = clock();
        cerr<<"execute time = "<<(double)(END-START)/CLOCKS_PER_SEC<<endl;
    #endif
}
 
void __IOPUT()
{
    #if _INPUT
        freopen("in.txt", "r", stdin);
    #endif
    #if _OUTPUT
        freopen("out.txt", "w", stdout);
    #endif
}