R语言与概率统计(六) 主成分分析 因子分析

超高维度分析，N*P的矩阵，N为样本个数，P为指标，N<<P

PCA:抓住对y对重要的影响因素

主要有三种：PCA,因子分析，回归方程+惩罚函数（如LASSO）

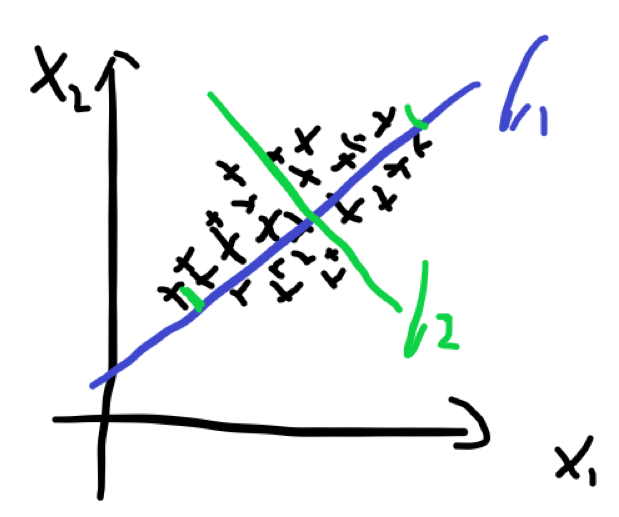
为了降维，用更少的变量解决问题，如果是二维的，那么就是找到一条线，要使这些点再线上的投影最大，投影最大，就是越分散，就考虑方差最大。

> conomy<-data.frame(
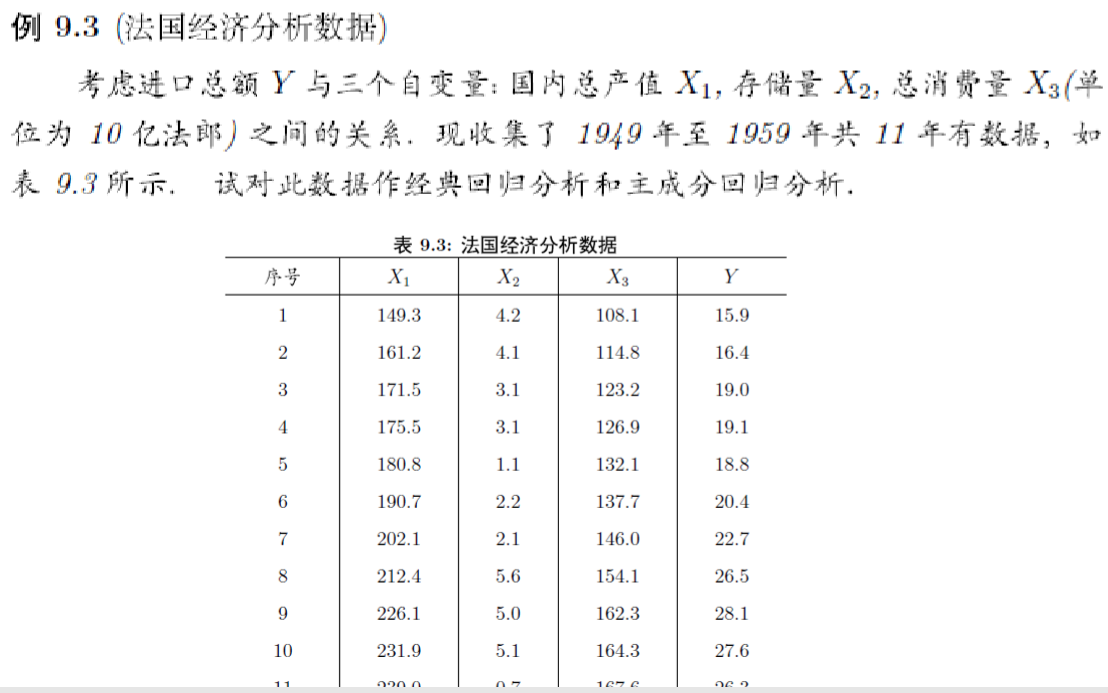
+   x1=c(149.3, 161.2, 171.5, 175.5, 180.8, 190.7,
+        202.1, 212.4, 226.1, 231.9, 239.0),
+   x2=c(4.2, 4.1, 3.1, 3.1, 1.1, 2.2, 2.1, 5.6, 5.0, 5.1, 0.7),
+   x3=c(108.1, 114.8, 123.2, 126.9, 132.1, 137.7,
+        146.0, 154.1, 162.3, 164.3, 167.6),
+   y=c(15.9, 16.4, 19.0, 19.1, 18.8, 20.4, 22.7,
+       26.5, 28.1, 27.6, 26.3)
+ )
> #### 作线性回归
> lm.sol<-lm(y~x1+x2+x3, data=conomy)
> summary(lm.sol)

Call:
lm(formula = y ~ x1 + x2 + x3, data = conomy)

Residuals:
     Min       1Q   Median       3Q      Max
-0.52367 -0.38953  0.05424  0.22644  0.78313 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)
(Intercept) -10.12799    1.21216  -8.355  6.9e-05 ***
x1           -0.05140    0.07028  -0.731 0.488344
x2            0.58695    0.09462   6.203 0.000444 ***
x3            0.28685    0.10221   2.807 0.026277 *
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.4889 on 7 degrees of freedom
Multiple R-squared:  0.9919,	Adjusted R-squared:  0.9884
F-statistic: 285.6 on 3 and 7 DF,  p-value: 1.112e-07

> #### 作主成分分析
> conomy.pr<-princomp(~x1+x2+x3, data=conomy, cor=T)
> summary(conomy.pr, loadings=TRUE)
Importance of components:
                         Comp.1    Comp.2       Comp.3
Standard deviation     1.413915 0.9990767 0.0518737839
Proportion of Variance 0.666385 0.3327181 0.0008969632
Cumulative Proportion  0.666385 0.9991030 1.0000000000

Loadings:
   Comp.1 Comp.2 Comp.3
x1  0.706         0.707
x2        -0.999
x3  0.707        -0.707
> #### 预测测样本主成分, 并作主成分分析
> pre<-predict(conomy.pr)
> conomy$z1<-pre[,1]
> conomy$z2<-pre[,2]
> lm.sol<-lm(y~z1+z2, data=conomy)
> summary(lm.sol)

Call:
lm(formula = y ~ z1 + z2, data = conomy)

Residuals:
     Min       1Q   Median       3Q      Max
-0.89838 -0.26050  0.08435  0.35677  0.66863 

Coefficients:
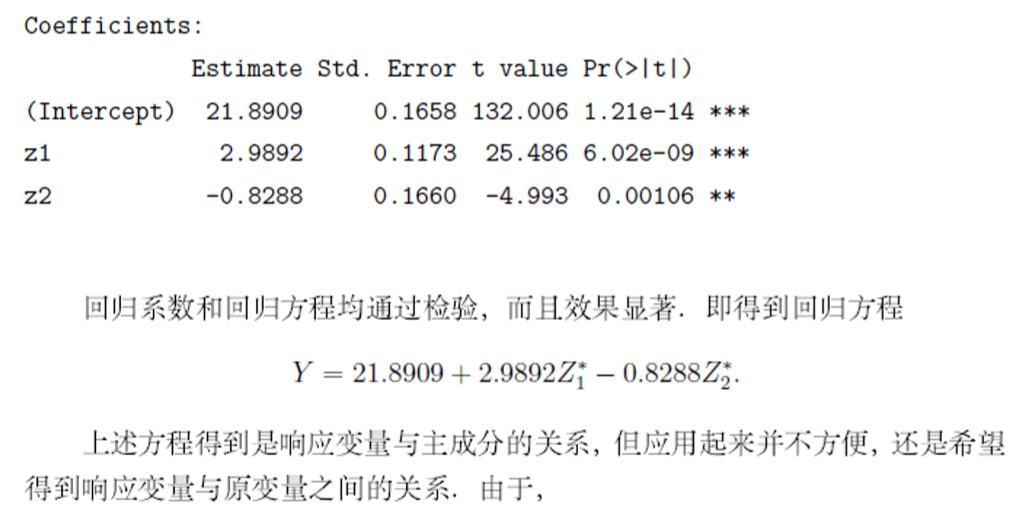
            Estimate Std. Error t value Pr(>|t|)
(Intercept)  21.8909     0.1658 132.006 1.21e-14 ***
z1            2.9892     0.1173  25.486 6.02e-09 ***
z2           -0.8288     0.1660  -4.993  0.00106 **
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.55 on 8 degrees of freedom
Multiple R-squared:  0.9883,	Adjusted R-squared:  0.9853
F-statistic: 337.2 on 2 and 8 DF,  p-value: 1.888e-08

> #### 作变换, 得到原坐标下的关系表达式
> beta<-coef(lm.sol); A<-loadings(conomy.pr)
> x.bar<-conomy.pr$center; x.sd<-conomy.pr$scale
> coef<-(beta[2]*A[,1]+ beta[3]*A[,2])/x.sd
> beta0 <- beta[1]- sum(x.bar * coef)
> c(beta0, coef)
(Intercept)          x1          x2          x3
-9.13010782  0.07277981  0.60922012  0.10625939