MLN 讨论 —— 基础知识

一. MLN相关知识的介绍

1. First-order logic

• A first-order logic knowledge base (KB) is a set of formulas in first-order logic;
• Predicate symbols represent relations among objects in the domain (e.g., Friends) or attributes of objects (e.g., Smokes)
• An atomic formula is a predicate symbol applied to a tuple of terms.
• Formulas are recursively constructed from atomic formulas using logical connectives and quantifiers.
• A term can be a constant, variable, or a function;
• A ground term is a term containing no variables;
• A ground atom or ground predicate is an atomic formula all of whose arguments are ground terms.
• A possible world assigns a truth value to each possible ground predicate.

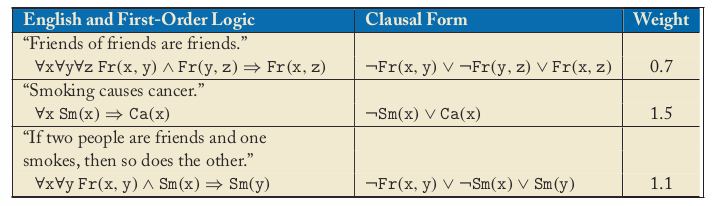
对于某个自然语言的语句： 例如 "Friends of friends are friends."  我们可以先把他转换为Formula "∀x∀y∀z Fr(x,y) ∧ Fr(y,z) ⇒ Fr(x,z)", 然后把Formula转换为conjunctive normal form (CNF)；这样，对于每一个possible world , 我们就可以轻易的知道Formula的Truth Value了；

A first-order KB can be seen as a set of hard constraints on the set of possible worlds: if a world violates even one formula, it has zero probability. The basic idea in MLNs is to soften these constraints: When a world violates one formula in the KB it is less probable, but not impossible. The fewer formulas a world violates, the more probable it is. Each formula has an associated weight that reflects how strong a constraint it is.

2. Markov Networks

这里需要注意几点：

1. Markov network is composed of an undirected graph G and a set of potential function.

2. The graph has a node for each variable, and the model has a potential function for each clique in the graph.

3. Mark Logic

(1) 图的结构

contains one binary node for each possible grounding of each predicate appearing in L.

There is an edge between two nodes iff the corresponding ground predicates appear together in at least one grounding of one formula in L.

（2）构造MLN的例子

Formulas:  ∀x Smoke(x) ⇒ Cancer(x)   ,   ∀x∀y Friends(x,y) ∧ Smoke(x) ⇒ Smoke(y)

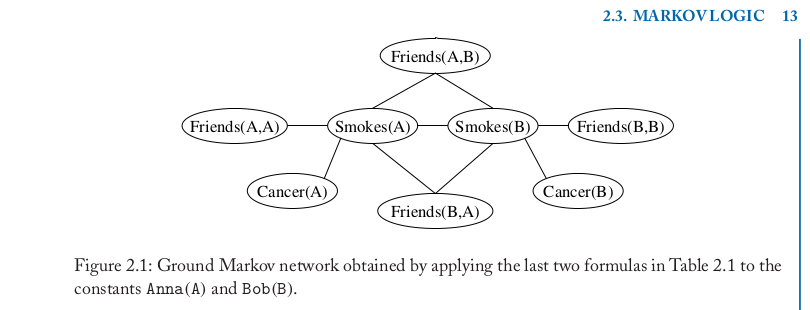
M(L,C) can now be used to infer the probability that Anna and Bob are friends given their smoking habits, the probability that Bob has cancer given his friendship with Anna and whether she has cancer, etc.

（3）计算公式

(4) 简化MLNs使用的假设

有了这些假设，就能够从first-order formula中产生a set of ground formulas，从而应用上面的计算公式；

简化过程的伪代码如下：

The last assumption allows us to replace functions by their values when grounding formulas. Thus the only ground predicates that need to be considered are those having constants as argument. The infinite number of terms constructible from all functions and constants in (L, C) can be ignored, because each of those terms corresponds to a known constant in C, and predicates involving them are already represented as the predicates involving the corresponding constants. The possible groundings of a predicate are thus obtained simply by replacing each variable in the predicate with each constant in C, and replacing each function term in the predicate by the corresponding constant.

(4) 怎么表示这3个假设？

(5) 计算概率的一个小例子

（6）如何计算w ?

二. ProbCog

1. 历史渊源 

Alchemy is a Statistical relational AI , recommended by Professor Pedro Domingos ; PyMLNs is a GUI with plug-in capabilities for Alchemy; PyMLNs has been merged into ProbCog;

Alchemy 目前还没有实验成功，可能为依赖库和操作系统的问题 (Fedora Core 7, Bison 2.3, Flex 2.5.4, g++ 4.1.2, Perl 5.8.8)

ProbCog的相关介绍可以点击这里[github]

2. 使用介绍

ProbCog关于MLN部分的使用步骤[github]为：  mlnlearn, mlnquery(infer)

(1) mlnlearn

待训练的MLN: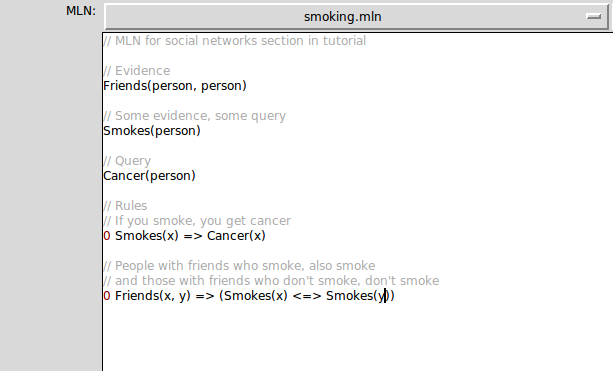 

包含一些predicates和formulas，注意formulas前面的参数为0，表示还未训练

待训练的db：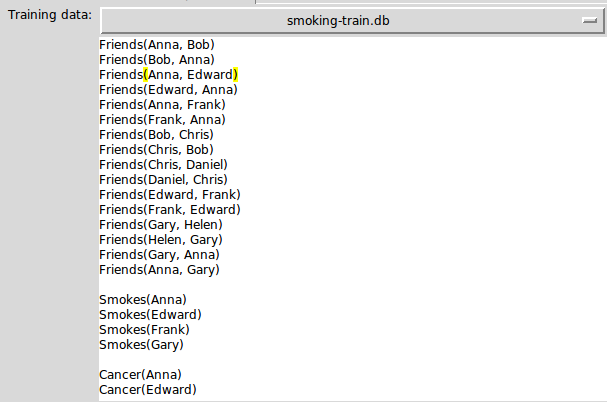　

训练出来的结果：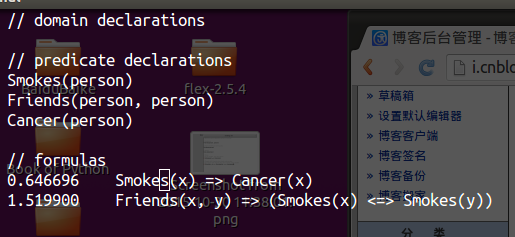　

（2）mlnquery

查询界面：

查询结果：

3. 待研究

(1) mlnlearn参数训练结果的解释

(2) mlnquery查询结果的解释

(3) 使用python脚本操作