10月清北学堂培训 Day 5

今天是廖俊豪老师的讲授~

T1

第一次想出正解

30 pts：

k <= 10，枚举如何把数放到矩阵中，O ( k ! )；

100 pts：

对于矩阵的每一列，我们二分最小差异值，然后贪心去判断是否可行；

贪心策略：从前往后找，如果有从某个数开始往后连续的 m 个数，这 m 个数的最大值 - 最小值 < k，那么就把这 m 个数放到同一行，最后判断是否能够凑出 n 行；

std 标程：

#include<bits/stdc++.h>
using namespace std;

const int maxn = 1e5 + ;
int n, m, k, v[maxn];

int judge(int d)
{
    int tmp = ;
    for (int i=; i+m-<=k; ++i)
    {
        if (v[i+m-] - v[i] <=d)
            ++tmp, i += m - ;
    }
    if (tmp >= n) return ;
    return ;
}

int main()
{
    freopen("a.in", "r", stdin);
    freopen("a.out", "w", stdout);
    scanf("%d%d%d", &k, &n, &m);
    for (int i=; i<=k; ++i)
        scanf("%d", &v[i]);
    sort(v + , v + k + );
    int left = , right = 1e9;
    while (left < right)
    {
        int mid = (left + right) / ;
        if (judge(mid))
            right = mid;
        else
            left = mid + ;
    }
    printf("%d\n", left);
    return ;
}

我的拙码：

#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
using namespace std;
int read()
{
    char ch=getchar();
    int a=,x=;
    while(ch<''||ch>'')
    {
        if(ch=='-') x=-x;
        ch=getchar();
    }
    while(ch>=''&&ch<='')
    {
        a=(a<<)+(a<<)+(ch-'');
        ch=getchar();
    }
    return a*x;
}
const int N=5e5;
int n,k,m,l,r=-1e9,ans;
int val[N];
bool check(int x)             //每行最大值减去最小值都要小于等于x
{
    int tot=;                //我们能匹配到tot行了
    for(int i=;i+m-<=k;i++)
    {
        if(val[i+m-]-val[i]<=x) //中间的点都可以选在同一行,那么两头的分别就是最大最小值
        {
            tot++;
            i=i+m-;
        }
        if(tot==n) return ;
    }
    if(tot<n) return ;
    else return ;
}
int main()
{
    freopen("a.in","r",stdin);
    freopen("a.out","w",stdout);
    k=read();n=read();m=read();
    for(int i=;i<=k;i++)
    {
        val[i]=read();
        r=max(r,val[i]);
    }
    sort(val+,val++k);
    l=;
    while(l<r)
    {
        int mid=(l+r)>>;
        if(check(mid)) r=mid,ans=mid;
        else l=mid+;
    }
    printf("%d",ans);
    return ;
}

T2

30 pts：

枚举分割点的位置，然后一顿瞎搞，O ( n ! ) ；

60 pts：

我们完全可以用 dp 来做（然后我就写炸了。。。）

我们先预处理出每一段的或和， 用 sum [ i ][ j ] 存起来；

f [ i ][ j ] 表示考虑了前 i 个数，分成 j 段的最大和 。

考虑转移：

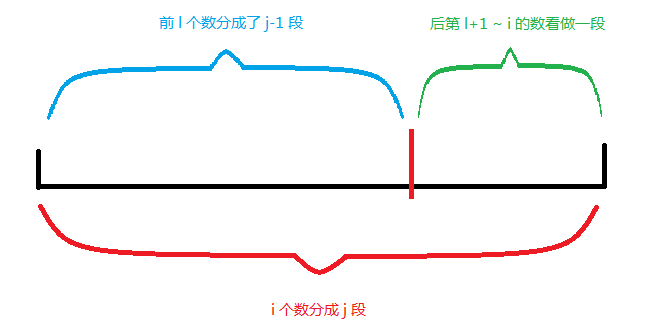
f [ i ][ j ] = max ( f [ i ][ j ] , f [ l ][ j-1 ] + sum [ l+1 ][ i ]；

100 pts：

我们考虑去优化 dp；

我们发现两个数组具有单调性：

f [ l ][ j-1 ] 随着 l 的增加递增；

sum [ l+1 ][ i ] 随着 l 的增加而递减；

对于固定的 i，sum [ k+1 ][ j ] 的取值最多只有 32 种，而且 f 数组的值单调递增。预处理出转移点即可。

时间复杂度 O ( n * k * log C )，C 为 v [ i ] 的上界

100+ pts：

时间复杂度 O ( n k ) ? O ( n log C ) ? 欢迎补充

B_extended：将最大值改为最小值，怎么做？

T3

令 n = 2^k , C ( x , y ) 为在 x 个物品中选择 y 个不同的物品的方案数，树的最底层为 0 。

30 pts：

k <= 3，也就是说 n <=8 ，我们可以直接枚举 n 的全排列，把所有的情况加起来！

60 pts：

k <= 10，n <= 1024；

求出所有情况的魔法值；

考虑：两个点 x 和点 y 在第 d 层对答案的贡献；

算清楚 x 和 y 在第 d 层相遇了多少次：Σ（v [ x ] * v [ y ] * times [ x ][ y ][ d ]）；

不妨考虑 2^d - 1 个编号小于 y 的；

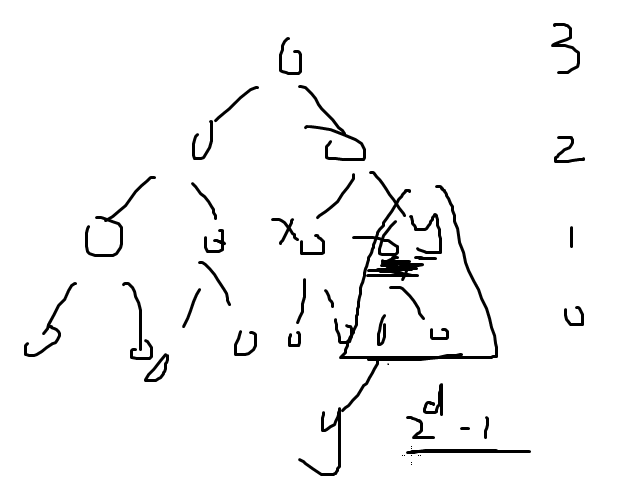
这才 60 pts 就已经晕了，那么接下来讲 100pts 的：

更改求和顺序，改为 2 * 2^k! * 2^k! * ( n - 2^k+1 ) ! * C ( y-1 , 2^k - 1 ) * v [ y ] * C ( x - 1 - 2^k ,  2^k-1) * v [ x ] ，枚举 k 和 y，我们知道 x >= max ( 2^k+1 ,  y+1 )，先对 C ( x - 1 - 2^k ,  2^k - 1 ) * v [ x ] 求后缀和即可。时间复杂度 O ( n * k )；

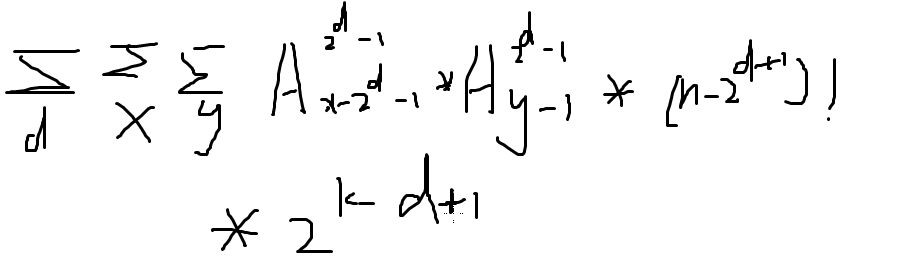
我们可以预处理：

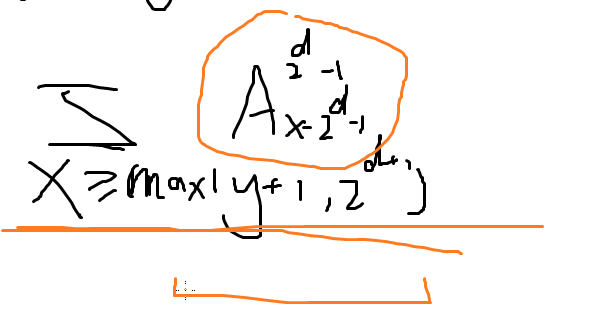
数论

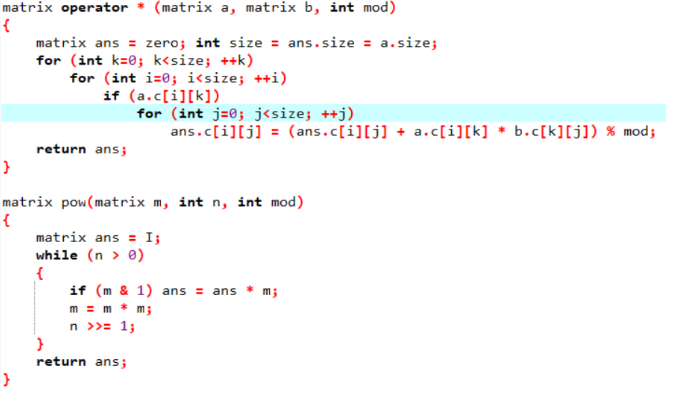
POJ 3735  Training little cats

有 n 只猫，有三种操作：

1、让第 i 只猫花生数 +1；
2、吃光第 i 只猫拥有的花生；
3、交换两只猫拥有的花生；
给出一个长度为 k 的操作序列，求将这个操作序列循环 m 次之后，每只猫拥有的花生数量；

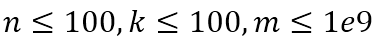
题解：

在线性代数中，矩阵乘法可以表示向量的变换；

将 n 只猫拥有的花生数量看成一个列向量；

操作1：向量的平移变换；

操作2：向量的投影变换；

操作3：向量的旋转变换；

找出每种操作对应的矩阵，依次做乘法即可；

考虑到 n 的范围太大， O ( n ) 的算法不大行，我们要想 log n 的算法；

自然想到了快速幂，我们用矩阵快速幂试试：

考虑到 k 是在不断变化的，但是最多就 18 种，所以我们做 18 次矩阵快速幂就好了，总时间复杂度 O（18 * 3³ * log n）；

欧几里得算法：

给定数 a 和数 b，求两个数的最大公约数；

欧几里得算法（辗转相除法）

gcd（a , b）= gcd（b , a%b）；

时间复杂度 O（log C）；

扩展欧几里得的算法

求 ax + by = gcd（a，b）的一组整数解；

或者判断 ax + by = k 是否有解；

P1516 青蛙的约会

题解：

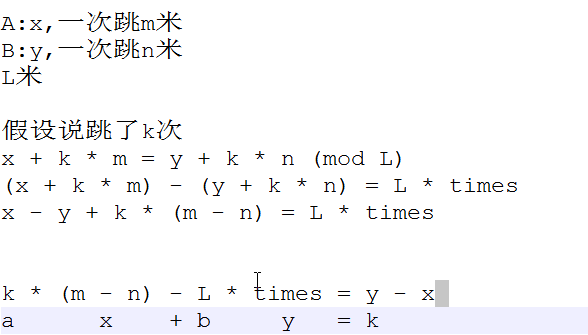
最小公倍数

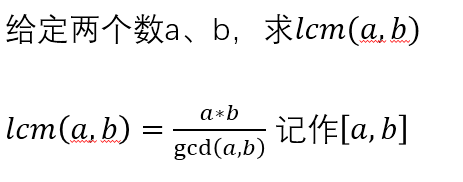
判断素数

给定一个数 n，判断 n 是否为素数；

筛素数

给定一个n，判断 1—n 这 n 个数哪些是素数；

N ≤ 10⁶

用朴素的方法一个一个判断不可行；

只要一个数是某个质因数的 k 倍（k > 1），那么这个数就是合数；

数组 flag 表示每个数是不是素数；

如果一个数是素数，则这个数的倍数都是合数；

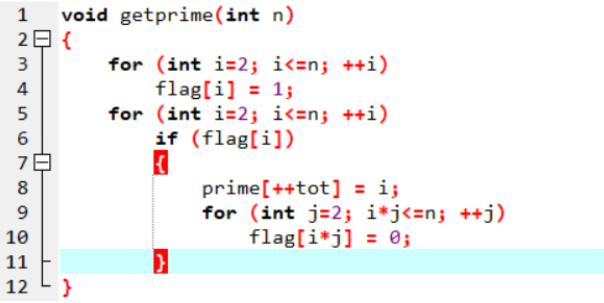
算法复杂度估计：O ( n ) – O ( n log n )；

实际算法复杂度：O ( n loglog n )；

线性筛素数

普通筛素数的方法里，一个合数有可能会被重复筛去多次，因此效率不高；

改进思想：尽量少重复筛素数；

先贴上代码：

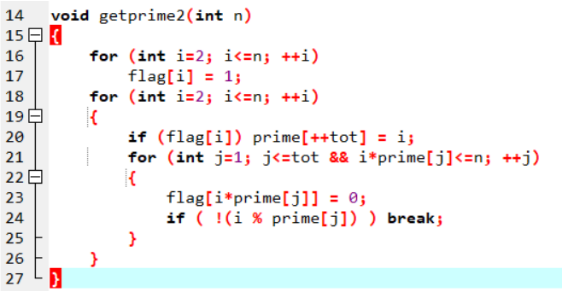
为什么时间复杂度是 O ( n )？

需要证明的东西：

1、我们不会重复删掉一个合数；

2、1~n 的合数都会被我们找出来；

对于一个合数，肯定能表示成：一个数 * 一个小素数 的形式；

因此所有的素数都能被我们筛出来；

算法正确性可以证明；

欧拉函数

欧拉函数：给定数 n，求小于等于 n 中与 n 互素的数的个数；

等价于求 φ ( n )；

等价于求 n 的质因数分解；

O ( √n )；

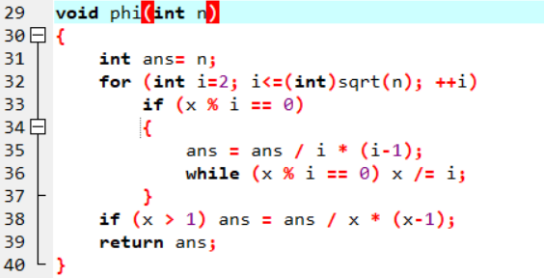
线性求欧拉函数

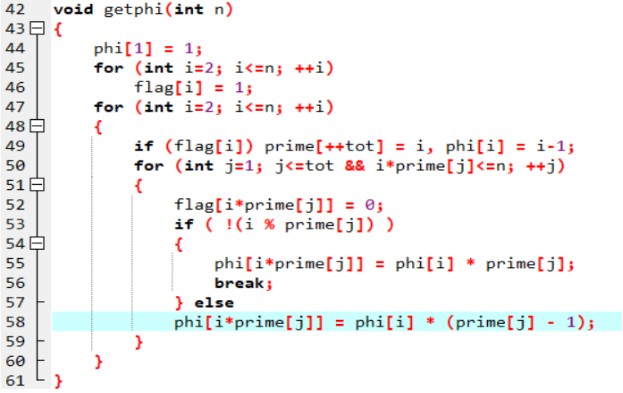
给定一个数 n，要求 1-n 中所有数的欧拉函数；

利用欧拉函数的积性：

性质5：若 a、b 互质，则 φ ( a * b ) = φ ( a ) * φ ( b )；

a % b == 0 , φ ( a * b ) =φ ( a ) * b；

费马小定理&欧拉定理

逆元

求逆元

线性求逆元

给定素数 p，求 1~p-1 中每个数在模 p 意义下的的逆元；

BZOJ 2705 [SDOI2012] Longge的问题

题目描述：Longge 的数学成绩非常好，并且他非常乐于挑战高难度的数学问题。现在问题来了：给定一个整数 N，你需要求出 ∑ gcd ( i , N ) ( 1 <= i <= N )。

对于 60% 的数据，0< N <= 2¹⁶ 。

对于 100% 的数据，0 < N <= 2³² 。

题解：

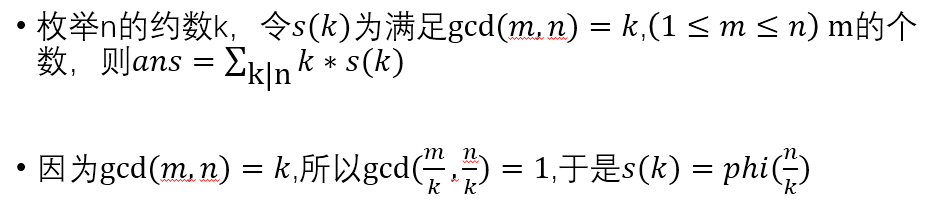
组合数

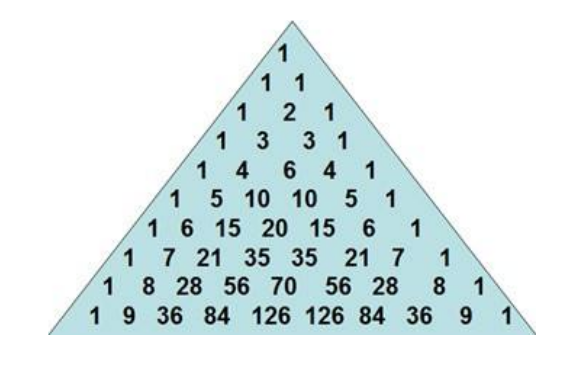
杨辉三角

二项式定理

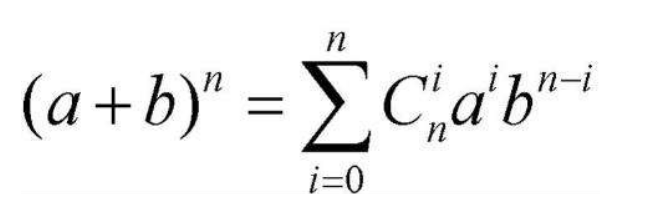
同余

组合数取模：问题一

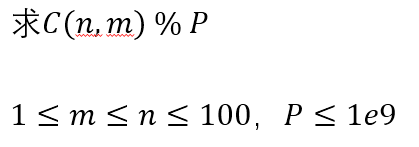
题解：

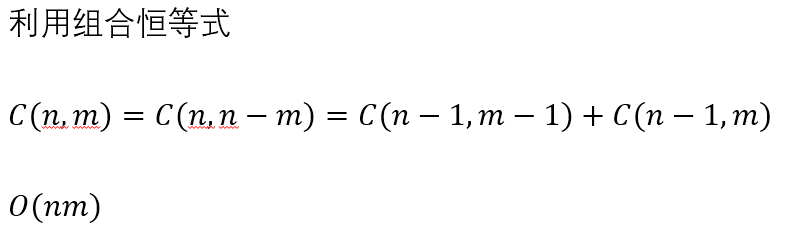
问题二

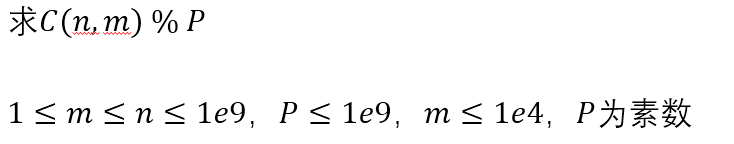
题解：

问题三

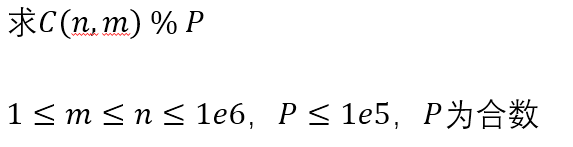
题解：

P 为合数，对于 0~(p-1)，不是每个数都有 ( mod p ) 意义下的逆元；

但是 n , m , p 都不大，考虑组合数的计算式的变形：

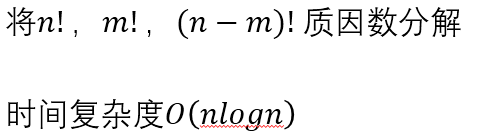
问题四

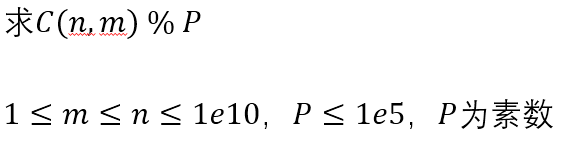
Lucas定理

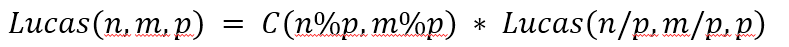
问题五

题解：

Lucas 定理 + 中国剩余定理；

用 Lucas 定理后得到 k 个同余方程；

怎样合并这 k 个同余方程是我们要解决的问题；

中国剩余定理

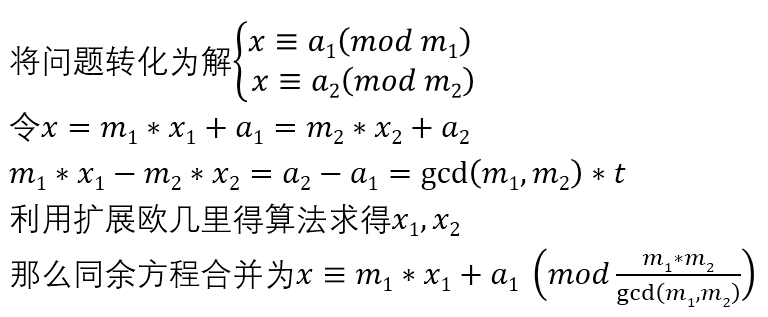
问题六

题解：

扩展卢卡斯定理；

[ZJOI2010]排列计数

题解：

对于一个 n 个元素的二叉堆，其左右儿子为根的对，大小是确定的；

那么设左儿子的对大小为 l，右儿子的对的大小为 r，r = n - l - 1；

为什么是 n - l - 1 呢？因为根也占一个元素；

设 f [ i ] 表示 i 个元素组成的二叉堆的方案数；

f [ n ] = C ( n-1 , l ) * f [ l ] * f [ r ] % p；

若 p 很大，直接做；

若 p 很小，1……p-1 的数是有逆元的；

Lucas 定理，注意 p 必须是素数才能用；

高斯消元

解方程组；

思想：利用加减消元法解方程；

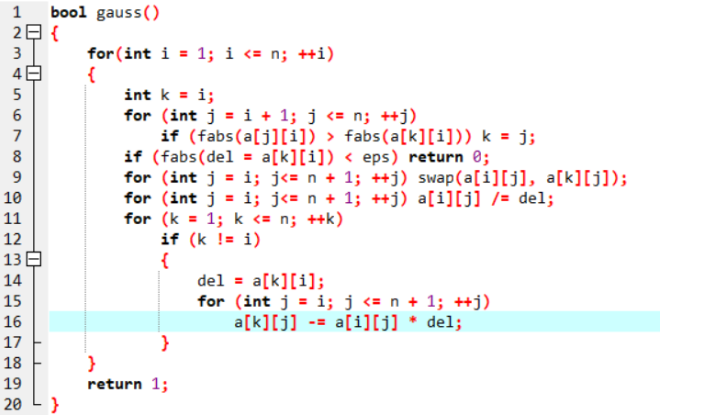
[HNOI2013]游走

题解：

期望走过的次数越大的边，编号越小 ==> 要求总分的期望最小；

每个点的期望经过次数 ==> 求每条边的期望经过次数；

一条边 编号为 k，端点为（x，y）

p [ x ] 表示第 x 个点的期望经过次数；

du [ x ] 表示与 x 相连的点数；

那么低 k 条边的期望经过次数就是 p [ x ] * 1 / du [ x ] + p [ y ] * 1 / du [ y ]；

假设 x 号店与 t₁ , t₂ , t₃ ,..... t_k 相连；

p [ 1 ] = p [ t₁ ] / du [ t₁ ] + p [ t₂ ] / du [ t₂ ] + ...... + p [ t_k ] / du [ t_k ] + 1；

p [ x ] = p [ t₁ ] / du [ t₁ ] + p [ t₂ ] / du [ t₂ ] + ...... + p [ t_k ] / du [ t_k ] ；

有了 n 个方程，n 个未知数，高斯消元；

大步小步算法 

课后作业：Bzoj2242：[SDOI2011]计算器

 

老师的手稿证明过程：

NOIp 会涉及到的数学相关知识：

1. 快速幂；

2. 矩阵乘法；

3. GCD / exGCD；

4. 筛素数 / 素数判断；

5. 欧拉函数 / 质因数分解；

6. 逆元；

7. 组合数问题 / 卢卡斯定理 ；

8. 中国剩余定理；

9. 高斯消元；