极化码之tal-vardy算法（3）

考完驾照，回来填坑 /doge/doge

前两节分别介绍了tal算法中的合并函数和信道操作两个部分，我们将高斯信道的应用放在最后一节来介绍。

　　在之前的介绍中，我们一直在一个前提下进行讨论——即输入字符集是有限的。

　　但是，对于一个具有连续输出字符集的信道，如经典的二元高斯信道，它也可以是对称信道，但是它的输出是连续的，所以不能直接使用tal算法。为了将tal算法应用于改信道，我们就要对这个信道做一些近似。

　　总体思路类似微分思想，将连续输出分成若干个非常小的离散输出。

　　我们假设W为一个具有连续输出的BMS信道，且W满足以下几点：

• W的输出字符集为实数集；
• f(y|0),f(y|1)为输出的概率分布函数，输入为{0,1}；
• W的对称性表现为：f(y|0)=f(-y|1)，y∈R；
• 同时，为了方便起见，我们假设：f(y|0)≥f(y|1)，y≥0。

　　正如我们所期望的那样，BAWGN信道满足上面所有的假设。前两个假设的成立是显然的，对于后两条假设，在BPSK调制下（0映射为1,1映射为-1），我们可以绘制出函数图像。

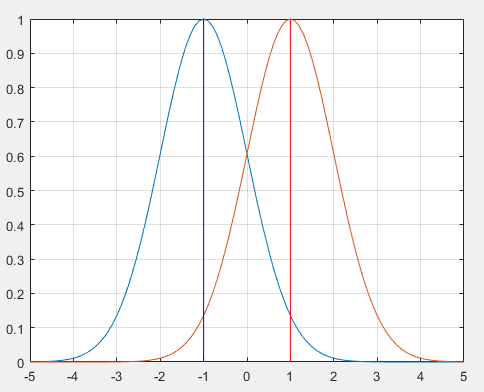图1 高斯曲线对比

　　上图中，高斯曲线的方差均为1，均值分别为1和-1，可以看到，两个曲线关于x = 0是对称的，因此上面第三个假设成立。在x > 0 的区间显然有第四个假设成立。

　　接下来，我们定义y的似然比为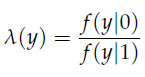：　　根据定义，W的信道容量可以表示为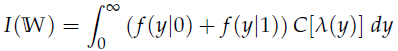：　　其中，在 λ ≥ 1 时，有;　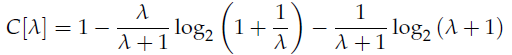　上面这两个公式是从 tal 论文中直接截过来的，由于水平有限，其推导过程我不得而知。

　　作者提到，C[λ] 的一个重要的性质是，它随 λ 的增大呈严格递增。从下图中可以很容易看出这一点：

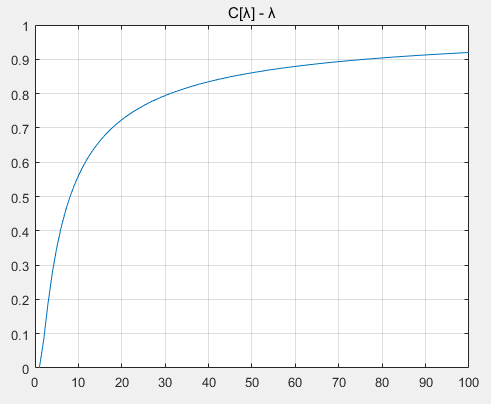图2 C[λ] - λ

　　我们前面已经说过，本节的思路在于通过微分思想，把连续输出近似成为离散输出，而上面的介绍提供了 C[λ] 这样一个参数，我们可以用它来作为分割输出字符集的依据。在论文中，作者是这样进行区分的：

假设 μ=2*v 为指定弱化/强化信道输出字符集，i 取值范围为：1 ≤ i ≤ v-1，那么，可以对输出集 y 作如下分割：其中，第二个不等号在 i 取 i=v 时变为 “≤”。

　　我们看到，在上面这个集合中，y 和 C 之间通过两重映射关系联系到了一起，而 C 被限制在了某个区间之中，因此y也相应的被分割成了若干个小段。

　　下面以弱化操作为例进行讲解：

　　主要内容围绕着Lemma15、Lemma16两个引理展开，在介绍二者之前，需要一些预定义。

　　我们的BMS信道W满足本节最开始的四个假设，定义信道 ，其中，Z定义为：

　　根据定义，我们可以很容易得到Q的信道转移概率表达式，如下，为积分运算：

Lemma15 （在上述定义下的）信道 Q 是一个BMS信道，而且它是 W 的弱化信道：　　

　　这个引理的证明比较容易理解，Q显然是一个BMS信道。只要我们选择中间信道P定义为：　　那么Q是W的弱化信道也是可以理解的。

　Lemma16 Q 和 W 的信道容量之差可以限制在如下区间中:

　　对于 tal 算法在matlab下的实现，可以做如下的介绍。

　　与之前一样，我们的程序设计还是以下面的算法为主要框架：　　在此基础上，对于高斯信道来说，由于它具有连续的输出，因此它的转移概率需要使用上面介绍的积分公式来计算。

　　为了进行积分运算，我们首先需要对 y 进行分区，然后才能在每一个小分区内进行积分。

　　对 y 的分区依据就是上面提到的集合 Ai 。

　　其一、我们可以令 C[λ(y)] = i/v，求出对应的 λ(y)。

　　设 f(x) = C[λ] - i/v，令 f(x) = 0，求得根x的值，由于表达式比较复杂，这一步可以借助使用“牛顿-拉夫逊方法”在matlab上完成，方法见超链接。

　　其二、得到 λ 后，可以根据 λ 与 y 的映射关系，求出 y 。

　　上面内容中， v 是输出单元长度，i 是一个循环下标。i 的循环范围为 1~v，通过 i 的循环和调用上面两个步骤，我们可以得到若干的 y 值，实际上可以把这些 y 值写成向量形式。那么，对于得到的向量，相邻两个元素就是我们求定积分所用到的上下限。

　　得到了高斯信道的近似转移概率，我们就可以将其视为一个离散的BMS信道，接下来，按照前面的思路去进行弱化操作和合并操作，就能够在高斯信道下完成信息位的挑选任务了。