CF1092 --- Tree with Maximum Cost

题干

You are given a tree consisting exactly of $n$ vertices. Tree is a connected undirected graph with $n−1$ edges. Each vertex $v$ of this tree has a value $a_v$ assigned to it.

Let $dist(x,y)$ be the distance between the vertices $x$ and $y$. The distance between the vertices is the number of edges on the simple path between them.

Let's define the cost of the tree as the following value: firstly, let's fix some vertex of the tree. Let it be $v$. Then the cost of the tree is $\sum\limits_{i=1}^{n}dist(i, v)a_i$

Your task is to calculate the maximum possible cost of the tree if you can choose $v$ arbitrarily.

$\mathcal{Input}$

The first line contains one integer $n$, the number of vertices in the tree $(1\leq n\leq 2⋅10^5)$.

The second line of the input contains $n$ integers $a_1,a_2, \cdots ,a_n \; (1\leq a_i\leq 2⋅10^5)$, where $a_i$ is the value of the vertex $i$.

Each of the next $n−1$ lines describes an edge of the tree. Edge $i$ is denoted by two integers $u_i$ and $v_i$, the labels of vertices it connects $(1\leq u_i,v_i\leq n, u_i\not= v_i).$

It is guaranteed that the given edges form a tree.

$\mathcal{Output}$

Print one integer — the maximum possible cost of the tree if you can choose any vertex as $v$.

$\mathcal{Example}$

$Case_1$

$Input$

8

9 4 1 7 10 1 6 5

1 2

2 3

1 4

1 5

5 6

5 7

5 8

$Output$

121

$Case_2$

$Input$

1

1337

$Output$

0

$\mathcal{Note}$

Picture corresponding to the first example:

You can choose the vertex $3$ as a root, then the answer will be $2⋅9+1⋅4+0⋅1+3⋅7+3⋅10+4⋅1+4⋅6+4⋅5=18+4+0+21+30+4+24+20=121$.

In the second example tree consists only of one vertex so the answer is always $0$.

$\mathcal{Tag}$

dfs and similar dp tree *1800

思路分析

本题要求解的是，对于树中所有结点，以该节点为根的情况下计算费用，并求费用的最大值。注意在结点非常多的情况下，要考虑$int$溢出的问题，故开$long\;long$(坑死我了)

暴力想法

暴力想法很简单，很类似CF1324 --- Maximum White Subtree，这里直接搬运那个题解里面的图片

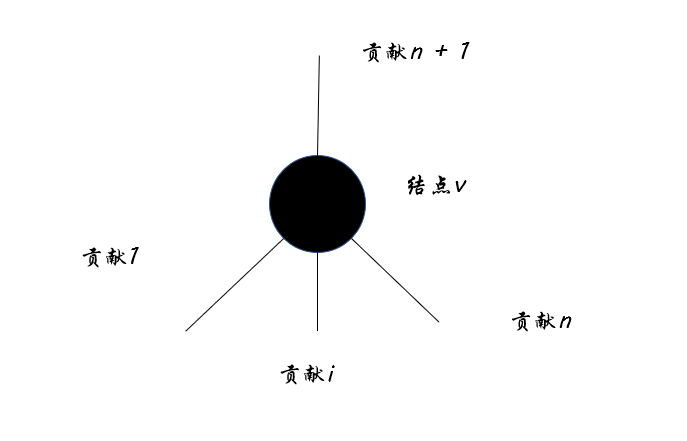
对于任意结点，分别计算不同路径的位置，根据树数据结构的特点，可以把贡献分为:

上层父祖先节点贡献
下层子孙结点贡献

然后就是，如何把暴力$dfs$，通过记忆化实现算法优化。

算法优化

我们先求解下层子孙结点的贡献，通过题目我们知道，从结点$v$转移到结点$u$，其中增量的就是以$v$为根结点，其子树中所有结点值的和。其中$a_i$代表结点$i$的值，我们设$f_i$代表以$i$结点为子树根结点，该子树所有结点的和。我们设$hp_i$代表以$i$结点的下层子孙贡献值,这样我们可以写出下层子孙结点贡献值的转移表达值:

\[f[u] = f[v] + a[u]
\]

\[hp[u] = hp[v] + f[v]
\]

现在我们解决了下层得想办法解决更加困难的上层了，对于这类换根dp问题，常用的手段是用利用父节点的值进行状态转移。在这里我们设$dp_i$为结点$i$的最终费用。因此对于某一节点(非根结点)，该节点的最终费用可以表示为:

\[dp[cur] = dp[fa] - hp[cur] - f[cur] + f[fa] - f[cur] + hp[cur] = dp[fa] + f[fa] - 2*f[cur]
\]

上述表达式的意思为:父节点刨去结点$cur$的费用值($dp[fa] - hp[cur] - f[cur]$，加上增量($f[fa] - f[cur]$, note 这里的f[fa],代表着所有的结点和)，再最后加上下层子孙结点贡献值($hp[cur]$).

\[dp[v] = \left\{\begin{array}
1hp[v] & if\; v = root \\
dp[fa] + f[fa] - 2*f[v] & if\; v \not= root\\
\end{array}\right.
\]

&emps;因此我们最终的思路还是为:

从下往上树形$dp$,计算$f_v$,$hp_v$
从上往下换根$dp$,计算$dp_v$

代码

#include<bits/stdc++.h>

using namespace std;

using LL = long long;

using  VL = vector<LL>;

using  VVL = vector<VL>;

LL mx = 0x8000000000000000;

VL a, f, hp, dp;

VVL e;

void dfs(int x, int fa = -1)

{

    f[x] =  a[x], hp[x] = 0;

    for (auto to : e[x])

    {

        if (to == fa) continue;

        dfs(to, x);

        f[x] += f[to];

        hp[x] += (hp[to] + f[to]);

    }

}

void rdfs(int x, int fa = -1)

{

    dp[x] = hp[x];

    mx = max(mx, dp[x]);

    for (auto to : e[x])

    {

        if (to == fa) continue;

        hp[to] = dp[x] + f[x] - 2*f[to];

        f[to] = f[x];

        rdfs(to, x);

    }

}

int main()

{

    int n;

    cin >> n;

    a = f = hp = dp = VL(n);

    e = VVL(n);

    for (auto &x : a) cin >> x;

    for (int i = 0; i < n - 1; ++ i)

    {

        int x, y;

        cin >> x >> y;

        -- x, -- y;

        e[x].push_back(y);

        e[y].push_back(x);

    }

    dfs(0);

    rdfs(0);

    cout << mx << endl;

    return 0;

}

做了两次了，这个1092是自己手打的，还是有进步。WA了一次是没有考虑到整数溢出的情况以后得多加考虑。

以后对于每个根结点都要求的题，考虑优先换根dp。