Estimating Gene Frequencies| method of maximum likelihood|point estimate
I.11 Estimating Gene Frequencies
在小样本上计算基因A的概率PA,举例如下:

通过加大样本会将通过观察值得到的数趋近于真实数据,所以该问题转化为了统计学上利用大量观察值求真实值的问题,因此通过最大似然估计得到真实值.
为了理解多项式分布可以先以二项分布为例:

该二项分布来自:
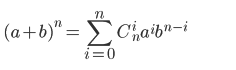
其实它的完整形式是:
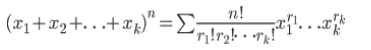
因为二项分布是当多项式分布的项数为2时的分布:

所以当有三项(AA,Aa,aa)的时候我们采用多项式分布:于是就有

其中,p就是PA,就是我们估计的参数,nAA,nAa,naa是给定值。
由于组合数是一个常数,用C代替,得到:
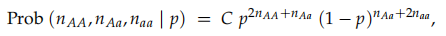
此时,采用最大似然估计,(即找到使概率值最大的参数p,即将p的表达式对p求导,然后导数为零时,便有最大函数值(概率值)。)
为方便求导两边取对数:
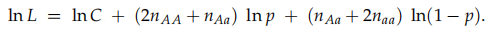
求导:

化简后得到:
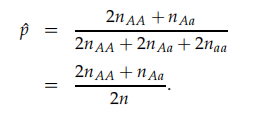
Estimating Gene Frequencies| method of maximum likelihood|point estimate的更多相关文章
- Maximum Likelihood及Maximum Likelihood Estimation
1.What is Maximum Likelihood? 极大似然是一种找到最可能解释一组观测数据的函数的方法. Maximum Likelihood is a way to find the mo ...
- Maximum Likelihood Method最大似然法
最大似然法,英文名称是Maximum Likelihood Method,在统计中应用很广.这个方法的思想最早由高斯提出来,后来由菲舍加以推广并命名. 最大似然法是要解决这样一个问题:给定一组数据和一 ...
- 最大似然估计实例 | Fitting a Model by Maximum Likelihood (MLE)
参考:Fitting a Model by Maximum Likelihood 最大似然估计是用于估计模型参数的,首先我们必须选定一个模型,然后比对有给定的数据集,然后构建一个联合概率函数,因为给定 ...
- MLE vs MAP: the connection between Maximum Likelihood and Maximum A Posteriori Estimation
Reference:MLE vs MAP. Maximum Likelihood Estimation (MLE) and Maximum A Posteriori (MAP), are both a ...
- Linear Regression and Maximum Likelihood Estimation
Imagination is an outcome of what you learned. If you can imagine the world, that means you have lea ...
- 似然函数 | 最大似然估计 | likelihood | maximum likelihood estimation | R代码
学贝叶斯方法时绕不过去的一个问题,现在系统地总结一下. 之前过于纠结字眼,似然和概率到底有什么区别?以及这一个奇妙的对等关系(其实连续才是f,离散就是p). 似然函数 | 似然值 wiki:在数理统计 ...
- 最大似然估计(Maximum Likelihood,ML)
先不要想其他的,首先要在大脑里形成概念! 最大似然估计是什么意思?呵呵,完全不懂字面意思,似然是个啥啊?其实似然是likelihood的文言翻译,就是可能性的意思,所以Maximum Likeliho ...
- Maximum likelihood from incomplete data via the EM algorithm (1977)
Maximum likelihood from incomplete data via the EM algorithm (1977)
- [Bayes] Maximum Likelihood estimates for text classification
Naïve Bayes Classifier. We will use, specifically, the Bernoulli-Dirichlet model for text classifica ...
随机推荐
- JavaScript 之 异步请求
一. 1.异步(async) 异步,它的孪生兄弟--同步(Synchronous),"同步模式"就是上一段的模式,后一个任务等待前一个任务结束,然后再执行,程序的执行顺序与任务的排 ...
- JAVA初学者——Hello,World!
大家好,我是浩宇大熊猫 我本科专业学的是GIS(Geographical Information System),大学期间也学习了很多的编程语言,有C/C++/JAVA等 之前给我们授课的是韩冰老师, ...
- Mac OS 终端利器 iTerm2配置大全
之前一直使用 Mac OS 自带的终端,用起来虽然有些不太方便,但总体来说还是可以接受的,是有想换个终端的想法,然后今天偶然看到一个终端利器 iTerm2,发现真的很强大,也非常的好用,按照网上配置了 ...
- linux上大文件切割成小文件传输
使用tar命令进行压缩,使用split进行切割 压缩并分割: tar -zcvf - admin- |split -b 100m -d admin-.tar.gz 解压: 先合并成tar包在解压 ca ...
- (函数)P1217 [USACO1.5]回文质数 Prime Palindromes
题解: 第一次: 算法复杂度过高,导致编译超时,需要优化 #include<stdio.h>#include<math.h>int a[100000001] = { 0 };i ...
- 面试准备 css 书写顺序及原理
书写顺序 (1)定位属性:position display float left top right bottom overflow clear z-index (2)自身属性: ...
- Html4.0.1 标签使用笔记
1.lang=zh,en有什么用? 告诉搜索引擎爬虫,网站是关于什么内容的,优先显示网站排名.一般竞价排名,根据百度搜索引擎,需要签订关键词协议,首页第一个竞价排名大概是30-50元/条,竞价排名范围 ...
- python学习笔记-函数与可变长参数
一.函数 1. def test(x): y=x+1 return yprint(test) #这是打印函数在内存中的地址 过程:就是没有返回值的函数 在python中过程也是函数,就算没哟返回值,也 ...
- keras猫狗大战
先划分数据集程序训练集中猫狗各12500张现在提取1000张做为训练集,500张作为测试集,500张作为验证集: # -*- coding: utf-8 -*-import os, shutil or ...
- redis day03 下
事务 能够有回退状态 事务命令 安命令执行没问题,redis是弱事务型 nulti incr n1 -->QUEUED(返回仅队列了) EXEC -->返回结果 pipeline 流水 ...
