自适应线性神经网络Adaline

自适应线性神经网络Adaptive linear network， 是神经网络的入门级别网络。

相对于感知器，

1. 采用了f（z）=z的激活函数，属于连续函数。
2. 代价函数为LMS函数，最小均方算法，Least mean square。

实现上，采用随机梯度下降，由于更新的随机性，运行多次结果是不同的。

 '''
 Adaline classifier

 created on 2019.9.14
 author: vince
 '''
 import pandas
 import math
 import numpy
 import logging
 import random
 import matplotlib.pyplot as plt

 from sklearn.datasets import load_iris
 from sklearn.model_selection import train_test_split
 from sklearn.metrics import accuracy_score

 '''
 Adaline classifier

 Attributes
 w: ld-array = weights after training
 l: list = number of misclassification during each iteration
 '''
 class Adaline:
     def __init__(self, eta = 0.001, iter_num = 500, batch_size = 1):
         '''
         eta: float = learning rate (between 0.0 and 1.0).
         iter_num: int = iteration over the training dataset.
         batch_size: int = gradient descent batch number,
             if batch_size == 1, used SGD;
             if batch_size == 0, use BGD;
             else MBGD;
         '''

         self.eta = eta;
         self.iter_num = iter_num;
         self.batch_size = batch_size;

     def train(self, X, Y):
         '''
         train training data.
         X:{array-like}, shape=[n_samples, n_features] = Training vectors,
             where n_samples is the number of training samples and
             n_features is the number of features.
         Y:{array-like}, share=[n_samples] = traget values.
         '''
         self.w = numpy.zeros(1 + X.shape[1]);
         self.l = numpy.zeros(self.iter_num);
         for iter_index  in range(self.iter_num):
             for rand_time in range(X.shape[0]):
                 sample_index = random.randint(0, X.shape[0] - 1);
                 if (self.activation(X[sample_index]) == Y[sample_index]):
                     continue;
                 output = self.net_input(X[sample_index]);
                 errors = Y[sample_index] - output;
                 self.w[0] += self.eta * errors;
                 self.w[1:] += self.eta * numpy.dot(errors, X[sample_index]);
                 break;
             for sample_index in range(X.shape[0]):
                 self.l[iter_index] += (Y[sample_index] - self.net_input(X[sample_index])) ** 2 * 0.5;
             logging.info("iter %s: w0(%s), w1(%s), w2(%s), l(%s)" %
                     (iter_index, self.w[0], self.w[1], self.w[2], self.l[iter_index]));
             if iter_index > 1 and math.fabs(self.l[iter_index - 1] - self.l[iter_index]) < 0.0001:
                 break;

     def activation(self, x):
         return numpy.where(self.net_input(x) >= 0.0 , 1 , -1);

     def net_input(self, x):
         return numpy.dot(x, self.w[1:]) + self.w[0];

     def predict(self, x):
         return self.activation(x);

 def main():
     logging.basicConfig(level = logging.INFO,
             format = '%(asctime)s %(filename)s[line:%(lineno)d] %(levelname)s %(message)s',
             datefmt = '%a, %d %b %Y %H:%M:%S');

     iris = load_iris();

     features = iris.data[:99, [0, 2]];
     # normalization
     features_std = numpy.copy(features);
     for i in range(features.shape[1]):
         features_std[:, i] = (features_std[:, i] - features[:, i].mean()) / features[:, i].std();

     labels = numpy.where(iris.target[:99] == 0, -1, 1);

     # 2/3 data from training, 1/3 data for testing
     train_features, test_features, train_labels, test_labels = train_test_split(
             features_std, labels, test_size = 0.33, random_state = 23323);

     logging.info("train set shape:%s"  % (str(train_features.shape)));

     classifier = Adaline();

     classifier.train(train_features, train_labels);

     test_predict = numpy.array([]);
     for feature in test_features:
         predict_label = classifier.predict(feature);
         test_predict = numpy.append(test_predict, predict_label);

     score = accuracy_score(test_labels, test_predict);
     logging.info("The accruacy score is: %s "% (str(score)));

     #plot
     x_min, x_max = train_features[:, 0].min() - 1, train_features[:, 0].max() + 1;
     y_min, y_max = train_features[:, 1].min() - 1, train_features[:, 1].max() + 1;
     plt.xlim(x_min, x_max);
     plt.ylim(y_min, y_max);
     plt.xlabel("width");
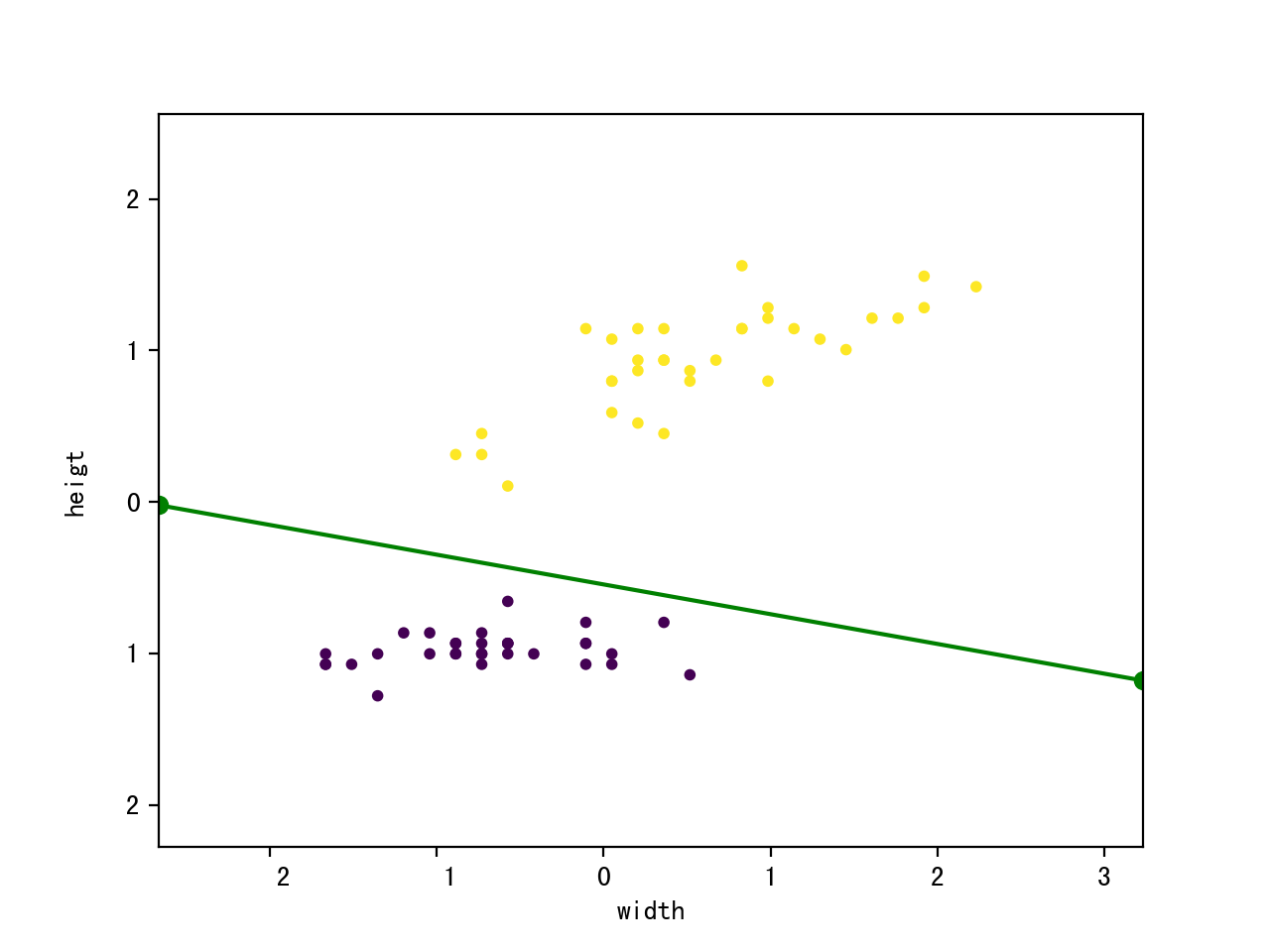
     plt.ylabel("heigt");

     plt.scatter(train_features[:, 0], train_features[:, 1], c = train_labels, marker = 'o', s = 10);

     k = - classifier.w[1] / classifier.w[2];
     d = - classifier.w[0] / classifier.w[2];

     plt.plot([x_min, x_max], [k * x_min + d, k * x_max + d], "go-");

     plt.show();

 if __name__ == "__main__":
     main();