【cs224w】Lecture 5 - 谱聚类

Spectral Clustering

前面的课程说到了 community detection 并介绍了两种算法。这次来说说另外一类做社区聚类的算法，谱聚类。这种算法一般分为三个步骤

1. pre-processing: 构建一个描述图结构的矩阵
2. decomposition: 通过特征值和特征向量分解矩阵
3. grouping: 基于分解后的矩阵以及点的 representation 进行聚类

在介绍具体操作前我们先了解几个概念

Graph Partitioning

图的划分就是将节点分到不同的组内，如果分为两个组就是二分。划分的目的其实就是找社区，那如何判断一个划分的质量呢？回顾之前说到的社区的特点，即社区内部连接丰富而社区间连接稀疏。因此我们希望我们的划分能最大化每个划分内的连接并最小化划分间的连接数。我们用割这个概念来描述不同划分间的连接数 \(cut(A,B)=\sum\limits_{i\in A,j\in B}w_{ij}\)。对于无权图这里的 \(w\) 就是 \(\{0,1\}\)。但这个定义并不完美，因为这样并不能保证划分均匀。例如，一个图中有一个节点的度为 \(1\) 那么只要把这个节点和其余节点分开就能保证 cut 为 \(1\)。因此我们将划分后不同组内节点的度纳入考虑就能较为全面的评估一个划分的好坏了，即 Conductance，其中 \(vol\) 是划分内所有节点的度之和。

\[\phi(A,B)=\frac{cut(A,B)}{\min(vol(A),vol(B))}
\]

然而直接最小化 conductance 是个 NP-hard 的问题。那接下来就进入今天的正题：谱聚类。

---

首先复习一下线性代数，给定一个图的邻接矩阵 \(A\)，那 \(i\) 行表示节点 \(i\) 的所有出度，\(j\) 列表示节点 \(j\) 的所有入度。在无向图上出度入度一样，因此 \(A^T=A\)，。考虑无向图，那 \(Ax\) 代表什么？\(Ax\) 的输出是一个向量，而向量的每一个元素是矩阵的行和向量 \(x\) 的内积。如果将 \(x\) 看作图中每个节点的分类标签，那得到的结果向量的每个元素代表了每个节点所有邻接节点的标签之和。

而特征值的定义是 \(Ax=\lambda x\)，而谱聚类就是研究根据特征值 \(\lambda\) 升序排序后的特征向量。(这里规定 \(\Lambda=\{\lambda_1,\lambda_2,...,\lambda_n\}\) 且 \(\lambda_1\leq\lambda_2 \leq...\leq\lambda_n\))

\(d\)-Regular Graph

现在给出一个特殊的连通图 \(G\)，图中所有节点的度都为 \(d\)。然后令 \(x=(1,1,...,1)\) 那么 \(Ax=(d,d,...,d)=\lambda x\)，因此 \(\lambda=d\)。可以证明 \(d\) 是最大的特征值。

证明：

因为我们希望特征值为 \(d\)，那对向量 \(x\) 必须有 \(x_i=x_j\)。也就是说 \(x=c\cdot(1,1,...,1)\)

那么对于任意不满足 \(c\cdot(1,1,...,1)\) 的向量 \(y\)，说明并非所有节点都为 \(1\)。令不为 \(1\) 的节点集为 \(S\)，显然并非所有节点都在 \(S\) 中。

这样一来必定存在节点 \(j\)，其邻接节点不属于 \(S\)。这样一来在节点 \(j\) 这里得到的内积值必定严格小于 \(d\)

因此 \(y\) 不是特征向量，且 \(d\) 是最大的特征值

以上是针对连通图。如果图不连通而是有两个部分，且每部分都是 \(d\)-regular 的。我们做类似处理，不过对 \(x\) 的定义会适当改变。

\[\begin{cases}
x'=(1,...,1,0,...,0)^T, Ax'=(d,...,d,0,...,0)^T \\
x''=(0,...,0,1,...,1)^T, Ax''=(0,...,0,d,...,d)^T
\end{cases}\]

这样一来对应的特征值仍然是 \(\lambda=d\)，但这个最大特征值对应了两个特征向量。

为什么不继续用 \(x=(1,1,...,1)^T\)？

你试试 \(Ax=\lambda x\) 对得上不？

如下图稍微推广一下，第一种不连通情况下，最大和第二大的特征值相等。第二种情况属于存在明显社区结构，此时图其实是连通的，但最大和第二大的特征值差别不大。而 \(\lambda_{n-1}\) 能告诉我们两个社区的划分情况。

那为什么说 \(\lambda_{n-1}\) 能告诉我们划分情况？首先我们知道特征向量是互相垂直的，即两个特征向量的内积为 \(0\)。因此在已知 \(x_n=(1,1,...,1)^T\) 的情况下，\(x_nx_{n-1}=0\) 说明 \(\sum_ix_{n-1}[i]=0\)。因此，在 \(x_{n=1}\) 内必定有正有负。那我们就可以依此将图中的节点分为两组了。(这是大致思路，还有很多细节需要考虑)

那考虑无向图，我们定义以下几个矩阵

1. 邻接矩阵 \(A\)
   • 对称
   • \(n\) 个实数特征值
   • 特征向量为实数且互相垂直
2. 度矩阵 \(D\)
   • 对角矩阵
3. 拉普拉斯矩阵 \(L=D-A\)
   • 半正定
   • 特征值为非负实数
   • 特征向量为实数且互相垂直
   • 对所有 \(x\) 有 \(x^TLx=\sum_{ij}L_{ij}x_ix_j\geq 0\)

这里有个定理：对任意对称矩阵 \(M\) 有

\[\lambda_2=\min\limits_{x:x^Tw_1=0}\frac{x^TMx}{x^Tx}
\]

\(w_1\) 是最小特征值对应的特征向量。分析一下这个表达式

\[\begin{aligned}
x^TLx&=\sum\limits_{i,j=1}^nL_{ij}x_ix_j=\sum\limits_{i,j=1}^n(D_{ij}-A_{ij})x_ix_j \\
&=\sum_iD_{ii}x_i^2-\sum_{(i,j)\in E}2x_ix_j \\
&=\sum_{(i,j)\in E}(x_i^2+x_j^2-2x_ix_j) \\
&=\sum_{(i,j)\in E}(x_i-x_j)^2
\end{aligned}\]

因为度矩阵 \(D\) 是对角矩阵，所以上面才会化简为 \(D_{ii}\)。 因为这里的求和是针对每条边，而每条边有两个端点，因此第三步是 \(x_i^2+x_j^2\)。化简了定理里的表达式能看出什么？\(\lambda_2\) 是特征向量里各元素的差的平方(距离)的最小值。这与我们找最小割目的不谋而合，即最小化各部分间的连接数。



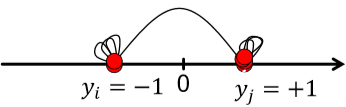
这样得到的 \(x\) 叫 Fiedler vector。然而直接用离散的标签 \(\{-1,1\}\) 太硬核了，我们考虑允许 \(x\) 为满足约束的实数。即 \(\sum_ix_i=0, \sum_ix_i^2=1\)

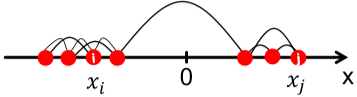
其实这里偷换了概念。表达式里应该将 \(x\) 替换为 \(y\)。因为分析的时候我们将 \(y\) 视为划分后的标签，而特征值 \(x_2\) 只是这个标签 \(y\) 的最优解而已。

这里提到了 approx. guarantee，如果将网络划分为 \(A\) 和 \(B\)，那可以保证 \(\lambda_2\) 和 conductance \(\beta\) 存在关系 \(\lambda_2\leq2\beta\) (证明略，自己看 slide 吧)

---

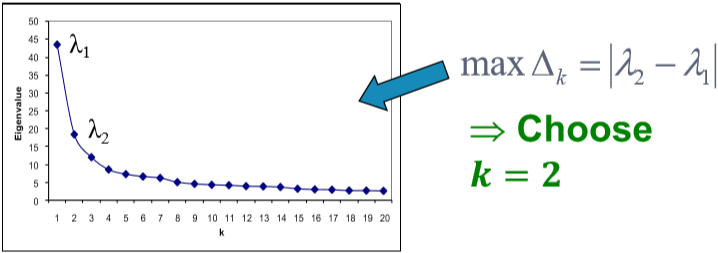
根据这种方法得到的结果还是不错的。如果网络中包含了不止一个划分，我们可以递归地使用上述算法，即先划分为两部分，然后对两部分分别再用使用一次或多次谱聚类。除此之外还可以使用 \(x_3,x_4,...\) 等特征向量一起进行聚类，这样一来相当于将每个点表示为 \(k\) 维的向量进行聚类。一般来说多用几个特征向量能避免信息丢失，得到更好的聚类结果。那这个 \(k\) 怎么选呢？看 \(\Delta_k=|\lambda_k-\lambda_{k-1}|\)。选令 eigengap 最大的 \(k\) 就好。(注意！！这里的特征值又是按降序排列的了)^[1]

Motif-Based Spectral Clustering

上面的谱聚类是基于边实现的，如果我们想针对某种特定的结构进行划分呢？自然而然的想到之前介绍的 motif。基于 motif 也就是说在一个划分内特定的 motif 普遍出现。类似对边的划分，我们定义 \(vol_M(S)\) 为在划分 \(S\) 里的 motif 的端点个数，\(\phi(S)=\frac{\#(motifs\ cut)}{vol_M(S)}\)。当然这也是 NP-hard 的。

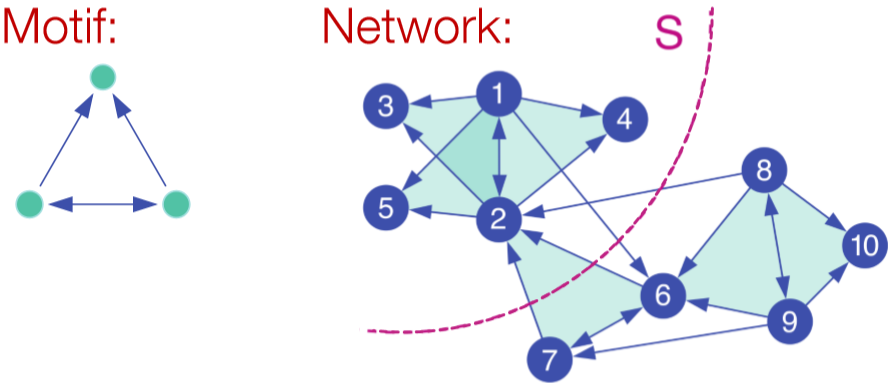
走流程，首先我们需要定义矩阵 \(W^{(M)}\)。这里矩阵内每个元素代表了对应边被几个 motif 共享。然后是度矩阵 \(D^{(M)}=\sum_jW_{ij}^{(M)}\) 和拉普拉斯矩阵 \(L^{(M)}=D^{(M)}-W^{(M)}\)。求特征值和特征向量后取第二小的特征值对应的特征向量 \(x_2\)。按升序对 \(x_2\) 各元素大小排序，并依次通过计算 motif conductance 来找最佳的划分。(前 \(k\) 小的元素为 \(x_2^{(1)},x_2^{(2)},...,x_2^{(k)}\)，然后计算 conductance。取令 conductance 最小的 \(k\) 值)^[2]

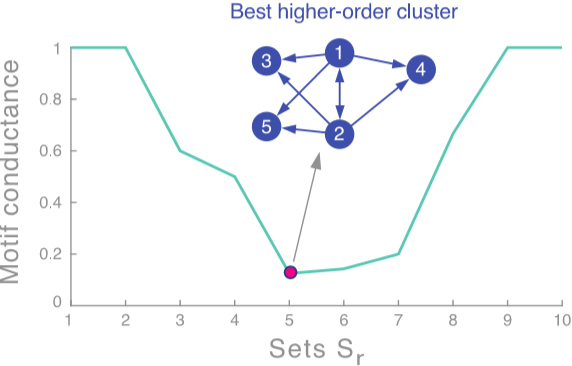
当然这个算法也只是一个近似，它能保证 \(\phi_M(S)\leq4\sqrt{\phi_M^*}\)

---

1. 虽然选最大的 gap 是 make sense 的。但要说个所以然还是有点讲不清楚，需要再理解理解。 ↩︎

2. 这个方法叫 sweep procedure，不同于之前以 \(0\) 为界的划分。那 motif-based 能用之前的方法吗？sweep procedure 有什么优势吗？基于边的谱聚类能用 sweep procedure 吗？ ↩︎