洛谷3388 tarjan割点

题目链接：https://www.luogu.com.cn/problem/P3388

tarjan算法果然牛逼，时间复杂度是O(|V|+|E|)，所以1e4个结点2e5条边的图完全不在话下orz orz

一个无向图求割点，该图不一定连通，所以要对没有访问过的点继续tarjan，这时候我就wa了几次，因为之前只用过一次tarjan，在参数设置里面我默认了从u=1开始建dfs树。每次只有根节点的father值等于其编号，这样就能唯一地标识它，学到了。其次在下面证明 tarjan中如果在处理回退边的时候用的是①、 low[u]=min(low[u],low[v])（强连通分量的用法）而不是②、low[u]=min(low[u],dfn[v])的话将会出现什么样的错误。

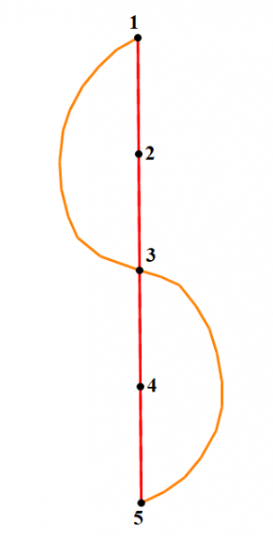
我们模拟两种Tarjan算法，一种是low[u] = min( low[u], low[v] );，一种是low[u] = min( low[u], dfn[v] );。（证明参考洛谷博客）

第1种：

① dfs(1)，dfn[1] = 1，low[1] = 1。

② dfs(2)，dfn[2] = 2，low[2] = 2。

③ dfs(3)，dfn[3] = 3，low[3] = 3。

④ 发现回边 3 -> 1，low[3] = 1。

⑤ dfs(4)，dfn[4] = 4，low[4] = 4。

⑥ dfs(5)，dfn[5] = 5，low[5] = 5。

⑦ 发现回边 5 -> 3，low[5] = 1。

⑧ dfs(5)结束，回到dfs(4)，low[4] = 1。

⑨ dfs(4)结束，回到dfs(3)，low[3] = 1。

⑩ dfs(3)结束，至此未发现割点。

第2种：

① dfs(1)，dfn[1] = 1，low[1] = 1。

② dfs(2)，dfn[2] = 2，low[2] = 2。

③ dfs(3)，dfn[3] = 3，low[3] = 3。

④ 发现回边 3 -> 1，low[3] = 1。

⑤ dfs(4)，dfn[4] = 4，low[4] = 4。

⑥ dfs(5)，dfn[5] = 5，low[5] = 5。

⑦ 发现回边 5 -> 3，low[5] = 3。

⑧ dfs(5)结束，回到dfs(4)，low[4] = 3。

⑨ dfs(4)结束，回到dfs(3)，low[4] >= dfn[3]，发现割点3，low[3] = 1。

而这个图中，正确答案是：3是割点。

所以第1种方法就被我们愉快地Hack掉了。

其次，我在处理回退边的时候在条件中加上了dfn[v]<dfn[u]，时间效率提高了大约10%，这是显而易见的，因为只有回退边到达的结点在父节点之前被访问，而且这个结点还不是已经处理过的fa结点。

代码如下：

 #include<bits/stdc++.h>
 using namespace std;
 typedef unsigned int ui;
 typedef long long ll;
 typedef unsigned long long ull;
 #define pf printf
 #define mem(a,b) memset(a,b,sizeof(a))
 #define prime1 1e9+7
 #define prime2 1e9+9
 #define pi 3.14159265
 #define lson l,mid,rt<<1
 #define rson mid+1,r,rt<<1|1
 #define scand(x) scanf("%llf",&x)
 #define f(i,a,b) for(int i=a;i<=b;i++)
 #define scan(a) scanf("%d",&a)
 #define mp(a,b) make_pair((a),(b))
 #define P pair<int,int>
 #define dbg(args) cout<<#args<<":"<<args<<endl;
 #define inf 0x3f3f3f3f
 const int maxn=2e4+;
 int n,m,t;
 inline int read(){
     int ans=,w=;
     char ch=getchar();
     while(!isdigit(ch)){if(ch=='-')w=-;ch=getchar();}
     while(isdigit(ch))ans=(ans<<)+(ans<<)+ch-'',ch=getchar();
     return ans*w;
 }
 int low[maxn],dfn[maxn],iscut[maxn],head[maxn],nxt[];
 int cnt=;
 int ans=;
 struct node{
     int u,v;
 }p[];
 int e=;
 void addedge(int x,int y)
 {
     p[e].u=x;
     p[e].v=y;
     nxt[e]=head[x];
     head[x]=e++;
 }
 void tarjan(int u,int fa)
 {
     dfn[u]=low[u]=++cnt;
     int child=;
     for(int i=head[u];~i;i=nxt[i])
     {
         int v=p[i].v;
         if(!dfn[v])
         {
             if(fa==u)child++;
             tarjan(v,u);
             low[u]=min(low[v],low[u]);
             if(low[v]>=dfn[u]&&u!=fa)iscut[u]=;
         }
         else if(dfn[v]<dfn[u]&&v!=fa)
         {
             low[u]=min(low[u],dfn[v]);
         }
     }
     if(u==fa&&child>)iscut[u]=;
 }
 int main()
 {
     //freopen("input.txt","r",stdin);
     //freopen("output.txt","w",stdout);
     std::ios::sync_with_stdio(false);
     n=read(),m=read();
     int x,y;
     cnt=;
     ans=;
     mem(low,);
     mem(dfn,);
     mem(iscut,);
     mem(head,-);
     mem(nxt,-);
     f(i,,m)
     {
         x=read(),y=read();
         addedge(x,y);
         addedge(y,x);
      }
      f(i,,n)
      {
          if(!dfn[i])tarjan(i,i);//图不一定连通，所以每个连通分量都要tarjan一次
       }
      f(i,,n)
      {
          if(iscut[i])ans++;
      }
      pf("%d\n",ans);
      f(i,,n)
      if(iscut[i])pf("%d ",i);
      return ;
 }