九、深度优先 && 广度优先

原文地址

一、什么是“搜索”算法？

• 算法是作用于具体数据结构之上的，深度优先搜索算法和广度优先搜索算法都是基于“图”这种数据结构的。
• 因为图这种数据结构的表达能力很强，大部分涉及搜索的场景都可以抽象成“图”。
• 图上的搜索算法，最直接的理解就是，在图中找出从一个顶点出发，到另一个顶点的路径。
• 具体方法有很多，两种最简单、最“暴力”的方法为深度优先、广度优先搜索，还有A、 IDA等启发式搜索算法。
• 图有两种主要存储方法，邻接表和邻接矩阵。
• 以无向图，采用邻接表存储为例：

public class Graph {
    // 顶点的个数
    private int v;
    // 每个顶点后面有个链表
    private LinkedList<Integer>[] adj;

    public Graph(int v) {
        this.v = v;
        adj = new LinkedList[v];
        for (int i = 0; i < v; i++) {
            adj[i] = new LinkedList<>();
        }
    }

    /**
     * 添加边
     * @param s 顶点
     * @param t 顶点
     */
    public void addEdge(int s,int t){
        // 无向图一条边存两次（联想微信好友）
        adj[s].add(t);
        adj[t].add(s);
    }
}

二、广度优先搜索（BFS）

• 广度优先搜索（Breadth-First-Search），简称为 BFS。
• 它是一种“地毯式”层层推进的搜索策略，即先查找离起始顶点最近的，然后是次近的，依次往外搜索。
• 

2.1、实现过程

/**
 * 图的广度优先搜索，搜索一条从 s 到 t 的路径。
 * 这样求得的路径就是从 s 到 t 的最短路径。
 *
 * @param s 起始顶点
 * @param t 终止顶点
 */
public void bfs(int s, int t) {
    if (s == t) {
        return;
    }
    // visited 记录已经被访问的顶点，避免顶点被重复访问。如果顶点 q 被访问，那相应的visited[q]会被设置为true。
    boolean[] visited = new boolean[v];
    visited[s] = true;
    // queue 是一个队列，用来存储已经被访问、但相连的顶点还没有被访问的顶点。因为广度优先搜索是逐层访问的，只有把第k层的顶点都访问完成之后，才能访问第k+1层的顶点。
    // 当访问到第k层的顶点的时候，需要把第k层的顶点记录下来，稍后才能通过第k层的顶点来找第k+1层的顶点。
    // 所以，用这个队列来实现记录的功能。
    Queue<Integer> queue = new LinkedList<>();
    queue.add(s);
    // prev 用来记录搜索路径。当从顶点s开始，广度优先搜索到顶点t后，prev数组中存储的就是搜索的路径。
    // 不过，这个路径是反向存储的。prev[w]存储的是，顶点w是从哪个前驱顶点遍历过来的。
    // 比如，通过顶点2的邻接表访问到顶点3，那prev[3]就等于2。为了正向打印出路径，需要递归地来打印，就是print()函数的实现方式。
    int[] prev = Arrays.stream(new int[v]).map(f -> -1).toArray();

    while (queue.size() != 0) {
        int w = queue.poll();
        LinkedList<Integer> wLinked = adj[w]; // 表示：邻接表存储时顶点为w，所对应的链表
        for (int i = 0; i < wLinked.size(); ++i) {
            int q = wLinked.get(i);
            // 判断顶点 q 是否被访问
            if (!visited[q]) {
                // 未被访问
                prev[q] = w;
                if (q == t) {
                    print(prev, s, t);
                    return;
                }
                visited[q] = true;
                queue.add(q);
            }
        }
    }
}

// 递归打印s->t的路径
private void print(int[] prev, int s, int t) {
    if (prev[t] != -1 && t != s) {
        print(prev, s, prev[t]);
    }
    System.out.print(t + " ");
}

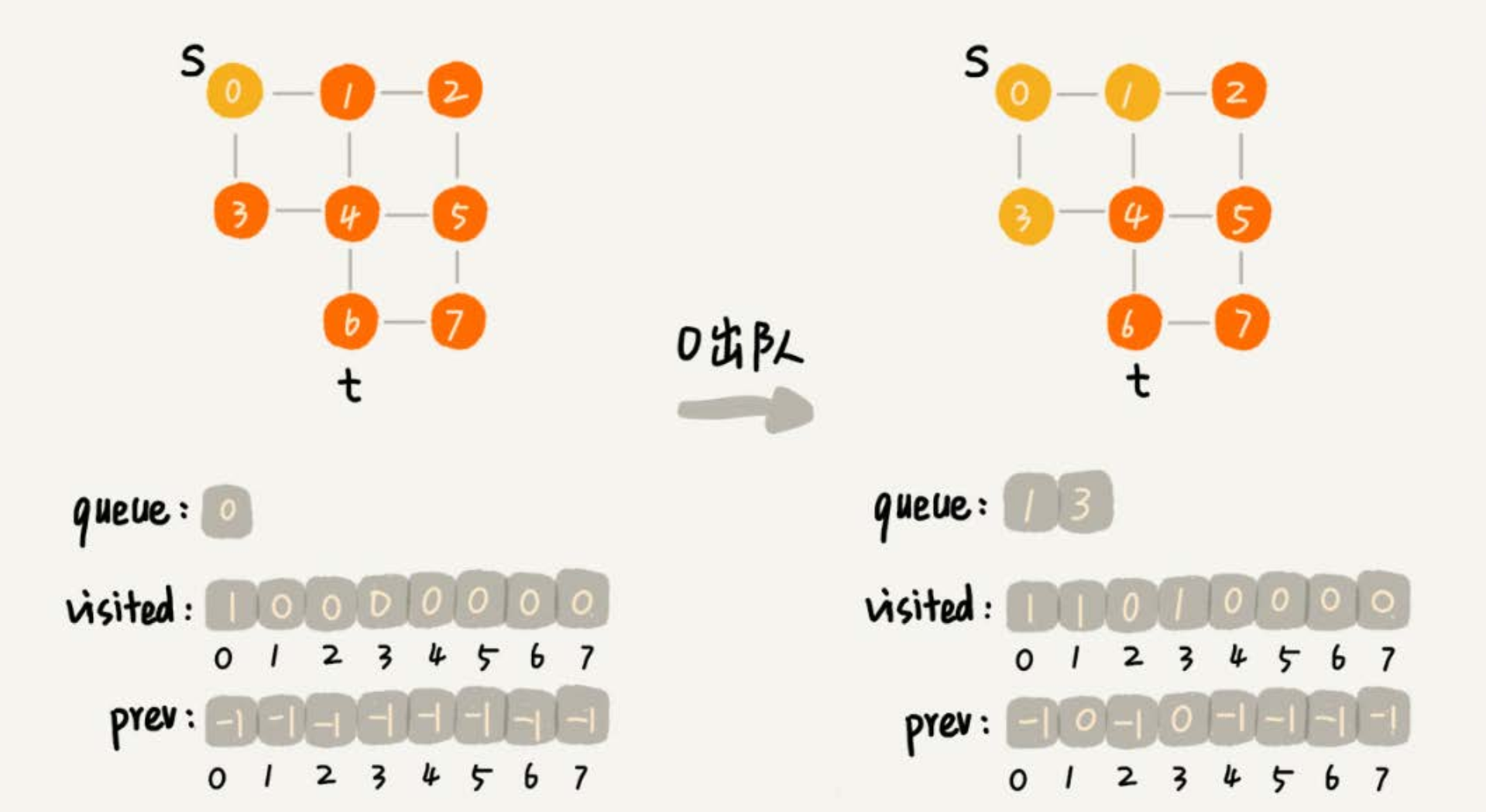
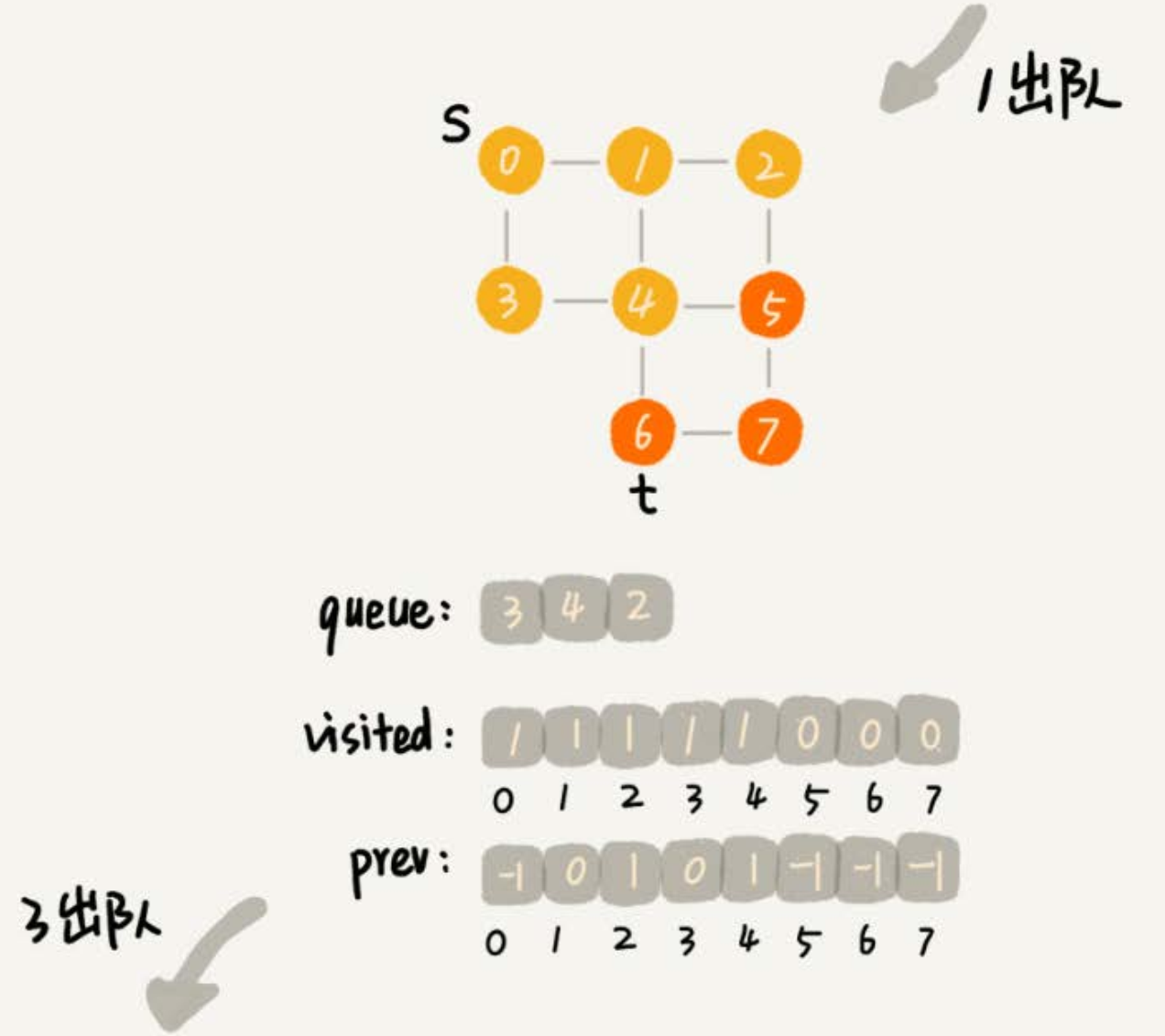
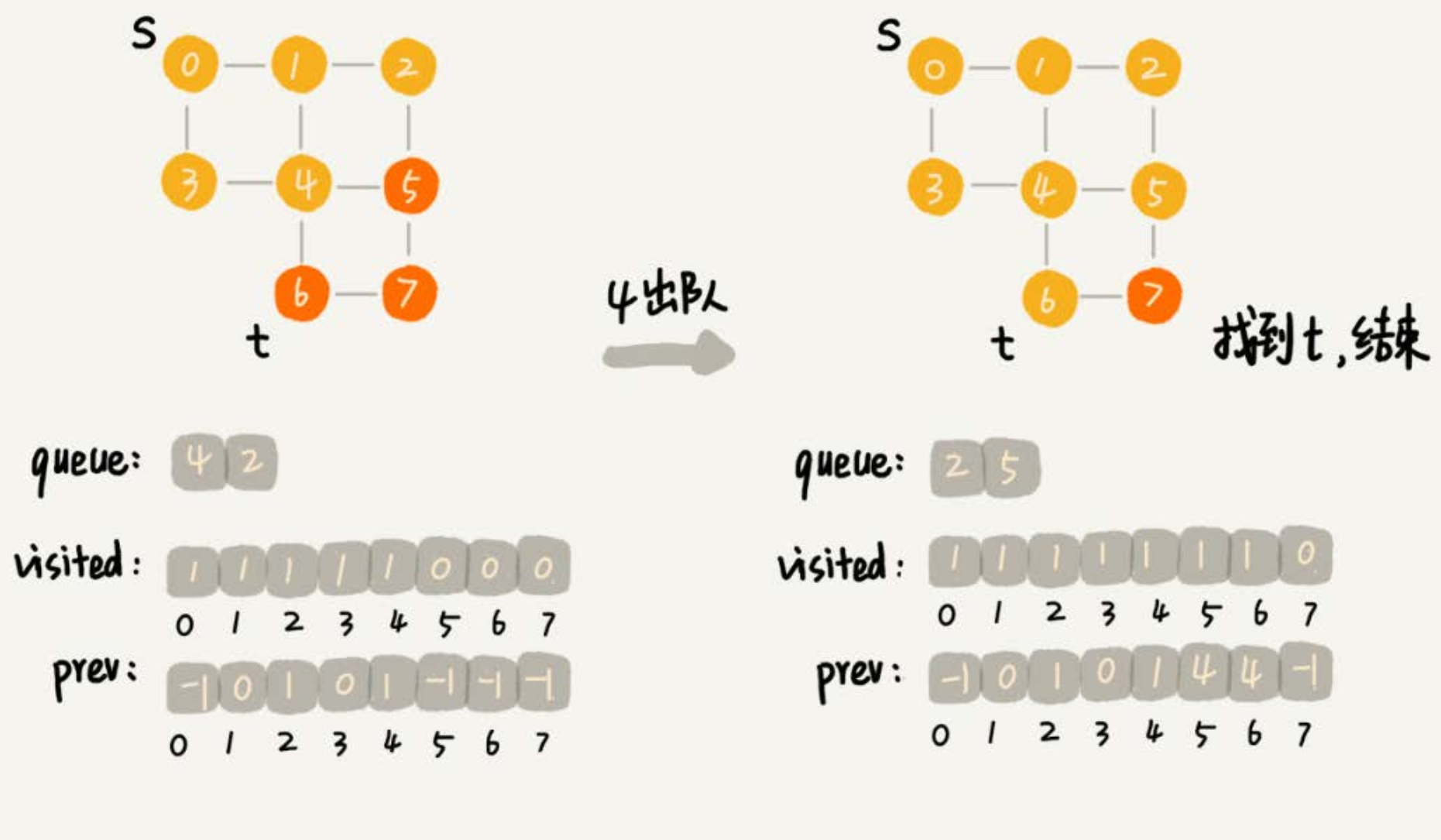
原理如下：

• 
• 
• 

2.2、复杂度分析

• 最坏情况下，终止顶点 t 离起始顶点 s 很远，需要遍历完整个图才能找到。
• 这个时候，每个顶点都要进出一遍队列，每个边也都会被访问一次，所以，广度优先搜索的时间复杂度是 O(V+E)。
• 其中，V 表示顶点的个数，E 表示边的个数。
• 对于一个连通图来说，也就是说一个图中的所有顶点都是连通的，E肯定要大于等于 V-1，所以，广度优先搜索的时间复杂度也可以简写为 O(E)。
• 广度优先搜索的空间消耗主要在几个辅助变量 visited 数组、queue 队列、prev 数组上。
• 这三个存储空间的大小都不会超过顶点的个数，所以空间复杂度是 O(V)。

三、深度优先搜索（DFS）

• 深度优先搜索（Depth-First-Search），简称DFS。
• 最直观的例子就是“走迷宫，假设站在迷宫的某个岔路口，然后想找到出口。
• 随意选择一个岔路口来走，走着走着发现走不通的时候，就回退到上一个岔路口，重新选择一条路继续走，直到最终找到出口。这种走法就是一种深度优先搜索策略。
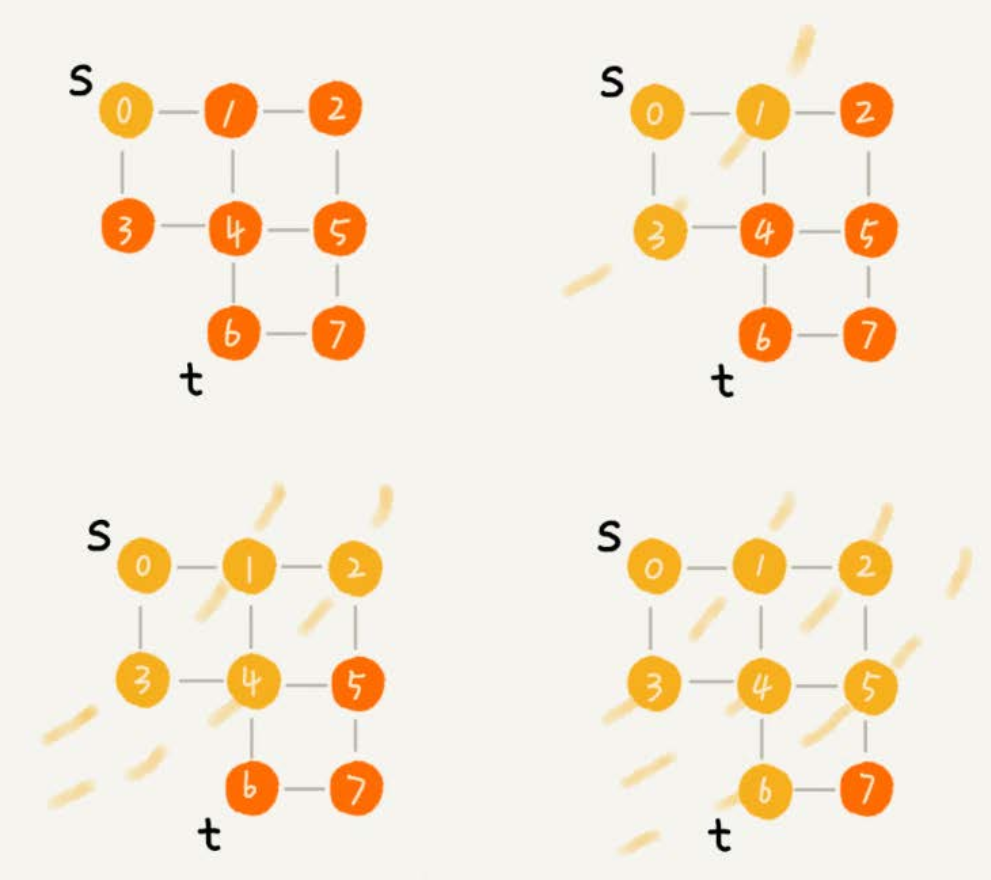
• 如下图所示，在图中应用深度优先搜索，来找某个顶点到另一个顶点的路径。
• 搜索的起始顶点是 s，终止顶点是 t，在图中寻找一条从顶点 s 到顶点 t 的路径。
• 用深度递归算法，把整个搜索的路径标记出来了。实线箭头表示遍历，虚线箭头表示回退。
• 从图中可以看出，深度优先搜索找出来的路径，并不是顶点 s 到顶点 t 的最短路径。
• 

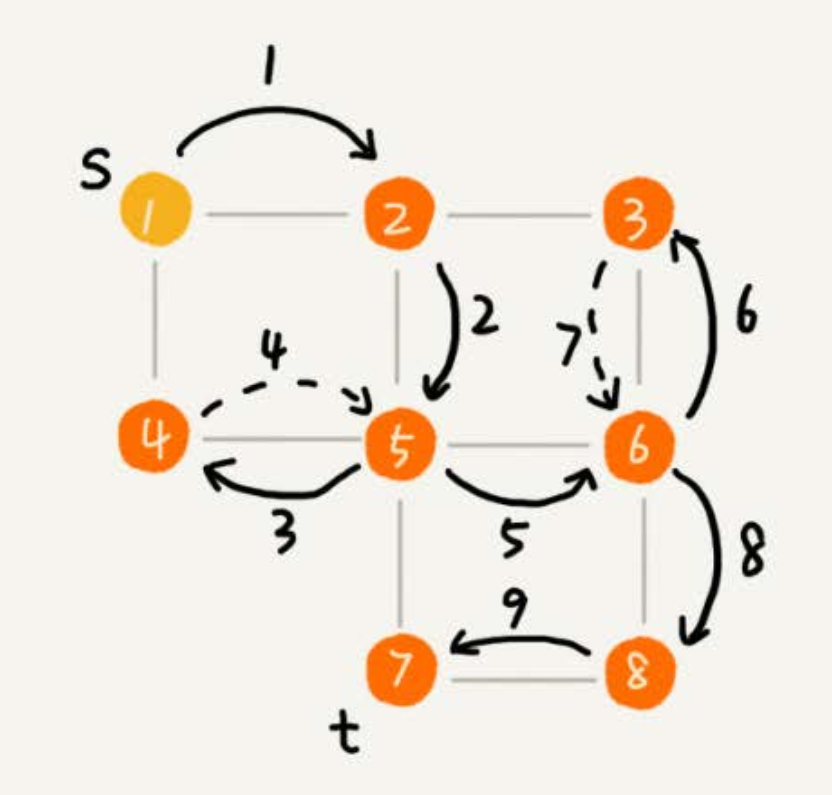
3.1、实现过程

// 全局变量或者类成员变量，标记是否找到终点 t
boolean found = false;

/**
 * 深度优先搜索
 *
 * @param s 起始顶点
 * @param t 终止顶点
 */
public void dfs(int s, int t) {
    found = false;
    // 标记顶点是否被访问
    boolean[] visited = new boolean[v];
    // prev 用来记录搜索路径，prev[w] = a 表示 w 顶点的上一级节点为 a
    int[] prev = Arrays.stream(new int[v])
            .map(f -> -1).toArray();

    recurDfs(s, t, visited, prev);
    print(prev, s, t);
}

private void recurDfs(int w, int t, boolean[] visited, int[] prev) {
    if (found == true) {
        return;
    }
    visited[w] = true;
    if (w == t) {
        found = true;
        return;
    }
    LinkedList<Integer> wLinked = adj[w];
    for (int i = 0; i < wLinked.size(); ++i) {
        int q = wLinked.get(i);
        if (!visited[q]) {
            prev[q] = w;
            recurDfs(q, t, visited, prev);
        }
    }
}

3.2、复杂度分析

• 深度搜索中每条边最多会被访问两次，一次是遍历，一次是回退。
• 所以，深度优先搜索算法的时间复杂度是 O(E)， E 表示边的个数。
• 深度优先搜索算法的消耗内存主要是 visited、 prev 数组和递归调用栈。
• visited、 prev 数组的大小跟顶点的个数V成正比，递归调用栈的最大深度不会超过顶点的个数，所以总的空间复杂度就是 O(V)。

四，两者对比

• 广度优先搜索和深度优先搜索是图上的两种最常用、最基本的搜索算法，比起其他高级的搜索算法，比如A、 IDA等，要简单粗暴，没有什么优化，所以，也被
  
  叫作暴力搜索算法。
• 所以，这两种搜索算法仅适用于状态空间不大，也就是说图不大的搜索。
• 广度优先搜索，通俗的理解就是，地毯式层层推进，从起始顶点开始，依次往外遍历。
• 广度优先搜索需要借助队列来实现，遍历得到的路径就是，起始顶点到终止顶点的最短路径。
• 深度优先搜索用的是回溯思想，非常适合用递归实现。换种说法，深度优先搜索是借助栈来实现的。
• 在执行效率方面，深度优先和广度优先搜索的时间复杂度都是 O(E)，空间复杂度是 O(V)。