2017-2018 ACM-ICPC Northern Eurasia (Northeastern European Regional) Contest (NEERC 17)

2017-2018 ACM-ICPC Northern Eurasia (Northeastern European Regional) Contest (NEERC 17)

A

题意：有 n 个时刻，第 i 个时刻要么会在 (xi,yi) 生成一个半径为 yi 的圆，要么射击 (xi,yi) 这个点，如果该点在某个圆内则把对应圆删除并输出该圆的标号，否则输出 -1 。任意时刻圆之间不会相交（可以相切）。 \(n \le 2*10^5, -10^9 \le x_i,y_i \le 10^9, y_i > 0\)

key：线段树，结论

结论：与一条竖线相交的圆的个数不超过 \(O(\log \max y_i)\) 个。

证明：可以证明下图中，两圆的半径比是 4。也就是说最差时半径以4倍增长。

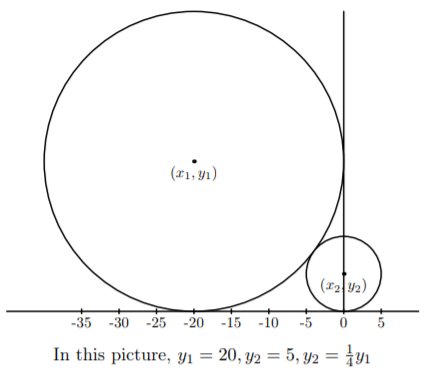
所以每次只需要找到覆盖该竖线的所有圆，然后一个个check即可。可以用线段树维护。

当一个圆插入时，它覆盖的区间最大为 \((x_i-y_i,x_i+y_i)\) 。以查找直线左边的圆为例，只要在 \(x_i\) 处把 \(x_i+y_i\) 插入，之后询问时递归直线左半边，如果区间最大值比 \(x_i\) 小则直接 return。递归到叶子时计算是否可行。

因为至多递归到 log 个叶子，所以总复杂度是 \(O(n\log n \log \max y_i)\)

仔细观察可以发现实际上只有 i+k*m 这个集合中的点有边，并且形成了一个环，而环的大小就是集合中 1 的个数。

I

题意：一个随机排列，偶数按顺序放到 e 数组中，奇数按顺序放到 o 数组中。每次可以询问 \(e_i\) 和 \(o_j\) 的大小关系。求在 \(3*10^5\) 的询问数下输出 e 和 o 。 \(n \le 10000\)

key：排序，交互

考虑快排：每次把区间分为两段。

枚举 o 中的每个数，此时考虑有若干段区间，该数一定存在在某个区间中间（或者是 1 或 n，这个要特判）。由于区间之间存在有序性，所以可以先对所有区间二分，此时该数只会落在两个区间内，然后再从两个区间里暴力判断。由于是随机排列，所以可以证明总询问数是 \(O(n \log n)\)

L

题意：给出树上 m 条路径，询问是否有两条路径相交（包含不算）。 \(n,m \le 2*10^5\)

key：树剖，随机权值

考虑路径覆盖。相离好说，现在问题是如何把相交和包含区分出来。

考虑相交：即做路径覆盖时，被覆盖的每一个点的覆盖状态一致（都没被覆盖/都被某些路径覆盖），否则就一定存在相交。

为了在每个点上保存“被覆盖的状态”，容易想到哈希。实际上只要给每个路径附一个随机的权值，那样可以认为在做的过程中它们任意两个集合的权值异或和不相同（虽然所有集合的异或和肯定有相同的，但是算法执行过程中不会遍历太多的集合）。此时覆盖一条路径时只需要每个点异或上该路径的权值即可。