sklearn中调用PCA算法
sklearn中调用PCA算法
PCA算法是一种数据降维的方法,它可以对于数据进行维度降低,实现提高数据计算和训练的效率,而不丢失数据的重要信息,其sklearn中调用PCA算法的具体操作和代码如下所示:
#sklearn中调用PCA函数进行相关的训练和计算(自定义数据)
import numpy as np
import matplotlib.pyplot as plt
x=np.empty((100,2))
x[:,0]=np.random.uniform(0.0,100.0,size=100)
x[:,1]=0.75*x[:,0]+3.0*np.random.normal(0,3,size=100)
plt.figure()
plt.scatter(x[:,0],x[:,1])
plt.show()
from sklearn.decomposition import PCA #在sklearn中调用PCA机器学习算法
pca=PCA(n_components=1) #定义所需要分析主成分的个数n
pca.fit(x) #对基础数据集进行相关的计算,求取相应的主成分
print(pca.components_) #输出相应的n个主成分的单位向量方向
x_reduction=pca.transform(x) #进行数据的降维
x_restore=pca.inverse_transform(x_reduction) #对降维数据进行相关的恢复工作
plt.figure()
plt.scatter(x[:,0],x[:,1],color="g")
plt.scatter(x_restore[:,0],x_restore[:,1],color="r")
plt.show() #sklearn中利用手写字体的数据集进行实际的PCA算法
#1-1导入相应的库函数
from sklearn import datasets
d=datasets.load_digits()
x=d.data
y=d.target
from sklearn.model_selection import train_test_split
x_train,x_test,y_train,y_test=train_test_split(x,y,random_state=666)
print(x_train.shape)
from sklearn.neighbors import KNeighborsClassifier
knn=KNeighborsClassifier()
knn.fit(x_train,y_train)
print(knn.score(x_test,y_test)) #1-2对于64维的原始数据进行降维,降到2维数据
pca1=PCA(n_components=2)
pca1.fit(x_train)
x_train_re=pca1.transform(x_train) #对于训练数据和测试数据进行降维到二维数据
x_test_re=pca1.transform(x_test)
knn1=KNeighborsClassifier()
knn1.fit(x_train_re,y_train) #再对降维到的二维数据进行KNN算法的训练和测试准确度
print(knn1.score(x_test_re,y_test))
print(pca1.explained_variance_ratio_) #1-3-1对于训练数据和测试数据进行降维到64维数据,维度不变
pca2=PCA(n_components=64) #对于训练数据和测试数据进行降维到64维数据,维度不变
pca2.fit(x_train)
x_train_re=pca2.transform(x_train)
x_test_re=pca2.transform(x_test)
knn1=KNeighborsClassifier()
knn1.fit(x_train_re,y_train)
print(knn1.score(x_test_re,y_test))
print(pca2.explained_variance_ratio_) #输出各个主成分对于整体数据的方差的体现比例
#1-3-2输出前n个主成分所能够反映的数据的特征权重
plt.figure()
plt.plot([i for i in range(x.shape[1])],[np.sum(pca2.explained_variance_ratio_[:i+1]) for i in range(x.shape[1])])
plt.show()
#1-4PCA(a)括号里面的a为0-1的数字,表示输出满足能够反映原始数据比重为a时的最低维度时的PCA,之后进行训练和分类会提高计算的效率5-10倍,但是分类准确度基本相差无几,可以用准确度来换取计算的效率
pca3=PCA(0.95)
pca3.fit(x_train)
print(pca3.n_components_) #输出此时降到的数据维度
x_train_re1=pca3.transform(x_train)
x_test_re1=pca3.transform(x_test)
knn2=KNeighborsClassifier()
knn2.fit(x_train_re1,y_train)
print(knn2.score(x_test_re1,y_test))
#1-5对于64维度数据进行降维到二维数据,之后进行数据的可视化,可以对于不同的分类结果进行查询和可视化区分
pca1=PCA(n_components=2)
pca1.fit(x)
x_re=pca1.transform(x)
plt.figure()
for i in range(10):
plt.scatter(x_re[y==i,0],x_re[y==i,1])
plt.show() 输出结果如下所示:
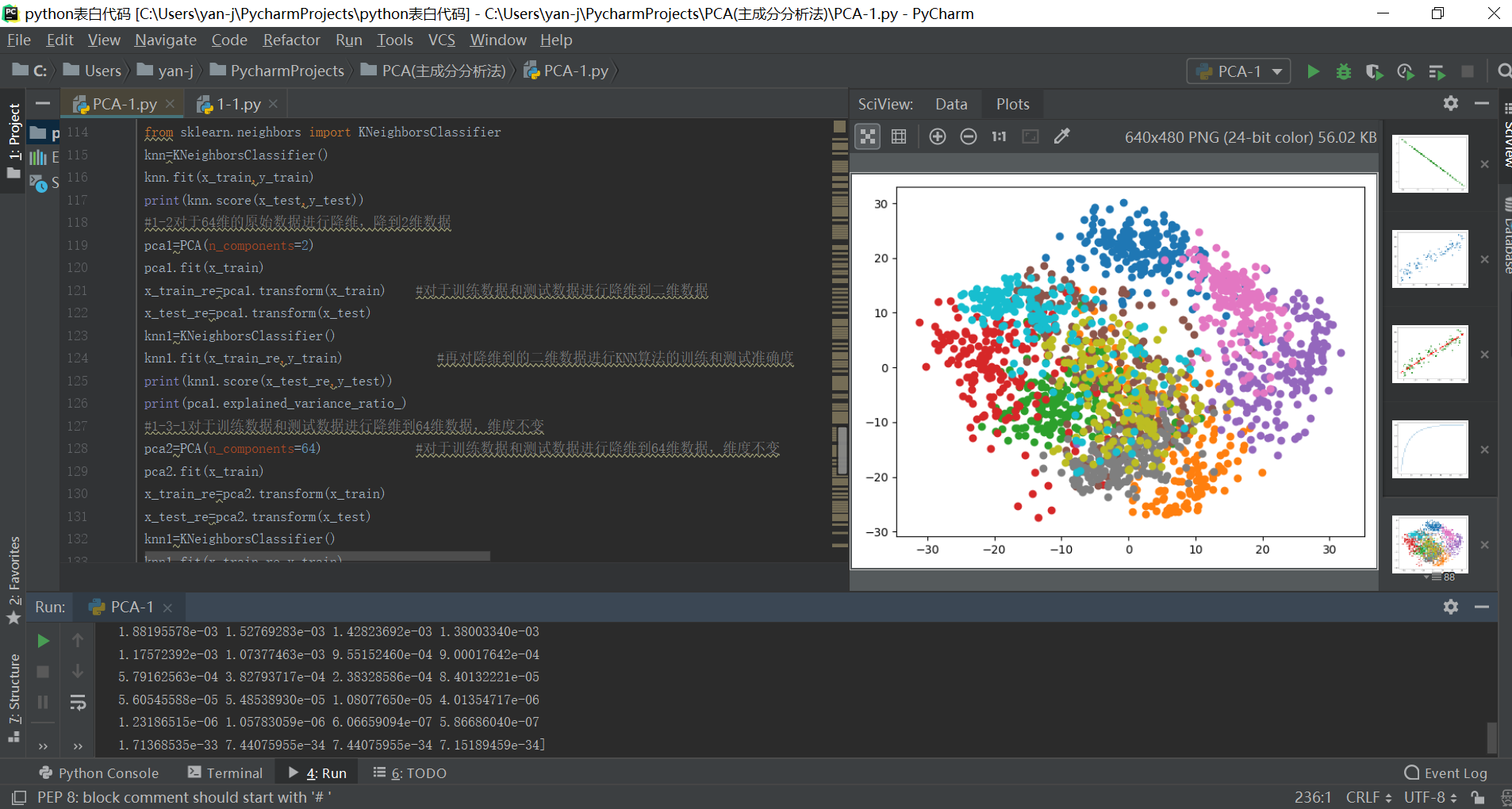
sklearn中调用PCA算法的更多相关文章
- 机器学习实战基础(二十):sklearn中的降维算法PCA和SVD(一) 之 概述
概述 1 从什么叫“维度”说开来 我们不断提到一些语言,比如说:随机森林是通过随机抽取特征来建树,以避免高维计算:再比如说,sklearn中导入特征矩阵,必须是至少二维:上周我们讲解特征工程,还特地提 ...
- sklearn中的多项式回归算法
sklearn中的多项式回归算法 1.多项式回归法多项式回归的思路和线性回归的思路以及优化算法是一致的,它是在线性回归的基础上在原来的数据集维度特征上增加一些另外的多项式特征,使得原始数据集的维度增加 ...
- 机器学习实战基础(二十三):sklearn中的降维算法PCA和SVD(四) PCA与SVD 之 PCA中的SVD
PCA中的SVD 1 PCA中的SVD哪里来? 细心的小伙伴可能注意到了,svd_solver是奇异值分解器的意思,为什么PCA算法下面会有有关奇异值分解的参数?不是两种算法么?我们之前曾经提到过,P ...
- sklearn中调用集成学习算法
1.集成学习是指对于同一个基础数据集使用不同的机器学习算法进行训练,最后结合不同的算法给出的意见进行决策,这个方法兼顾了许多算法的"意见",比较全面,因此在机器学习领域也使用地非常 ...
- 机器学习实战基础(二十四):sklearn中的降维算法PCA和SVD(五) PCA与SVD 之 重要接口inverse_transform
重要接口inverse_transform 在上周的特征工程课中,我们学到了神奇的接口inverse_transform,可以将我们归一化,标准化,甚至做过哑变量的特征矩阵还原回原始数据中的特征矩阵 ...
- 机器学习实战基础(二十二):sklearn中的降维算法PCA和SVD(三) PCA与SVD 之 重要参数n_components
重要参数n_components n_components是我们降维后需要的维度,即降维后需要保留的特征数量,降维流程中第二步里需要确认的k值,一般输入[0, min(X.shape)]范围中的整数. ...
- 机器学习实战基础(二十一):sklearn中的降维算法PCA和SVD(二) PCA与SVD 之 降维究竟是怎样实现
简述 在降维过程中,我们会减少特征的数量,这意味着删除数据,数据量变少则表示模型可以获取的信息会变少,模型的表现可能会因此受影响.同时,在高维数据中,必然有一些特征是不带有有效的信息的(比如噪音),或 ...
- 机器学习实战基础(二十七):sklearn中的降维算法PCA和SVD(八)PCA对手写数字数据集的降维
PCA对手写数字数据集的降维 1. 导入需要的模块和库 from sklearn.decomposition import PCA from sklearn.ensemble import Rando ...
- sklearn中的KMeans算法
1.聚类算法又叫做“无监督分类”,其目的是将数据划分成有意义或有用的组(或簇).这种划分可以基于我们的业务需求或建模需求来完成,也可以单纯地帮助我们探索数据的自然结构和分布. 2.KMeans算法将一 ...
随机推荐
- 温湿度传感器AM2302(DH22)
AM2302 3.3V - 5.5V,建议供电电压为 5V单总线通信模式时,SDA 上拉(开漏)后与微处理器的 I/O 端口相连.单总线通信特殊说明: 0.功耗待机40~50uA;测量1~1.5m ...
- SqlServer游标操作
CLOSE orderNum_02_cursordeallocate orderNum_02_cursorDECLARE orderNum_02_cursor cursor SCROLL for se ...
- Python基础入门语法1
PY的交换值的方法 x.y = y.x PY既具有动态脚本的特性,又有面向对象的特性 PY的缺点: 编译型的语言(C++,C):通过编译器进行编译成机器码,越接近底层,开发效率低 解释型代码:PY和J ...
- SpringMVC 配置文件详解
HandlerMapping 处理器映射 HTTP请求被DispatcherServlet拦截后,会调用HandlerMapping来处理,HandlerMapping根据 url<=&g ...
- MyBatis 入门Demo
新建数据库my_db,新建表student_tb id为主键,不自动递增. 不必插入数据. 下载MyBatis https://github.com/mybatis/mybatis-3/release ...
- GO 空白标识符 _
空白标识符 _ 也被用于抛弃值,如值 5 在:_, b = 5, 7 中被抛弃. _ 实际上是一个只写变量,你不能得到它的值.这样做是因为 Go 语言中你必须使用所有被声明的变量,但有时你并不需要使用 ...
- win7系统中开启wifi热点
1.进入cmd下 2.输入命令创建一个热点,名称为testwifi,密码为12345678 netsh wlan 3.进入网络和共享中心->更改适配器设置,看到多出一个“无线网络连接2”,选中本 ...
- RESTFul Client入门实例
client.html文件内容为: <!DOCTYPE html> <html> <head> <title>RESTFul Client test p ...
- 实用类-<Math类常用>
Math.random() //取0~1之间的随机数(不包括1) Math.max(数字1,数字2) //取两个数中最大的一个 Math.min(数字1,数字2) //取两个数中最小的一个 Math. ...
- Day1-B-CF-1144B
简述:有一个n个元素的序列,选奇数下一个就选偶数,偶数则下一个就是奇数,问能否取完,能取完输出0,否则输出能剩下的最小的之和 思路:统计奇偶数个数,若相等或相差一则取完,否则排列后取出最小的前x个(x ...
