hdoj 1950 Bridging signals【二分求最大上升子序列长度】【LIS】

Bridging signals

Time Limit: 5000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 961    Accepted Submission(s):
627

Problem Description

'Oh no, they've done it again', cries the chief
designer at the Waferland chip factory. Once more the routing designers have
screwed up completely, making the signals on the chip connecting the ports of
two functional blocks cross each other all over the place. At this late stage of
the process, it is too
expensive to redo the routing. Instead, the engineers
have to bridge the signals, using the third dimension, so that no two signals
cross. However, bridging is a complicated operation, and thus it is desirable to
bridge as few signals as possible. The call for a computer program that finds
the maximum number of signals which may be connected on the silicon surface
without rossing each other, is imminent. Bearing in mind that there may be
housands of signal ports at the boundary of a functional block, the problem asks
quite a lot of the programmer. Are you up to the task?

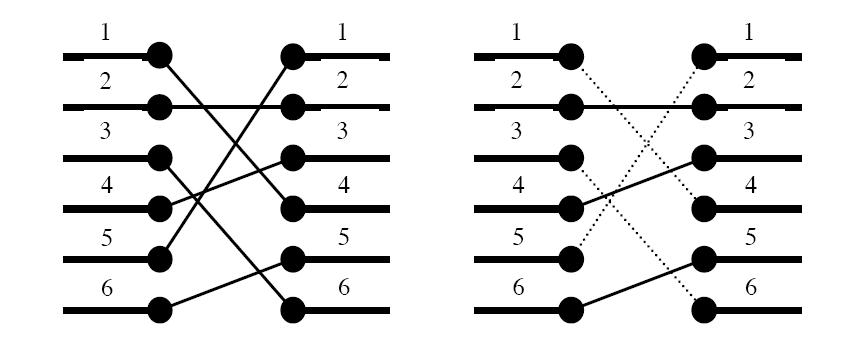
Figure 1. To the left: The two blocks' ports
and their signal mapping (4,2,6,3,1,5). To the right: At most three signals may
be routed on the silicon surface without crossing each other. The dashed signals
must be bridged.

A typical situation is schematically depicted in figure
1. The ports of the two functional blocks are numbered from 1 to p, from top to
bottom. The signal mapping is described by a permutation of the numbers 1 to p
in the form of a list of p unique numbers in the range 1 to p, in which the i:th
number pecifies which port on the right side should be connected to the i:th
port on the left side.
Two signals cross if and only if the straight lines
connecting the two ports of each pair do.

 

Input

On the first line of the input, there is a single
positive integer n, telling the number of test scenarios to follow. Each test
scenario begins with a line containing a single positive integer p<40000, the
number of ports on the two functional blocks. Then follow p lines, describing
the signal mapping: On the i:th line is the port number of the block on the
right side which should be connected to the i:th port of the block on the left
side.

 

Output

For each test scenario, output one line containing the
maximum number of signals which may be routed on the silicon surface without
crossing each other.

 

Sample Input

4

6

4

2

6

3

1

5

 

10

2

3

4

5

6

7

8

9

10

1

 

 

8

8

7

6

5

4

3

2

1

 

9

5

8

9

2

3

1

7

4

6

 

Sample Output

3

9

1

4

题意：从左侧的图中去掉一些线段使剩余的线段都不相交，问最多能够剩下多少条线段

题解：由观察可知要想剩下的线段都不相交，则要求右侧线为单调递增的排序因为数据很大为避免超时

        用二分法求最大递增序列的长度

求最大子序列长度的原理：

      用一组数据来说明：5 8 9 2 3 1 7 4 6

显然我们可以观察出最长的子序列是2 3 4 6长度为四，设出一个数组a[]来存放子序列 设top=1为子序列长度；

接下来我们一个一个遍历  首先是5 则a[top++]=5;然后是8因为8>5所以a[top++]=8；9>8所以a[top++]=9

此时a数组中的元素为5 8 9；接下来遍历到2；因为5在当前a数组中最小而2<5,所以用2来覆盖5此时数组a变为2 8 9

接下来遍历到3因为2<3<8所以用3覆盖8此时数组a变为2 3 9接下来同理1覆盖2；7覆盖9；4覆盖7；到6时因为数组a

中所有数都比6小所以a[top++]=6;此时数组a中元素为1 3 4 6长度为top；（此法只能用来求最大递增子序列的长度

不能打印出最大递增子序列）

AC代码：

#include<stdio.h>
#include<string.h>
int main()
{
	int t;
	int p,top,l,r,mid,i,m;
	int a[44000];
	scanf("%d",&t);
	while(t--)
	{
		scanf("%d",&p);
		scanf("%d",&a[0]);
		int top=0;
		for(i=1;i<p;i++)
		{
			scanf("%d",&m);
			if(a[top]<m)
				a[++top]=m;
			else
			{
				l=0;r=top;mid=0;
			    while(r>=l)
			    {
	    			mid=(r+l)/2;
	    			if(a[mid] < m)
	    			l=mid+1;
	    			else
	    			r=mid-1;
    			}
    			a[r+1]=m;
			}
		}
		printf("%d\n",top+1);
	}
	return 0;
}