卷积网络中的通道(Channel)和特征图

转载自：https://www.jianshu.com/p/bf8749e15566

今天介绍卷积网络中一个很重要的概念，通道（Channel），也有叫特征图（feature map）的。

首先，之前的文章也提到过了，卷积网络中主要有两个操作，一个是卷积(Convolution)，一个是池化(Pooling)。

其中池化层并不会对通道之间的交互有影响，只是在各个通道中进行操作。

而卷积层则可以在通道与通道之间进行交互，之后在下一层生成新的通道，其中最显著的就是Incept-Net里大量用到的1x1卷积操作。基本上完全就是在通道与通道之间进行交互，而不关心同一通道中的交互。

一般大家说通道指的是图片的色彩通道，而特征图是卷积过滤器的输出结果。但实际上，两者本质上是相同的，都是表示之前输入上某个特征分布的数据。

那么先来看看为什么可以说它们是相同的。

 

数码相机中的“卷积”

通道这个概念最初指的是电子图片中RGB通道，或者CMYK通道这样的配色方案，比如说一张RGB的64x64的图片，可以用一个64x64x3的张量来表示。这里的3指的就是通道，分别为红色(Red)、绿色(Green)、蓝色(Blue)三个通道。

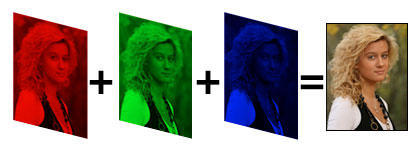
因为这三种颜色是三原色，所以基本上可以合成任何人眼可分辨的颜色。而三个通道的图片也基本上可以表示所有图片了。

在计算机视觉处理中，一般图片数据除了是单通道的灰度图片外，就是RGB通道的彩色图片了。

对RGB图片进行卷积操作后，根据过滤器的数量就可以产生更多的通道。事实上，多数情况还是叫后面的卷积层中的通道为，特征图。但实际上在张量表示下，特征图和前面提到的通道差不多，有时候后面的也都叫通道了。一种卷积核得到一个通道，所以特征图个数=输出通道数=卷积核个数。

通道与特征

这样看来，图片中的通道就是某种意义上的特征图。一个通道是对某个特征的检测，通道中某一处数值的强弱就是对当前特征强弱的反应。

如一个蓝色通道中，如果是256级的话，那么一个像素如果是255的话那么就表示蓝色度很大。从这个角度来看灰度图片的话，就会发现其实灰度图片就是一个白色过滤器生成的特征图。

于是卷积网络中的特征图，也能够很直接地理解为通道了。

之后通过对一定范围的特征图进行卷积，可以将多个特征组合出来的模式抽取成一个特征，获得下一个特征图。之后再继续，对特征图进行卷积，特征之间继续组合，获得更复杂的特征图。

又因为池化层的存在，会不断提取一定范围内最强烈的特征，并且缩小张量的大小，使得大范围内的特征组合也能够捕捉到。

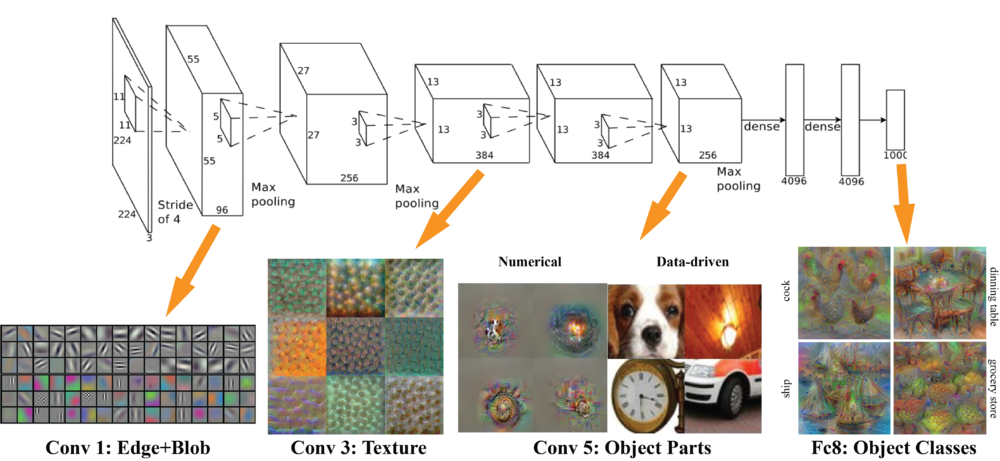
对单个特征图进行视觉化的话，会发现它是在对什么特征进行捕捉。最近一个很有意思的Blog文章就展示了这方面的结果，很有意思。

通过特征角度来看卷积网络的话，那么1x1卷积也就很好理解了。即使1x1卷积前后的张量大小完全不变，比如说16x16x64 -> 16x16x64这样的卷积，看上去好像是没有变化。但实际上，可能通过特征之间的互动，已经由之前的64个特征图组成了新的64个特征图。

有时候我理解一个这样的1x1卷积操作，就会把它当成是一次对之前特征的整理。

通道的终点

这样子不停卷积下去，直到最后一层，剩下一个一维向量时，每个标量代表着一个通道，捕捉到的特征又是什么呢。

如果是物体分类任务的话，就正是我们需要输出判别的一个个物体类别。

比如说第一个数是代表猫特征，第二个数代表狗特征，第三个代表人... 这个时候去从里面选数值最大那个当做分类的种类就好了。

到这里可能仔细的人会注意，最后几层不是没卷积操作吗，而是全连接网络。

一个概念上需要澄清的是，虽然说1x1卷积，而且也从融合特征角度，给了它特殊的理解。但如果再仔细看看的话，就会发现实际上1x1卷积就是全连接网络。所以我们可以把最后的1x1网络当成某种程度上的1x1卷积。

上面的网络最后几层，将张量展平然后输入全连接网络。因为剩下的特征图中都保留了很重要的信息，为了利用所有的信息，并且让它们获得足够的交互，所以直接输入全连接网络，获得最后的特征向量。

这个特征向量能够用来干什么呢。一个很有趣的应用案例是Siamese网络。输入一张脸，输出一个128的特征向量，于是这个向量就类似于ID号码。

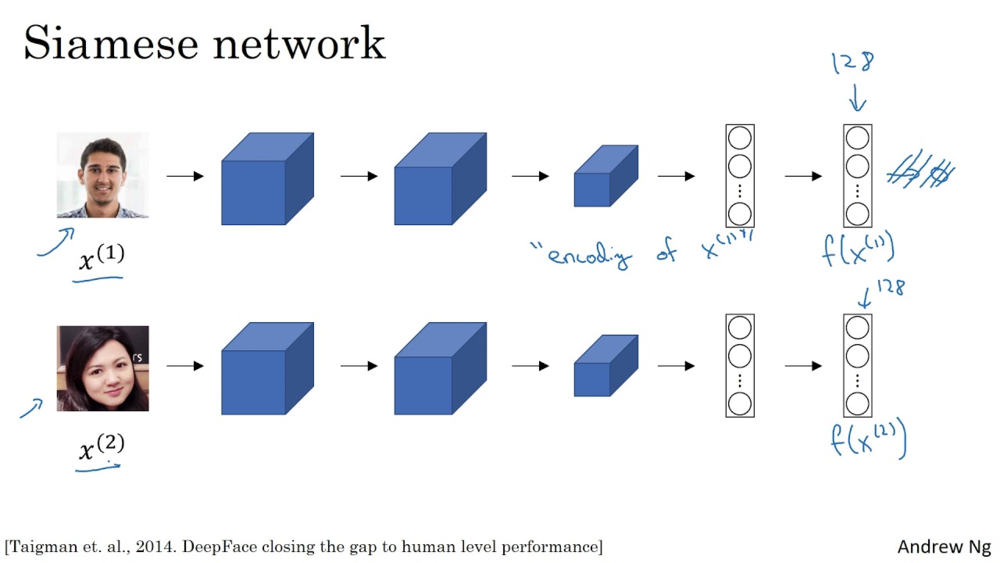
之后再输入一张脸，得到一个特征向量，这时候只需要比较一下获得的两个特征向量就能够知道这两张脸是不是同一个人。

如果将最后的特征向量视觉化，或许我们还能发现，向量中每个标量所代表的特征，比如说眼睛之间的间距，肤色...

用本文的通道来说的话，最后获得了一个128个通道向量表示。