cf446C DZY Loves Fibonacci Numbers

C. DZY Loves Fibonacci Numbers

time limit per test

4 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

In mathematical terms, the sequence Fn of
Fibonacci numbers is defined by the recurrence relation

F1 = 1; F2 = 1; Fn = Fn - 1 + Fn - 2 (n > 2).

DZY loves Fibonacci numbers very much. Today DZY gives you an array consisting of n integers: a1, a2, ..., an.
Moreover, there are mqueries, each query has one of the two types:

1. Format of the query "1 l r". In reply to the query, you need to add Fi - l + 1 to
   each element ai,
   where l ≤ i ≤ r.
2. Format of the query "2 l r". In reply to the query you should output the value of 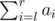 modulo 1000000009 (109 + 9).

Help DZY reply to all the queries.

Input

The first line of the input contains two integers n and m (1 ≤ n, m ≤ 300000).
The second line contains n integers a1, a2, ..., an (1 ≤ ai ≤ 109) —
initial array a.

Then, m lines follow. A single line describes a single query in the format given in the statement. It is guaranteed that for each query inequality 1 ≤ l ≤ r ≤ n holds.

Output

For each query of the second type, print the value of the sum on a single line.

Sample test(s)

input

4 4
1 2 3 4
1 1 4
2 1 4
1 2 4
2 1 3

output

17
12

Note

After the first query, a = [2, 3, 5, 7].

For the second query, sum = 2 + 3 + 5 + 7 = 17.

After the third query, a = [2, 4, 6, 9].

For the fourth query, sum = 2 + 4 + 6 = 12.

题意是给定一个数列，要求支持两种操作：1是在区间[l,r]上的所有数依次加上斐波那契数列的前(r-l+1)项；2是区间求和

显然很容易看出这是线段树。

区间求和是很简单的，关键是线段树节点的标记怎么打

和普通的区间加减的标记不同，加减标记可以直接在左右节点上修改。但是加斐波那契数不行。因为假设当前这一段要加上斐波那契数列[l1 , r1]，它的左儿子的标记是[l2 , r2]。那么下传的时候直接改成[l1+l2 , r1+r2]绝对不行。

所以我们必须考虑怎样转移标记。

突破口应该还是在斐波那契数本身上。由于斐波那契数的性质a[i]=a[i-1]+a[i-2]，我们可以猜想[l , r] = [l-1 , r-1] + [l-2 , r-2]，并很容易证明这是正确的。

不只是这样，对于区间[l , r]，令len=r - l + 1 ，则[l , r]一定可以表示为 t1 * [1 , len] + t2 * [2 , len+1]。因为[l , r] = [l-1 , r-1] + [l-2 , r-2]， [l-1 , r-1] =  [l-2 , r-2] +  [l-3 , r-3]……这样无限递归下去，容易看出只有l != 1且l != 2时存在区间[l-2 , r-2]。那么[l , r]一定可以变为若干[l-1 , r-1]和[l-2 , r-2]的和。当然变化时区间长度len=r-l+1显然是不会变的。所以对于一个节点，我们只要知道一个len=r-l+1，然后无论有多么复杂的斐波那契数的区间加在一起，总可以用t1、t2表示。这样就很好写pushdown了。

然而还有一个问题需要我们解决，那就是求出对于给定的l（只要知道l就可以了。至于为什么请自行脑补），[l , r] = 多少[l-1 , r-1] + 多少[l-2 , r-2]。

假设我们用二元组（t1,t2）可以表示l，那么很容易写出前几项：

1=(1 , 0)……[1 , len]=0 * [2 , len+1] + 1 * [1 , len]

2=(0 , 1)……[2 , len+1]=1 * [2 , len+1] + 0 * [1 , len]

3=(1 , 1)……[3 , len+2]=1 * [2 , len+1] + 1 * [1 , len]

4=(1 , 2)……[4 , len+3]=1 * [2 , len+1] + 2 * [1 , len]

5=(2 , 3)……[5 , len+4]=2 * [2 , len+1] + 3 * [1 , len]

……（发现规律了吧！以下就不列举了）

那么我们直接预处理出对于l的t1、t2，方便调用。最后该怎么搞就怎么搞

(对了在这里说一下，为什么t1、t2在递归的时候也可以取模？因为假设我们求一个区间的和，令s[]表示斐波那契数的前缀和取模，令t1=T1+mod , t2=T2+mod。那么区间和是t1 * s[len] + t2 * (s[len+1]-s[1])，拆开来就是T1 * s[len] + T2 * (s[len+1]-s[1]) + mod * (s[len]+s[len+1]-s[1])，对mod取模之后显然就是T1 * s[len] + T2 * (s[len+1]-s[1])。所以取模之后是一样的)

但是，这样常数好像巨大！所以我第十个点就T了

先贴个代码吧

#include<cstdio>
#define LL long long
#define mod 1000000009
struct trees{
	int l,r,ls,rs;
	long long tot,t1,t2;
}tree[800001];
inline int read()
{
    int x=0,f=1;char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
    return x*f;
}
int n,m,opr,x,y,treesize;
int a[210001];
int F[310001];
int s[310001];
int sF[310001];
int F1[310001];
int F2[310001];
inline void update(int k)
{
	tree[k].tot=tree[tree[k].ls].tot+tree[tree[k].rs].tot;
	while (tree[k].tot>mod) tree[k].tot-=mod;
}
inline void pushdown(int k)
{
	int l=tree[k].l,r=tree[k].r;
	LL t1=tree[k].t1,t2=tree[k].t2;
	tree[k].t1=0;tree[k].t2=0;
	if (r==l)return;
	int len=r-l+1,llen=len-(len>>1),ls=tree[k].ls,rs=tree[k].rs;
	tree[ls].tot+=t1*sF[llen]+t2*(sF[llen+1]-1);
	tree[ls].tot%=mod;
	tree[ls].t1+=t1;
	while (tree[ls].t1>mod) tree[ls].t1-=mod;
	tree[ls].t2+=t2;
	while (tree[ls].t2>mod) tree[ls].t2-=mod;
	tree[rs].tot+=t1*(sF[len]-sF[llen])+t2*(sF[len+1]-sF[llen+1]);
	tree[rs].tot%=mod;
	tree[rs].t1=(tree[rs].t1+t1*F1[llen+1]+t2*F1[llen+2])%mod;
	tree[rs].t2=(tree[rs].t2+t1*F2[llen+1]+t2*F2[llen+2])%mod;
	update(k);
}
inline void buildtree(int l,int r)
{
	if (l>r) return;
	int now=++treesize;
	tree[now].l=l;
	tree[now].r=r;
	if (l==r)return;
	int mid=(l+r)>>1;
	tree[now].ls=treesize+1;
	buildtree(l,mid);
	tree[now].rs=treesize+1;
	buildtree(mid+1,r);
	update(now);
}
inline void change(int now,int x,int y,LL t1,LL t2)
{
	if(tree[now].t1||tree[now].t2)pushdown(now);
	t1%=mod;t2%=mod;
	int l=tree[now].l,r=tree[now].r,len=r-l+1;
	if (x==l&&y==r)
	{
		tree[now].t1=t1;
		tree[now].t2=t2;
		tree[now].tot+=t1*sF[len]+t2*(sF[len+1]-1);
		tree[now].tot%=mod;
		return;
	}
	int mid=(l+r)>>1;
	if (mid>=y)change(tree[now].ls,x,y,t1,t2);
	else if(mid<x)change(tree[now].rs,x,y,t1,t2);
	else
	{
		change(tree[now].ls,x,mid,t1,t2);
		int rest=mid-x+2;
		change(tree[now].rs,mid+1,y,t1*F1[rest]+t2*F1[rest+1],t1*F2[rest]+t2*F2[rest+1]);
	}
	update(now);
}
inline long long ask(int now,int x,int y)
{
	if(tree[now].t1||tree[now].t2)pushdown(now);
	int l=tree[now].l,r=tree[now].r;
	if (l==x&&r==y)return tree[now].tot;
	int mid=(l+r)>>1;
	if (mid>=y)return ask(tree[now].ls,x,y);
	else if (mid<x)return ask(tree[now].rs,x,y);
	else return ask(tree[now].ls,x,mid)+ask(tree[now].rs,mid+1,y);
}
int main()
{
	//freopen("cf.in","r",stdin);
	//freopen("cf.out","w",stdout);
	n=read();m=read();
	F[1]=F[2]=sF[1]=F1[1]=F2[2]=1;sF[2]=2;
	for (int i=3;i<=n+3;++i)
	{
	  F[i]=(F[i-1]+F[i-2])%mod;
	  sF[i]=(sF[i-1]+F[i])%mod;
	  F1[i]=(F1[i-1]+F1[i-2])%mod;
	  F2[i]=(F2[i-1]+F2[i-2])%mod;
	}
	for (int i=1;i<=n;++i)
	{
		a[i]=read();
		s[i]=s[i-1]+a[i];
	}
	buildtree(1,n);
	for (int i=1;i<=m;++i)
	{
		opr=read();x=read();y=read();
		if (opr==1)change(1,x,y,1,0);
		if (opr==2)printf("%lld\n",(ask(1,x,y)%mod+s[y]-s[x-1])%mod);
	}
	return 0;
}

可以看出pushdown是有多长……但是确实有太多东西要处理，而且我已经加了一些常数优化，比如取模的时候改成减法，这样速度快一点点。还有在pushdown之前加一行判断，只有在t1、t2至少有一个不为0的时候才值得标记下传。但这样n=m=30w的数据还是会爆。

最后我去看了一下A的人的代码是如何写的。也不班门弄斧了，附代码：

#include <algorithm>
#include <iostream>
#include <cstring>
#include <string>
#include <cstdio>
#include <vector>
#include <cmath>
#include <queue>
#include <set>
#include <map>
#define lson (2*id)
#define rson (2*id+1)
using namespace std;
const __int64 p=1000000009;
const __int64 q1=691504013,q2=308495997;
const __int64 k=276601605;
int n,Q;
__int64 a[300005],p1[300005],p2[300005];
__int64 sp1[300005],sp2[300005];
struct tree
{
    int l,r,len;
    __int64 s1,s2,first1,first2;
}tr[1200005];
void build(int l,int r,int id)
{
    tr[id].l=l;
    tr[id].r=r;
    tr[id].len=r-l+1;
    tr[id].first2=tr[id].first1=0;
    tr[id].s1=tr[id].s2=0;
    if(l!=r)
    {
        int mid=(tr[id].l+tr[id].r)/2;
        build(l,mid,lson);
        build(mid+1,r,rson);
    }
}
void pushdown(int id)
{
    if(tr[id].first1!=0)
    {
        __int64 t=tr[id].first1;
        tr[id].first1=0;
        tr[lson].s1=(tr[lson].s1+t*sp1[tr[lson].len-1])%p;
        tr[lson].first1=(tr[lson].first1+t)%p;
        tr[rson].s1=(tr[rson].s1+t*p1[tr[lson].len]%p*sp1[tr[rson].len-1])%p;
        tr[rson].first1=(tr[rson].first1+t*p1[tr[lson].len])%p;
    }
    if(tr[id].first2!=0)
    {
        __int64 t=tr[id].first2;
        tr[id].first2=0;
        tr[lson].s2=(tr[lson].s2+t*sp2[tr[lson].len-1])%p;
        tr[lson].first2=(tr[lson].first2+t)%p;
        tr[rson].s2=(tr[rson].s2+t*p2[tr[lson].len]%p*sp2[tr[rson].len-1])%p;
        tr[rson].first2=(tr[rson].first2+t*p2[tr[lson].len])%p;
    }
}
void update(int l,int r,int id,int x)
{
    if(tr[id].l>=l&&tr[id].r<=r)
    {
        int y=tr[id].l-l+x;
        tr[id].s1=(tr[id].s1+k*p1[y]%p*sp1[tr[id].len-1]%p)%p;
        tr[id].s2=(tr[id].s2+k*p2[y]%p*sp2[tr[id].len-1]%p)%p;
        tr[id].first1=(tr[id].first1+k*p1[y])%p;
        tr[id].first2=(tr[id].first2+k*p2[y])%p;
        return ;
    }
    pushdown(id);
    int mid=(tr[id].l+tr[id].r)/2;
    if(l<=mid) update(l,r,lson,x);
    if(r>mid) update(l,r,rson,x);
    tr[id].s1=(tr[lson].s1+tr[rson].s1)%p;
    tr[id].s2=(tr[lson].s2+tr[rson].s2)%p;
}
__int64 query(int l,int r,int id)
{
    if(tr[id].l>=l&&tr[id].r<=r) return ((tr[id].s1-tr[id].s2)+p)%p;
    pushdown(id);
    int mid=(tr[id].l+tr[id].r)/2;
    __int64 ans1=0,ans2=0;
    if(l<=mid) ans1=query(l,r,lson);
    if(r>mid) ans2=query(l,r,rson);
    return (ans1+ans2)%p;
}
void init()
{
    p1[0]=p2[0]=1;
    sp1[0]=sp2[0]=1;
    scanf("%d%d",&n,&Q);
    for(int i=1;i<=n;i++)
    {
        p1[i]=p1[i-1]*q1%p;
        p2[i]=p2[i-1]*q2%p;
        sp1[i]=(sp1[i-1]+p1[i])%p;
        sp2[i]=(sp2[i-1]+p2[i])%p;
    }
}
int main()
{
    init();
    a[0]=0;
    for(int i=1;i<=n;i++)
    {
        scanf("%I64d",&a[i]);
        a[i]+=a[i-1];
    }
    build(1,n,1);
    while(Q--)
    {
        int op,l,r;
        scanf("%d%d%d",&op,&l,&r);
        if(op==1) update(l,r,1,1);
        else
        {
            __int64 v1=query(l,r,1),v2=((a[r]-a[l-1])+p)%p;
            printf("%I64d\n",(v1+v2)%p);
        }
    }
    return 0;
}

好不容易找到一个像样的线段树……

从代码中发现他的一个显而易见的一个优化：因为是不断加数字进去，所以直接用线段树维护加入的数，而原来的数直接用前缀和处理询问。

但是我看了很久也没看懂前面定义的大常数是什么意思……

如果哪位神犇一眼看出了这有什么用，请不要“不屑于”回答……