神经网络入门篇：详解计算一个神经网络的输出（Computing a Neural Network's output）

一个神经网络的输出

首先，回顾下只有一个隐藏层的简单两层神经网络结构：

图1.3.1

其中，\(x\)表示输入特征，\(a\)表示每个神经元的输出，\(W\)表示特征的权重，上标表示神经网络的层数（隐藏层为1），下标表示该层的第几个神经元。这是神经网络的符号惯例，下同。

神经网络的计算

关于神经网络是怎么计算的，从之前提及的逻辑回归开始，如下图所示。用圆圈表示神经网络的计算单元，逻辑回归的计算有两个步骤，首先按步骤计算出\(z\)，然后在第二步中以sigmoid函数为激活函数计算\(z\)（得出\(a\)），一个神经网络只是这样子做了好多次重复计算。

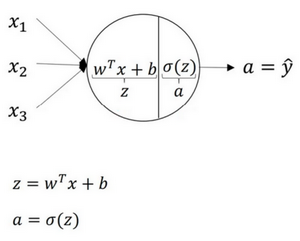
图1.3.2

回到两层的神经网络，从隐藏层的第一个神经元开始计算，如上图第一个最上面的箭头所指。从上图可以看出，输入与逻辑回归相似，这个神经元的计算与逻辑回归一样分为两步，小圆圈代表了计算的两个步骤。

第一步，计算\(z^{[1]}_1,z^{[1]}_1 = w^{[1]T}_1x + b^{[1]}_1\)。

第二步，通过激活函数计算\(a^{[1]}_1,a^{[1]}_1 = \sigma(z^{[1]}_1)\)。

隐藏层的第二个以及后面两个神经元的计算过程一样，只是注意符号表示不同，最终分别得到\(a^{[1]}_2、a^{[1]}_3、a^{[1]}_4\)，详细结果见下:

\(z^{[1]}_1 = w^{[1]T}_1x + b^{[1]}_1, a^{[1]}_1 = \sigma(z^{[1]}_1)\)

\(z^{[1]}_2 = w^{[1]T}_2x + b^{[1]}_2, a^{[1]}_2 = \sigma(z^{[1]}_2)\)

\(z^{[1]}_3 = w^{[1]T}_3x + b^{[1]}_3, a^{[1]}_3 = \sigma(z^{[1]}_3)\)

\(z^{[1]}_4 = w^{[1]T}_4x + b^{[1]}_4, a^{[1]}_4 = \sigma(z^{[1]}_4)\)

向量化计算

如果执行神经网络的程序，用for循环来做这些看起来真的很低效。所以接下来要做的就是把这四个等式向量化。向量化的过程是将神经网络中的一层神经元参数纵向堆积起来，例如隐藏层中的\(w\)纵向堆积起来变成一个\((4,3)\)的矩阵，用符号\(W^{[1]}\)表示。另一个看待这个的方法是有四个逻辑回归单元，且每一个逻辑回归单元都有相对应的参数——向量\(w\)，把这四个向量堆积在一起，会得出这4×3的矩阵。

因此，

公式1.8：

\(z^{[n]} = w^{[n]}x + b^{[n]}\)

公式1.9：

\(a^{[n]}=\sigma(z^{[n]})\)

详细过程见下:

公式1.10：

\[a^{[1]} =
\left[
\begin{array}{c}
a^{[1]}_{1}\\
a^{[1]}_{2}\\
a^{[1]}_{3}\\
a^{[1]}_{4}
\end{array}
\right]
= \sigma(z^{[1]})
\]

公式1.11：

\[\left[
\begin{array}{c}
z^{[1]}_{1}\\
z^{[1]}_{2}\\
z^{[1]}_{3}\\
z^{[1]}_{4}\\
\end{array}
\right]
=
\overbrace{
\left[
\begin{array}{c}
...W^{[1]T}_{1}...\\
...W^{[1]T}_{2}...\\
...W^{[1]T}_{3}...\\
...W^{[1]T}_{4}...
\end{array}
\right]
}^{W^{[1]}}
*
\overbrace{
\left[
\begin{array}{c}
x_1\\
x_2\\
x_3\\
\end{array}
\right]
}^{input}
+
\overbrace{
\left[
\begin{array}{c}
b^{[1]}_1\\
b^{[1]}_2\\
b^{[1]}_3\\
b^{[1]}_4\\
\end{array}
\right]
}^{b^{[1]}}
\]

对于神经网络的第一层，给予一个输入\(x\)，得到\(a^{[1]}\)，\(x\)可以表示为\(a^{[0]}\)。通过相似的衍生会发现，后一层的表示同样可以写成类似的形式，得到\(a^{[2]}\)，\(\hat{y} = a^{[2]}\)，具体过程见公式1.8、1.9。

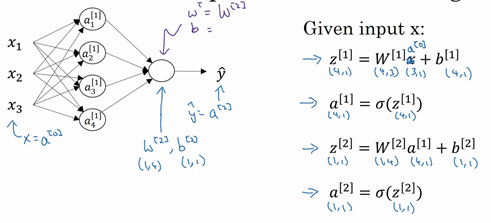
图1.3.3

如上图左半部分所示为神经网络，把网络左边部分盖住先忽略，那么最后的输出单元就相当于一个逻辑回归的计算单元。当有一个包含一层隐藏层的神经网络，需要去实现以计算得到输出的是右边的四个等式，并且可以看成是一个向量化的计算过程，计算出隐藏层的四个逻辑回归单元和整个隐藏层的输出结果，如果编程实现需要的也只是这四行代码。

总结

通过本篇博客，读者应该可以能够根据给出的一个单独的输入特征向量，运用四行代码计算出一个简单神经网络的输出。接下来将了解的是如何一次能够计算出不止一个样本的神经网络输出，而是能一次性计算整个训练集的输出。