【转载】 softmax_cross_entropy_with_logits中“logits”是个什么意思？

原文地址：

https://zhuanlan.zhihu.com/p/51431626

-------------------------------------------------------------

------------------------------------------------------------------

tf.nn.softmax_cross_entropy_with_logits  函数是TensorFlow中常用的求交叉熵的函数。其中函数名中的“logits”是个什么意思呢？它时不时地困惑初学者，下面我们就讨论一下。

1. 什么是logits？

要弄明白Logits，首先要弄明白什么是Odds？

在英文中，Odds的本意是几率、可能性。它和我们常说的概率又有什么区别呢？

在统计学里，概率（Probability）描述的是某事件A出现的次数与所有事件出现的次数之比:

很显然，概率 P是一个介于0到1之间的实数； P=0，表示事件A一定不会发生，而P=1，则表示事件A一定会发生。

以掷骰子为例，由于骰子为6面，任意一面上点数发生的概率都是相同。所以，事件A：掷出点数为1的概率为：

对比而言，Odds指的是事件发生的概率与事件不发生的概率 之比：

还拿掷骰子的例子说事，掷出点数为1的Odds为：

很明显，Odds和概率之间的关系为：

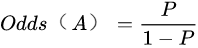
进一步简化可知，

换句话说，事件A的Odds 值，等于 事件A出现的次数 和 其它（非A）事件出现的次数 之比。

相比而言，事件A的概率值， 等于事件A出现的次数 与 所有事件的次数 之比。

很容易推导得知：

概率P（A）和Odds（A）的值域是不同的。前者被锁定在[0,1]之间，而后者则是  .

那这说了半天，这和Logit到底有什么关系呢？

请注意Logit一词的构词分解，它的含义是对它（it）取对数（Log），这里“it”就是指Odds。下面我们就可以给出Logit的定义了：

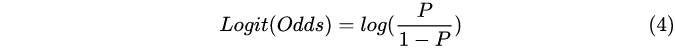
公式（4）实际上就是所谓Logit变换。

2.Logit变换的意义在哪里

与概率不同的地方在于，Logit的一个很重要的特性，就是它的值域没有上下限，如图1所示。

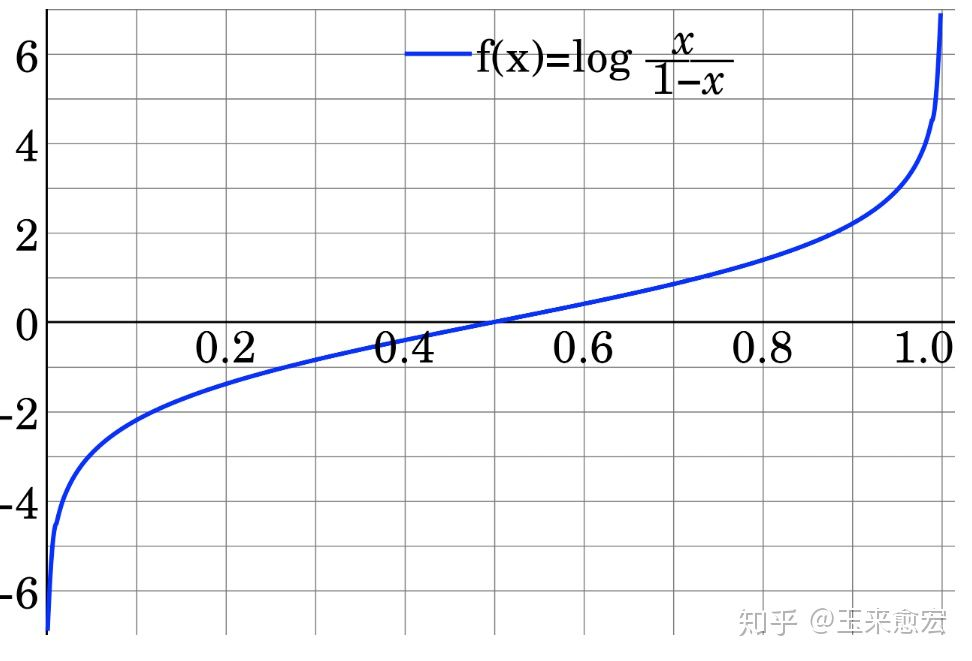
                                                    图1 Logit的示意图

从图1可以看出，通过变换，就给建模提供了方便。

想象这么一个场景，我们想研究某个事件A发生的概率P，P值的大小和某些因素相关，例如研究有毒药物的使用剂量大小（x）和被测小白鼠的死亡率（P）之间的关系。

很显然，死亡率P和x是正相关的，但由于P的值域只能在[0,1]之间，而x的取值范围要宽广得多。因此，P不太可能是x的线性关系或二次函数，一般的多项式函数也不太适合，这就给此类函数的拟合（回归分析）带来麻烦。

此外，当P接近于0或1的时候，即使一些因素变化很大，P的值也不会有显著变化。

例如，对于高可靠系统，其可靠度P已经是0.997了，倘若再改善条件、提高工艺和改进体系结构，可靠度的提升只能是小数点后三位甚至后四位，单纯靠P来度量，已经让我们无所适从，不知道改善条件、提高工艺和改进体系结构到底有多大作用。

再比如，宏观来看，灾难性天气发生的概率P非常低（接近于0），但这类事件类似于黑天鹅事件（特征为：影响重大、难以预测及事后可解释），由于概率P值对接近于0的事件不敏感，通过P来度量，很难找到刻画发生这类事件的前兆信息。

这时，Logit函数的优势就体现出来了。从图1可以看出，在P=0或P=1附近，Logit非常敏感（值域变化非常大）。通过Logit变换，P从0到1变化时，Logit的值域为正负无穷。正是由于Logit值域的不受限，让回归拟合变得容易了！

通常，Logit对数的底是自然对数e，这里我们把Odds用符号  表示，则有：

显然，从公式（5）我们也容易推导出概率P的值：

通常，我们先借助Logit变换，让我们方便拟合数据（即logistics回归），然后再变换回我们熟悉的概率。就是这么一个循环，为数据分析提供了便利。某种程度上，这类变换，非常类似于化学中的催化剂。

在化学反应里，催化剂能改变反应物化学反应速率而不改变化学平衡，且本身的质量和化学性质在化学反应前后都没有发生改变。

如果我们在把公式（6）做一下变形，如分子和分母同乘以  ，可得到公式（7）：

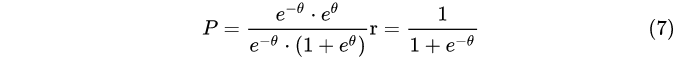
是的，聪慧如你，你一定看出来了，公式（7）就是在神经网络广泛使用的Sigmoid 函数，又称对数几率函数（ logistic function ）。

通常，我们把公式（5）表示的便于拟合的“概率替代物”称为logits。事实上，在多分类（如手写识别等）中，某种分类器的输出（即分类的打分），也称为logits，即使它和Odds的本意并没有多大联系，但它们通过某种变换，也能变成“概率模型”，比如下面我们即将讲到的Softmax变换。

3. TensorFlow中的Softmax函数

再回到softmax函数的讨论上。

tf.nn.softmax_cross_entropy_with_logits(
    _sentinel=None,
    labels=None,
    logits=None,
    dim=-1,
    name=None
)

这个函数的功能就是，计算labels（通常是one-hot编码表征的概率）和 logits 经过变换后对应概率之间的交叉熵（cross entropy）。

第一个参数基本不用。此处不说明。

第二个参数 label 的含义就是一个分类标签，所不同的是，这个label是分类的概率，比如说[0.2,0.3,0.5]，labels的每一行必须是一个概率分布。

现在来说明第三个参数logits，logit的值域范围 [-inf,+inf]（即正负无穷区间）。如前所述，我们可以把logist理解为原生态的、未经缩放的，可视为一种未归一化的“概率替代物”，如[4, 1, -2]。它可以是其他分类器（如逻辑回归等、SVM等）的输出。

比如说，上述向量中“4”的值最大，因此，属于第1类的概率最大，“1”的值次之，所以属于第2类的概率次之。

交叉熵（Cross Entropy）是Shannon信息论中一个重要概念，主要用于度量两个概率分布间的差异性信息。

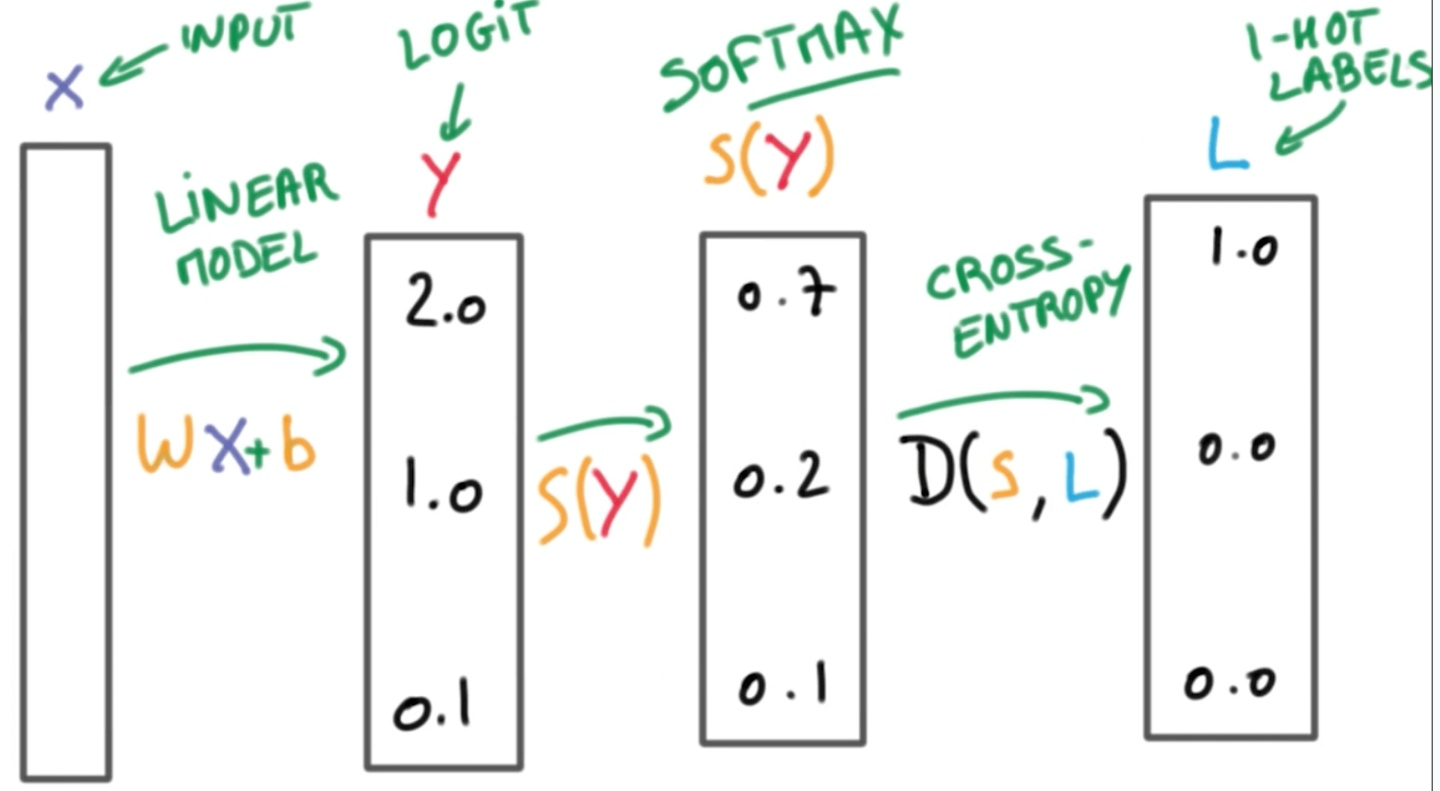
由于logits本身并不是一个概率，所以我们需要把logits的值变化成“概率模样”。这时Softmax函数该出场了。Softmax把一个系列的概率替代物（logits）从[-inf, +inf] 映射到[0,1]。除此之外，Softmax还保证把所有参与映射的值累计之和等于1，变成诸如[0.95, 0.05, 0]的概率向量。这样一来，经过Softmax加工的数据可以当做概率来用（如图2所示）。

                                                  图2 Softmax的工作原理

经过softmax的加工，就变成“归一化”的概率（设为p1），这个新生成的概率p1，和labels所代表的概率分布（设为p2）一起作为参数，用来计算交叉熵。

这个差异信息，作为我们网络调参的依据，理想情况下，这两个分布尽量趋近最好。如果有差异（也可以理解为误差信号），我们就调整参数，让其变得更小，这就是损失（误差）函数的作用。

最终通过不断地调参，logit被锁定在一个最佳值（所谓最佳，是指让交叉熵最小，此时的网络参数也是最优的）。softmax和交叉熵的工作流程如图3所示

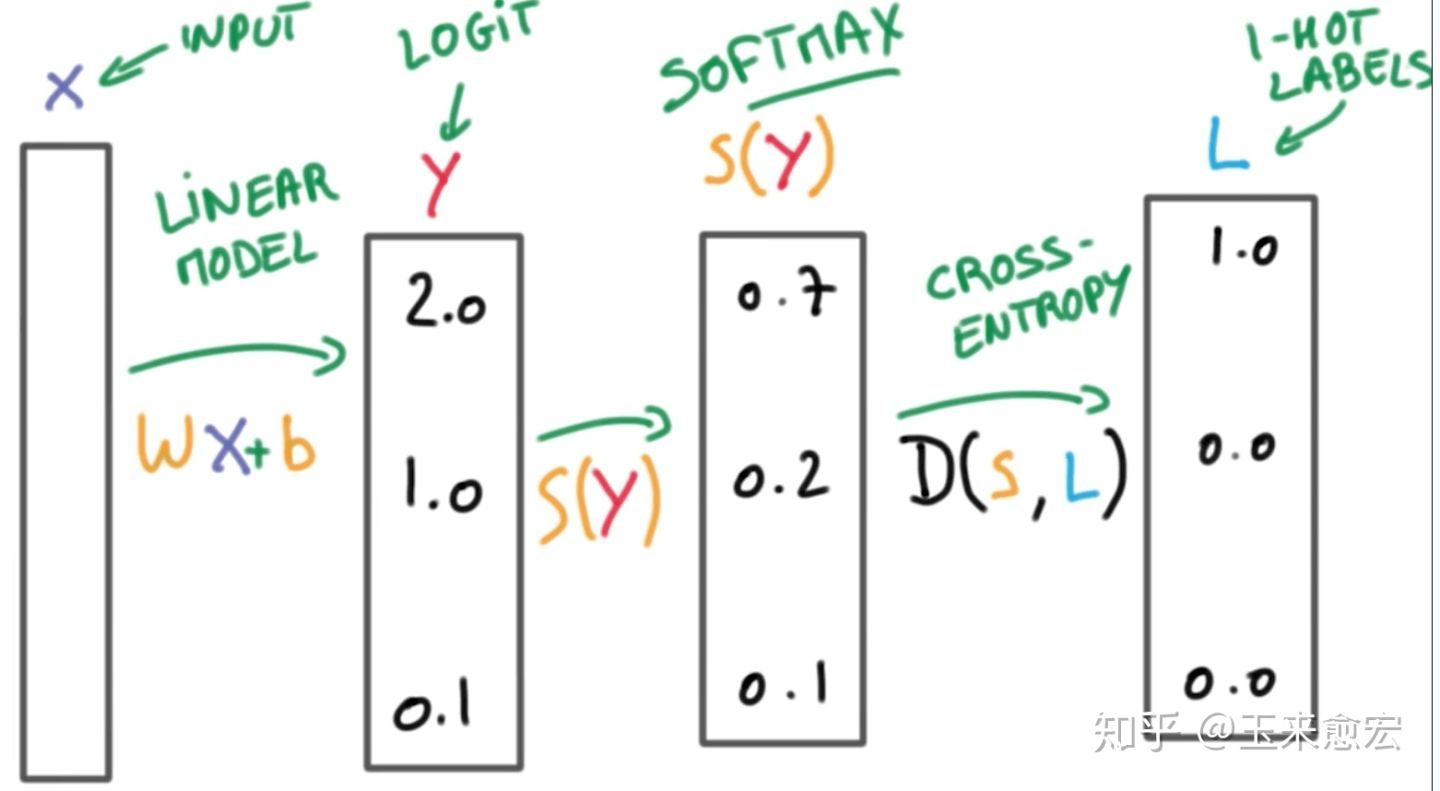
                                                图3  Logit、Softmax与交叉熵的工作流程（图片来源：互联网）

从图3可以看出，针对输入，分类器可以计算一个logit值，logit值通过Softmax处理变成概率，该概率再和One-Hot（独热编码）对应的概率一起计算交叉熵，这个交叉熵用来调节网络参数。

为什么One-Hot（独热编码）可以看做一种概率呢？下面我们也简单介绍一下。

One-Hot编码，又称为“一位有效编码”，它主要是采用位状态寄存器的思想，来对状态进行编码，在任意时候，只有一位有效，设值为1，其他位均为0。

在本例中，我们就用一个1×10的“One Hot”向量代表标签（label）信息，数字n就对应第n位为1。举例来说，数字0对应的向量就是[1,0,0,0,0,0,0,0,0,0]，数字1对应的矩阵就是[0,1,0,0,0,0,0,0,0,0]，..., 数字9对应的矩阵就是[0,0,0,0,0,0,0,0,0,9]，以此类推。

这里，我们把1理解为100%，0理解为0%，那么[0,0,0,0,0,0,0,0,0,1]就表示，在训练集中，属于数字9的概率为100%。

就这样，一个原本代表标签（label）的分类信息，被巧妙的当成了概率使用。

于是，它就可以和分类器经过Softmax加工给出的预测概率联合起来，计算交叉熵，从而再依据这个交叉熵进行反向调参。

很显然，如果One-Hot给出的预期概率，和logits经过softmax给出的预测概率，二者之间的差异越小，那么交叉熵就越小，调参就越趋近最佳。

下面我们列举一个案例说明：

#!/usr/bin/env python3
# -*- coding: utf-8 -*-
"""
Created on Thu May 10 08:32:59 2018
@author: yhilly
"""

import tensorflow as tf

labels = [[0.2,0.3,0.5],
          [0.1,0.6,0.3]]
logits = [[4,1,-2],
          [0.1,1,3]]

logits_scaled = tf.nn.softmax(logits)
result = tf.nn.softmax_cross_entropy_with_logits(labels=labels, logits=logits)

with tf.Session() as sess:
    print (sess.run(logits_scaled))
    print (sess.run(result))

运行结果：

[[0.95033026 0.04731416 0.00235563]
 [0.04622407 0.11369288 0.84008306]]

[3.9509459 1.6642545]

需要注意的是：

（1）如果labels的每一行是one-hot表示，也就是只有一个地方为1（或者说100%），其他地方为0（或者说0%），还可以使用tf.sparse_softmax_cross_entropy_with_logits()。之所以用100%和0%描述，就是让它看起来像一个概率分布。

（2）tf.nn.softmax_cross_entropy_with_logits（）函数已经过时 (deprecated)，它在TensorFlow未来的版本中将被去除。取而代之的是

tf.nn.softmax_cross_entropy_with_logits_v2（）

(3)参数labels,logits必须有相同的形状 [batch_size, num_classes] 和相同的类型(float16, float32, float64)中的一种，否则交叉熵无法计算。

（4）tf.nn.softmax_cross_entropy_with_logits 函数内部的 logits 不能进行缩放，因为在这个工作会在该函数内部进行（注意函数名称中的 softmax ，它负责完成原始数据的归一化），如果 logits 提前进行了缩放（归一化），那么反而会影响计算正确性。

-------------------------------------------

本文部分节选自《深度学习之美：AI时代的数据处理与最佳实践》（张玉宏著，电子工业出版社，2018年7月出版）。更多理论推导及实战环节，请参阅该书。

---------------