代码随想录Day22

77. 组合

给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。

你可以按 任何顺序 返回答案。

示例 1：

输入：n = 4, k = 2
输出：
[
  [2,4],
  [3,4],
  [2,3],
  [1,2],
  [1,3],
  [1,4],
]

示例 2：

输入：n = 1, k = 1
输出：[[1]]

提示：

1 <= n <= 20

1 <= k <= n

---

正解(回溯)

直接的解法当然是使用for循环，例如示例中k为2，很容易想到 用两个for循环，这样就可以输出 和示例中一样的结果。

输入：n = 100, k = 3 那么就三层for循环

如果n为100，k为50呢

此时就会发现虽然想暴力搜索，但是用for循环嵌套连暴力都写不出来

上面我们说了要解决 n为100，k为50的情况，暴力写法需要嵌套50层for循环，那么回溯法就用递归来解决嵌套层数的问题。

递归来做层叠嵌套（可以理解是开k层for循环），每一次的递归中嵌套一个for循环，那么递归就可以用于解决多层嵌套循环的问题了。

1. 递归函数的返回值以及参数
   
   在这里要定义两个全局变量，一个用来存放符合条件单一结果，一个用来存放符合条件结果的集合。
   
   函数里一定有两个参数，既然是集合n里面取k个数，那么n和k是两个int型的参数。
   
   然后还需要一个参数，为int型变量startIndex，这个参数用来记录本层递归的中，集合从哪里开始遍历（集合就是[1,...,n] ）。
2. 回溯函数终止条件
   
   什么时候到达所谓的叶子节点了呢？
   
   path这个数组的大小如果达到k，说明我们找到了一个子集大小为k的组合了，在图中path存的就是根节点到叶子节点的路径。
3. 单层搜索的过程
   
   回溯法的搜索过程就是一个树型结构的遍历过程，在如下图中，可以看出for循环用来横向遍历，递归的过程是纵向遍历。
   
   for循环每次从startIndex开始遍历，然后用path保存取到的节点i。

上代码(●'◡'●)

class Solution {
private:
    vector<vector<int>> result; // 存放符合条件结果的集合
    vector<int> path; // 用来存放符合条件结果
    void backtracking(int n, int k, int startIndex) {
        if (path.size() == k) {
            result.push_back(path);
            return;
        }
        for (int i = startIndex; i <= n; i++) {
            path.push_back(i); // 处理节点
            backtracking(n, k, i + 1); // 递归
            path.pop_back(); // 回溯，撤销处理的节点
        }
    }
public:
    vector<vector<int>> combine(int n, int k) {
        result.clear(); // 可以不写
        path.clear();   // 可以不写
        backtracking(n, k, 1);
        return result;
    }
};

组合问题是回溯法解决的经典问题，我们开始的时候给大家列举一个很形象的例子，就是n为100，k为50的话，直接想法就需要50层for循环。

从而引出了回溯法就是解决这种k层for循环嵌套的问题。

然后进一步把回溯法的搜索过程抽象为树形结构，可以直观的看出搜索的过程。

接着用回溯法三部曲，逐步分析了函数参数、终止条件和单层搜索的过程。

优化(剪枝)

来举一个例子，n = 4，k = 4的话，那么第一层for循环的时候，从元素2开始的遍历都没有意义了。 在第二层for循环，从元素3开始的遍历都没有意义了。



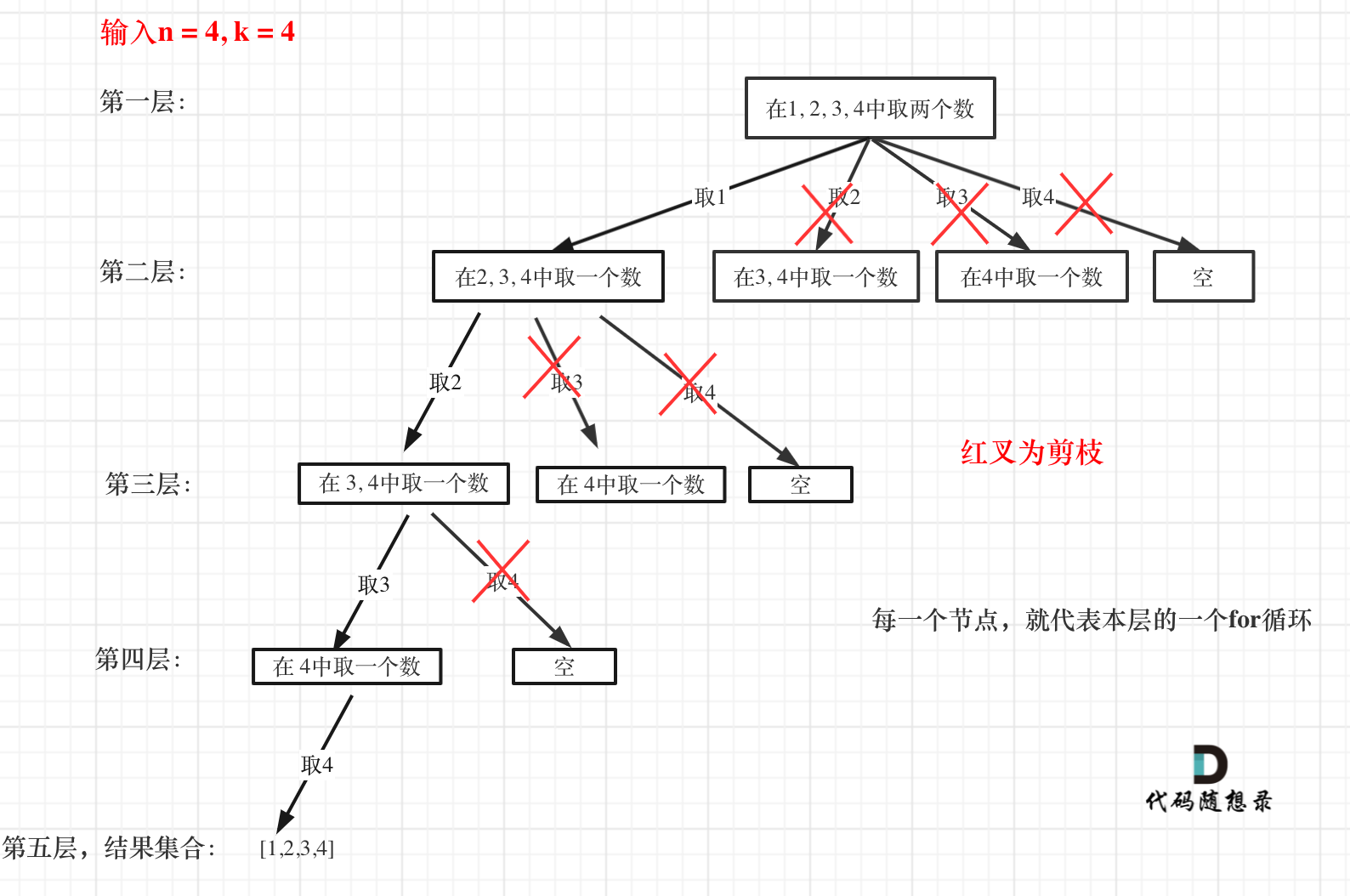
正如图所示，这种优化就像是把递归树上多余的枝杈剪掉了

图中每一个节点（图中为矩形），就代表本层的一个for循环，那么每一层的for循环从第二个数开始遍历的话，都没有意义，都是无效遍历。

所以，可以剪枝的地方就在递归中每一层的for循环所选择的起始位置。

如果for循环选择的起始位置之后的元素个数 已经不足 我们需要的元素个数了，那么就没有必要搜索了。

接下来看一下优化过程如下：

1. 已经选择的元素个数：path.size();
2. 还需要的元素个数为: k - path.size();
3. 在集合n中至多要从该起始位置 : n - (k - path.size()) + 1，开始遍历

优化代码(●ˇ∀ˇ●)

class Solution {
private:
    vector<vector<int>> result;
    vector<int> path;
    void backtracking(int n, int k, int startIndex) {
        if (path.size() == k) {
            result.push_back(path);
            return;
        }
        for (int i = startIndex; i <= n - (k - path.size()) + 1; i++) { // 优化的地方
            path.push_back(i); // 处理节点
            backtracking(n, k, i + 1);
            path.pop_back(); // 回溯，撤销处理的节点
        }
    }
public:

    vector<vector<int>> combine(int n, int k) {
        backtracking(n, k, 1);
        return result;
    }
};

写博不易，请大佬点赞支持一下8~