网络流与各种建模（I）

网络流基础

这里默认读者学习过网络流和MCMF，这里仅作复习

网络流解决的问题是给一个源点和汇点，每个边有最大流量，最大化从源点放水到汇点的速率。
网络流的时间复杂度是 $O(nm)$。对于一些建模可能跑得快一点，也就是跑不满。
Dinic 的做法是每次先给图 BFS 分层然后跑增广路，每次仅向层数比自身大的点流出。

时间复杂度的证明：不难发现每次 BFS 后的 $lv[t]$ 必然减少，否则仍然存在一条路径未流完，矛盾。每次增广路是 $O(m)$ 的，$lv[t]\leq n$ 所以时间上限是 $O(nm)$ 的。

Dinic 跑二分图最大匹配是 $O(m\sqrt n)$ 的，快于匈牙利的 $O(n^3)$。
我们可以通过跑完 dinic 后的流量变化判断每条边的流量从而构造方案。
使用的 dinic 封装模板（后面的参考代码默认加上该模板）

namespace graph{

const int MAXN=1e5+5;

const int MR=1e6+5;

int las[MAXN],cur[MAXN];

int lv[MAXN],N,s,t;

queue<int> q;

struct edge{

	int u,v,w,ne;

}e[MR];int tot=1;

void init(){

	tot=1;

	for(int i=1;i<=N;i++)

		las[i]=0;

}

void add(int u,int v,int w){

	++tot;

	e[tot].u=u,e[tot].v=v,e[tot].w=w;

	e[tot].ne=las[u],las[u]=tot;

	return;

}

void Add(int u,int v,int w){

	add(u,v,w);

	add(v,u,0);

}

bool BFS(){

	for(int i=1;i<=N;i++) lv[i]=-1;

	lv[s]=0;q.push(s);

	while(!q.empty()){

		int u=q.front();q.pop();

		for(int i=las[u];i;i=e[i].ne){

			int to=e[i].v,val=e[i].w;

			if(val&&lv[to]==-1){

				lv[to]=lv[u]+1;

				q.push(to);

			}

		}

	}

	return lv[t]!=-1;

}

ll dinic(int u,ll flow){

	if(u==t) return flow;

	ll rmn=flow;

	for(int i=cur[u];i&&rmn;i=e[i].ne){

		cur[u]=i;

		ll to=e[i].v,val=e[i].w;

		if(val>0&&lv[to]==lv[u]+1){

			ll c=dinic(to,min(rmn,val));

			rmn-=c;

			e[i].w-=c;

			e[i^1].w+=c;

		}

	}

	return flow-rmn;

}

ll max_flow(){

	ll ans=0;

	while(BFS()){

		for(int i=1;i<=N;i++)

			cur[i]=las[i];

		ans+=dinic(s,1e18);

	}

	return ans;

}

}

MCMF（费用流）解决的问题是在网络流问题的基础上每个边加上费用，最大化速率的同时要最小费用。
解决方法是把 BFS 分层换成 SPFA 费用分层。
时间复杂度是 $O(nV)$ 的，$V$ 是费用的和，证明同上。但是远远跑不满。
本篇文章使用的封装费用流模板如下：

namespace graph{

const int MAXN=1e5+5;

const int MR=1e6+5;

struct edge{

	int v,w,c,ne;

}e[MR];int cnt=1;

int las[MAXN],cur[MAXN];

int dis[MAXN];bool inq[MAXN],vis[MAXN];

int N,m,s,t;

queue<int> q;

void add(int u,int v,int w,int c){

	++cnt;

	e[cnt].v=v,e[cnt].w=w,e[cnt].c=c;

	e[cnt].ne=las[u],las[u]=cnt;

	return;

}

void Add(int u,int v,int w,int c){

	add(u,v,w,c);

	add(v,u,0,-c);

}

bool SPFA(){

	for(int i=1;i<=n;i++)

		dis[i]=1e9,inq[i]=0;

	dis[s]=0;q.push(s);

	while(!q.empty()){

		int u=q.front();q.pop();inq[u]=0;

		for(int i=las[u];i;i=e[i].ne){

			int v=e[i].v,val=e[i].w,cost=e[i].c;

			if(val&&dis[v]>dis[u]+cost){

				dis[v]=dis[u]+cost;

				if(!inq[v]){

					inq[v]=true;

					q.push(v);

				}

			}

		}

	}

	return dis[t]!=1e9;

}

int dfs(int u,int flow){

	vis[u]=true;

	if(u==t) return flow;

	int rmn=flow;

	for(int i=cur[u];rmn&&i;i=e[i].ne){

		cur[u]=i;

		int v=e[i].v,val=e[i].w,cost=e[i].c;

		if(val&&dis[v]==dis[u]+cost&&!vis[v]){

			int fl=dfs(v,min(val,rmn));

			rmn-=fl;

			e[i].w-=fl;

			e[i^1].w+=fl;

		}

	}

	vis[u]=false;

	return flow-rmn;

}

ll MCMF(){

	ll ans=0,res=0;

	while(SPFA()){

		for(int i=1;i<=n;i++)

			cur[i]=las[i],vis[i]=0;

		ll flow=dfs(s,1e9);

		ans+=flow,res+=flow*dis[t];

	}

	return res;

}

}

网络流最困难的地方是建模，也就是我们要把一个问题换成网络流问题。
对于一些没有思路的题，不妨想想网络流。

一些写容易忘记的点

在写 MCMF 时需要给 dinic 函数设立一个 vis 数组，表示当前点是否在 dinic 搜索中，以防有重复环。

网络流建模

二分图问题

二分图最大匹配问题

求二分图最大匹配。

要求 $O(\sqrt ne)$。

网络流的常见建模方式是建立超级源点和超级汇点。

在本题中我们建立超级源点 $s$ 和超级汇点 $t$。在原图基础上，$s$ 连所有左部点，所有右部点连 $t$。所有边流量为 $1$（这里保证了每个点、边都只会被使用一次）。

二分图最大权完美匹配问题

求二分图最大权完美匹配。没有输 -1。

$n\leq 300$。

在上题的基础上增加费用限制。源点汇点的边费用均为 $0$，中间边费用给定。跑一遍最大费用。

【例题】路径覆盖问题

给 DAG，求最少的路径覆盖所有点。路径不可重点。

$n\leq10^3$。

DAG 所提供的条件在于我们可以随便连一个没有入边的节点。

我们把问题转换成二分图最大匹配问题。一个节点拆成两个，一个匹配出边，一个匹配入边。这样答案就是点数减去匹配数。

【习题】P2763 试题库问题

$n$ 个物品，物品有多个标签。

构造，把一些物品分到标签类里面，给定每个标签类 $i$ 的大小 $r_i$。

$n\leq 10^3$，不同标签数 $\leq 20$。

【习题】P3254 圆桌问题

【习题】P2765 魔术球问题

有 $n$ 根柱子，依次进入 $1,2,\dots m$。

每个数放的柱子要和当前柱子顶部的数的和是完全平方数。

最大化 $m$，给构造。

$n\leq 55$。

【例题】最小链覆盖

给 DAG，求最少的路径覆盖所有点。路径可重点。

$n\leq10^3$。

传递闭包后跑路径覆盖即可。传递闭包使用 $\text{bitset}$ 优化做到 $O(\dfrac{n^3}{\omega})$。

这道例题可以看做一种偏序关系，定理 $\text{Dilworth}$ 告诉我们最小链覆盖等于最长反链。举个通俗的例子，最小严格上升子序列覆盖等于最长非严格下降子序列长度。

一些解释：一个 DAG（或偏序集）的反链指最大的点集，点集内两点都不可达。

我们使用 $\text{Dilworth}$ 定理练习练习。

【例题】P4298 [CTSC2008]祭祀

给 DAG，求反链长度，构造最长反链，问每个点是否可以作为最长反链一点。

$n\leq 100$。

第一问按照上面来，我们先讲第三问。

对于枚举点 $i$，我们删掉点 $i$ 和所有与 $i$ 有偏序关系的点，如果得到新图的答案恰比原图答案少 $1$，那么这个点可作为最长反链上一点，否则不行。

第二问我们贪心枚举每一个可以作为最长反链的点，每次选中一个 $i$ 就把 $i$ 和和 $i$ 有偏序关系的点全部删掉就可以了。

给一份参考代码：

#include<iostream>

#include<queue>

using namespace std;

#define ll long long

const int inf=1e9;

namespace graph{/*do sth.*/}

const int MAXN=105;

bool flag[MAXN][MAXN];

int n,m,s,t;

int ls[MAXN],rs[MAXN],tot=0;

bool p1[MAXN],p2[MAXN],chc[MAXN],used[MAXN];

int main(){

	s=graph::s=++tot;

	t=graph::t=++tot;

	cin>>n>>m;

	for(int i=1;i<=n;i++)

		ls[i]=++tot,rs[i]=++tot;

	for(int i=1;i<=m;i++){

		int u,v;cin>>u>>v;

		flag[u][v]=1;

	}

	for(int k=1;k<=n;k++)

		for(int i=1;i<=n;i++)

			for(int j=1;j<=n;j++)

				if(flag[i][k]&&flag[k][j])

					flag[i][j]=1;//传递闭包

	graph::N=tot;

	for(int i=1;i<=n;i++)

		graph::Add(s,ls[i],1),

		graph::Add(rs[i],t,1);

	for(int i=1;i<=n;i++)

		for(int j=1;j<=n;j++)

			if(flag[i][j])

				graph::Add(ls[i],rs[j],1);

	int ans=n-graph::max_flow();

	cout<<ans<<endl;

	for(int k=1;k<=n;k++){

		int cnt=0;

		graph::init();

		for(int i=1;i<=n;i++)

			if(flag[k][i]||flag[i][k]||k==i)

				p1[i]=1;

			else p1[i]=0;

		for(int i=1;i<=n;i++)

			if(!p1[i])

			cnt++,

			graph::Add(s,ls[i],1),

			graph::Add(rs[i],t,1);

		for(int i=1;i<=n;i++)

			for(int j=1;j<=n;j++)

				if(!p1[i]&&!p1[j]&&flag[i][j])

					graph::Add(ls[i],rs[j],1);

		if(cnt-graph::max_flow()==ans-1)

			chc[k]=1;

	}

	for(int i=1;i<=n;i++)

		if(chc[i]&&!used[i]){

			cout<<"1";

			for(int j=1;j<=n;j++)

				if(flag[i][j]||flag[j][i]||i==j)

					used[j]=1;

		}else cout<<"0";

	cout<<endl;

	for(int i=1;i<=n;i++) cout<<chc[i];

	return 0;

}

【例题】[SCOI2007] 修车

$m$ 个师傅修 $n$ 个车，每个师傅修每个车有不同的时间 $T_{i,j}$。

求所有顾客的最小平均等待时间。

$m\leq 9,n\leq 60$。

不难发现如果一个车 $c$ 是当前师傅 $i$ 倒数第 $k$ 个维修的，那么它对等待时间的贡献就是 $T_{i,j}\times k$。

我们考虑转成二分图，左边代表每一个车，右边代表每个师傅的状态（即师傅 $i$，倒数第 $j$ 个维修），中间连带权边表示左边的车给右边状态的师傅修的贡献。那么问题就变成了二分图最大匹配最小权。

跑费用流。

【引理】$\textbf{Konig}$ 定理

二分图最小点集覆盖等于最大匹配。

解释：二分图最小点集覆盖指选一些点使得每条边都有端点是标记点。

证明是显然的，留给读者。（提示，证明两个不等式，即左小等右，右小等左）。

【例题】UVA11419 SAM I AM

给 $n\times m$ 的方格，有一些标记点。

选择一些行、列使得每个标记点都在标记行或列上。

$n,m\leq10^3$。

利用 $\text{Konig}$ 定理转化成二分图最大匹配。

【引理】最大独立集

二分图最大独立集等于总点数减去最小点覆盖

证明：考虑最大独立集为 $S$。考虑每一条边，必然不能都是 $S$ 点，所以 $V-S$ 是最小点覆盖。

这些结论在二分图当中有一定作用。

【题型】选择限制问题

给一些元素，每个元素选或不选，选有奖励 $v_i$。

给一些限制 $u,v$ 表示 $u,v$ 不能都选。

* 特殊限制（一般是隐藏条件）限制构成二分图。

一般特殊条件难以注意（可能需要染色），如果注意到了就变成了最大独立集问题。

现在点有了权值，我们可以源点向左部点连边的容量是 $v_i$，右部点向汇点连边的容量为 $v_i$，原图边容量为 $\infty$。

【习题】P3355 骑士共存问题 黑白染色。

【习题】P5030 长脖子鹿放置 行染色。

利用最小割

【引理】最小割

最小割等于最大流

这里最小割的意思是割去最小边权和的边集使得图不连通。

利用最小割原理，我们可以搞些有趣的建模。

【题型】二者取一问题

给 $n$ 个选择，答案只有 $0/1$。两种选择都有不同的奖励权值。

给 $m$ 个奖励条件，第 $i$ 条形如如果一个集合的题全部选择 $0$（或者 $1$）。那么额外获得一定的奖励权值。

最大化奖励权值。

先考虑简单情况，也就是没有奖励的时候，可以建出下面这样的图：

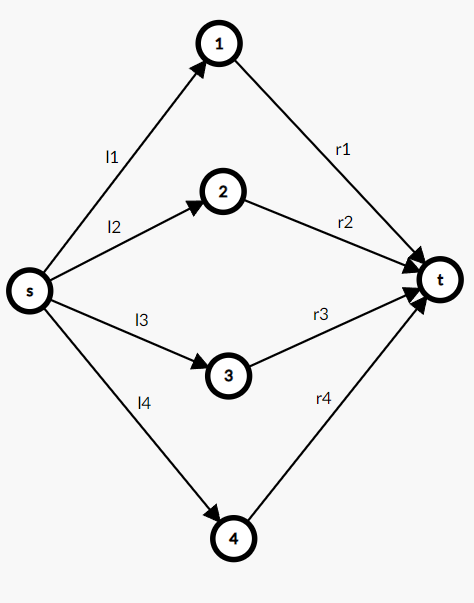
我们应该是想要所有边权减去最大流。

所为奖励本质上就是限制。也就是说如果你一个点集没有割完同一方向的边，那么你就要把奖励也给割掉。

也就是说当且仅当你把一边的边全部保留你才能不割奖励，不妨设是限制是全部选 $0$。那么可以建图如下：

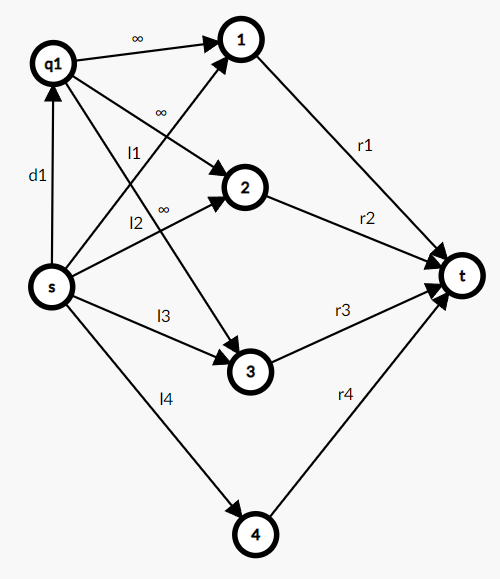
这里我们可以发现无穷边是不能割的，如果你选择保留了 $1,2,3$ 之一的 $1$ 选项，那么就会存在 $s\to q1\to u\to t$ 的路径，此时必须割掉奖励。

全部选 $0$ 同理。

【习题】P4313 文理分科 二者取一式问题的简单形式。

【习题】P1361 小M的作物 板子。

【题型】最大权闭合子图

定义有向图 $G$ 的闭合子图 $G'$ 为 $G'$ 中的点在 $G$ 中的出边终点都在 $G'$ 当中。

每个点有点权（可能为负）求最大权闭合子图。

建模方式是给源点连向所有正权点，所有负权点连向汇点，流量是点权绝对值。原图正常连边，流量为 $\infty$。

考虑最小割，割掉正权点表示不选择该点，割掉负权点表示选择该点，最终的答案为所有正权和减去最小割。

下面证明这一建模：考虑每一条路径 $s\xrightarrow{a} u\xrightarrow{\infty} v\xrightarrow{b} t $。有两种割的方式：

割 $a$ 留 $b$：表示不选择 $u$ 也不选择 $v$。
留 $a$ 割 $b$：表示选择 $u$ 也选择 $v$。

刚好是闭合子图的形式，剩下还有一种形式：

不选 $u$ 但选 $v$

的形式必然不优，证明完毕。

【习题】P3872 [TJOI2010]电影迷

给有向图，点有点权，边有边权。

求极多边子图，最大化点权减边权。

$n\leq 100$，保证边权为正。

提示：如果边权是 $\infty$ 就可以转化成最大权闭合子图，可以考虑在最大权闭合子图的建模上改造。

【习题】P2762 太空飞行计划问题 二分图上跑最大权闭合子图。

【习题】 UVA1389 Hard Life 最大密度闭合子图。

提示：二分密度 $\rho$，所有点权减去 $\rho$ 跑最大权闭合子图，看权是否 $>0$ 即可。

拆点法

【例题】P1402 酒店之王

$n$ 个人，每个人有自己喜欢的一些饮料和食物。每种饮料和食物只有一份。

合理安排，最大化饮料食物都喜欢的人数。

$n,p,q\leq100$。

同上面的建模思路，我们分成三部点，左边时饮料，中间是人，右边是食物。超级源点向饮料连，饮料向喜欢的人连，人向食物连，食物向超级汇点连，所有边流量为 $1$。

跑网络流发现一个问题，一个人可能同时被多个食物或饮料匹配上，这是因为每个人也是有限制的。

一般来说我们解决点的限制可以拆点转为边的限制。

本题中我们每个人开一个副本，饮料连本体，本体连副本，副本连食物即可。大概可以建出来这样的图

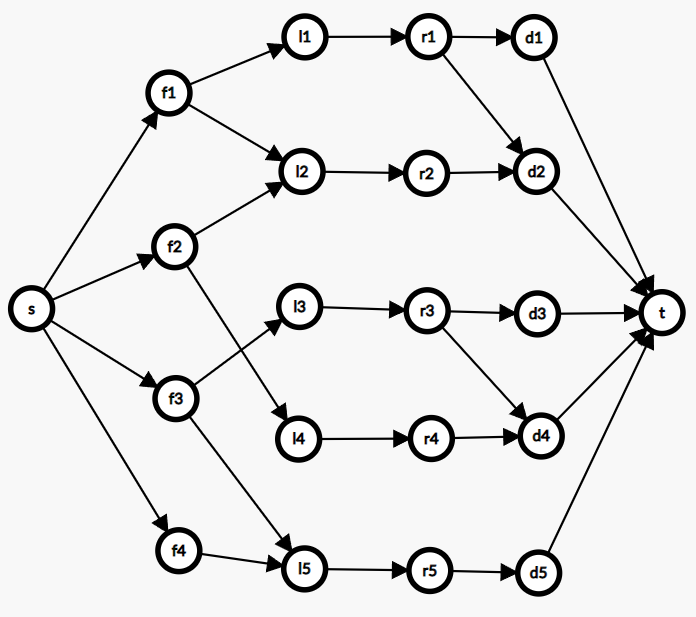
跑网络流。

【例题】P1345 [USACO5.4]奶牛的电信

给定无向图，问最少删多少点才能使 $c_1,c_2$ 不连通（不能删 $c_1,c_2$）。

$n\leq 100,m\leq600$。

我们在利用最小割的时候要清楚哪些边可以割，哪些边不能割。

本题我们主要是研究点，我们先把点拆称 $l_u,r_u$，超级源点连向 $l_u$，$r_u$ 连向超级汇点。由于需要割点，所以 $l_u\to r_u$ 连容量为 $1$ 的边，特别的，若 $u\in\{c_1,c_2\}$ 那么容量也要设为 $\infty$。

对于边 $(u,v)$ 来说他是不能割的，所以对 $r_u\to l_v,r_v\to l_u$ 都设 $\infty$ 的容量。

跑网络流。

【习题】P3171 [CQOI2015]网络吞吐量

【习题】P3866 [TJOI2009] 战争游戏

平面图最大流问题

【引入】平面图与对偶图

平面图：存在以同构图 $G$ 使得任意两边仅在节点处相交。

对偶图：把平面图的面试做点，分割两个面的边试做边的图。

举个栗子，下图中原图 $G$ 和对偶图 $G'$ 都是平面图，$G'$ 是 $G$ 的对偶图。

平面图有个很好的性质，就是平面图的最小割等于对偶图的最短路。

拿上面的图来说，我们要求 $2,5$ 的最小割，可以建下面这样的对偶图：

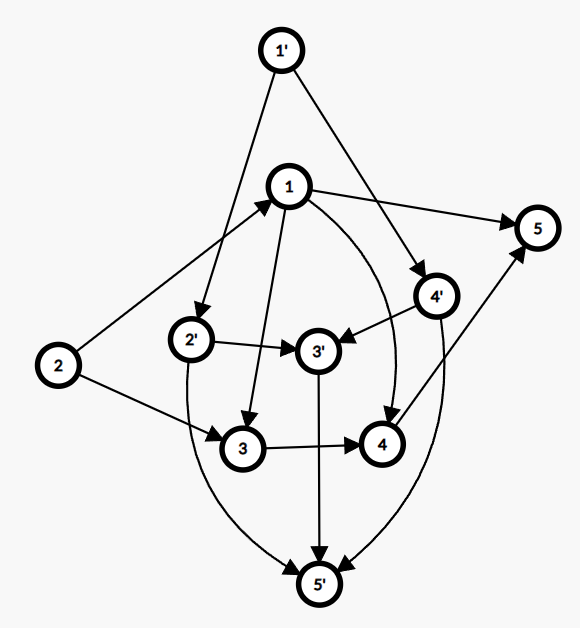
对偶图有两个外部点，作为起点和终点，是把直线 $2,5$ 连出来把平面分成两部分而成的。最短路最小性显然。

【例题】P2046 [NOI2010] 海拔

给一个 $n\times n$ 的网格图，每条边沿南北或东西。你知道每条边两个方向的客流量。

把 $n\times n$ 个节点黑白染色，要求 $(1,1)$ 染黑，$(n,n)$ 染白。

最小化从黑节点进入白节点的客流量。

$n\leq 500$。

标准的平面图，显然的是黑白两个色块必然连续，也就是我们必然可以在对偶图上找到一条路径分开 $(1,1),(n,n)$ 且路径上所有边在平面图中所对应的都是黑白边。

下图是一个参考的例子。

【习题】P4001 [ICPC-Beijing 2006] 狼抓兔子

给流赋予意义

在上面的例子中，网络流当中的“流”似乎只是一种工具，下面介绍几道把“流”视作为选择等有意义的事物的题目。

【例题】P3980 [NOI2008] 志愿者招募

给你 $m$ 种段，每种段形如 $[l_i,r_i]$，代价是 $w_i$。每种段都有无限个。

选代价最小的段使得每个位置 $i$ 的段数都不小于 $a_i$。

保证有解。

$n\leq10^3,m\leq10^4$。

我们把“流”看做每个人的选取情况

当你想不到什么好的做法时不如想想万能做法网络流。

本题当中每一个段他都对应一个区间，而且取了一个段就要区间加，这不符合二分图的建图。

我们考虑这事一个 DAG，我们把位置 $i$ 变成边 $i\to i+1$，费用应该为 $0$。但是这里流量比较奇怪，要的是不小于，我们先放一边，我们应该需要的是费用。

每个端 $[l_i,r_i]$ 的建模方式应该是 $l_i\to r_i+1$，表示跳过一个 $[l_i,r_i]$，流量是 $\infty$，费用是 $w_i$。猜测最终的流量应当是定值 $c=\infty$。

我们考虑每个位 $i$ 来说它必须有 $a_i$ 个位不经过它，转化一下就变成了最多只能容纳 $c-a_i$ 个流，这个作为上面的流量即可。

注意，我们这样子建模可能让答案不为 $c$，需要加上一个超级源点 $s\to 1$，汇点 $n+1\to t$。边权为 $c$。

妙妙妙。

【例题】P3358 最长 $\textbf{k}$ 可重区间集问题

若干开区间，最大化选取的开区间长度之和使得每个位置覆盖区间不超过 $k$。

$k\leq n\leq 500$。

我们把“流”试做为每个线段的选取情况。

先显然的离散化，长度变成权值，假设值域为 $w$。

按照上面的套路，我们尝试先建一个长度为 $w$ 的链表示 $[1,w]$ 每个长度为 $1$ 的开区间，流量是 $k$，费用是 $0$。

每个给定开区间 $[l,r]$ 给节点 $l,r$ 连边，流量是 $1$ 费用是 $len$。这样一个流量经过代表选择了这条边，反之亦然。

跑最大费用即可。

【例题】P1251 餐巾计划问题

你要进行 $n$ 天的营业，第 $i$ 天会使用 $r_i$ 的餐巾。

每天结束，你会把用完的餐巾交给快洗店（等待天数 $d_1$，费用 $r_1$）或慢洗店（等待天数 $d_2$，费用 $r_2$）或留下来等明天。

每天开始你也可以选择以 $p$ 的价格购入新的餐巾。

最小化价格。

$n\leq 2000$。

把“流”视为每个餐巾。

每天早上我们要购入一些餐巾，每天早上要向晚上送 $r_i$ 的餐巾，每天晚上可以给后面 $d_1,d_2$ 天的早上提供若干餐巾，显然的把每天拆成早上和晚上。

有个小问题，就是发现源点给早上提供的餐巾是 $\infty$，到了晚上如果流回去某天的早上那么这个流就会经过早晚边两次，这个建图的早晚边是流量瓶颈，这样肯定够不成最大流，换句话说这个模型求出来的最大流是不会换洗的。

这个图的缺点在于流不能从晚上的点流回去早上的点，但是我们发现每个晚上的点需求是固定的 $r_i$。我们反过来把晚上的点设为左点，早上的点设为右点，这样每个右点需要给汇点提供 $r_i$ 流量，左点从源点获得 $r_i$ 流量，左点流量可以向下传递，右点也可以直接从源点获得 $\infty$ 流量、费用 $p$（购入餐巾），左点 $i$ 也可以向 $i+d_j$ 的早晨提供若干费用为 $v_i$ 的流量（换洗）。建模完成。

int main(){

	int ls[MAXN],rs[MAXN],s,t,val[MAXN],tot=0;

	int n,p,d1,v1,d2,v2;

	cin>>n;

	for(int i=1;i<=n;i++) cin>>val[i];

	cin>>p>>d1>>v1>>d2>>v2;

	s=graph::s=++tot;

	t=graph::t=++tot;

	for(int i=1;i<=n;i++)

		ls[i]=++tot,rs[i]=++tot;

	for(int i=1;i<=n;i++){

		graph::Add(s,ls[i],val[i],0);

		graph::Add(s,rs[i],inf,p);

		graph::Add(rs[i],t,val[i],0);

		if(i+d1<=n) graph::Add(ls[i],rs[i+d1],inf,v1);

		if(i+d2<=n) graph::Add(ls[i],rs[i+d2],inf,v2);

		if(i<n) graph::Add(ls[i],ls[i+1],inf,0);

	}

	graph::N=tot;

	cout<<graph::MCMF();

	return 0;

}

其他的建模方法

【例题】P2754 [CTSC1999]家园 / 星际转移问题

有 $m$ 个交通工具每一时刻循环经过若干指定站。（不同的站不超过 $n+2$ 个）

把 $k$ 个人从站 $0$ 运送到站 $-1$ 的最小需要时间。

$n\leq 13,m\leq 20,k\leq 50$。

对时间分层建模，我们对于每个站的每个时刻状态建模。

枚举需要达成的时刻 $T$（这里可以二分，但是没必要），对于一开始站 $0$ 在 $0$ 时刻有 $k$ 点流量，建模不断让他往时刻大的它本身流动，跑最大流即可。

时间不会超过 $nk$，时间复杂度是 $O(n^4k^4)$ 远远跑不满。

【习题】P6054 [RC-02] 开门大吉

$n$ 个题，每题 $m$ 个选项，每个选项有对应奖励值 $p_{i,j}$。

若干限制，要求第 $u_i$ 题比 $v_i$ 题选择的编号至少多 $k_i$。

$n,m,p\leq 80$。

提示：这里 $n,m$ 小得可怜，时间、空间却大的离谱。能不能对每一个题目对应选择的状态看做一个点？

【例题】P2045 方格取数加强版

搞 $k$ 条从 $(1,1)$ 到 $(n,n)$ 的每次只能向右、下的路径。

求经过点权之和最大（经过多次只算一次）。

$n\leq 50$。

有个难搞的地方叫做经过多次只算一次。我们介绍一个模型我们叫做流量限制模型，如下：

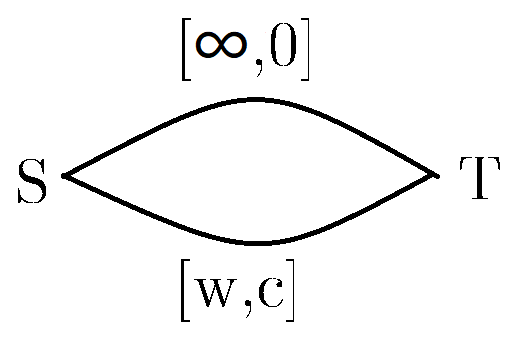
这种建模跑最大费用的时候，前 $w$ 的流量肯定会经过费用为 $c$ 的边，后面的只能进入费用为 $0$ 的边，目的达成。

本题中对方格分点即可。

【例题】P3163 [CQOI2014]危桥

给一个双向图，一些边是好边，可以经过无穷次，一些是坏边，只能经过 $2$ 次。

问：小 A、小 B 分别从 $s_1,s_2$ 出发，终点在 $t_1,t_2$ 要分别走 $k_1,k_2$ 个来回，是否可行。

$n\leq 50$，多测。

建图是显然的，如果是好边则连 $\infty$ 流量，否则连 $2$ 流量。本题显然是一个多原、汇网络流。

我们先说结论：

对 $s_1,s_2$ 作为源点，$t_1,t_2$ 作为汇点，分别拥有 $2k_1,2k_2$ 的流量；
对 $s_1,t_1$ 作为源点，$s_2,t_2$ 作为汇点，分别拥有 $2k_1,2k_2$ 的流量。

若以上两图都有 $2(k_1+k_2)$ 的最大流，那么可行；否则不可行。下面给出证明：

若答案有解，那么程序必然判断有解：这是显然的。

若程序判断有解，那么答案有解：考虑两个跑完的图的使用网络图为 $W_1,W_2$，那么 $\dfrac{W_1+W_2}2$ 可以得到 $s_1\to t_1$ 的流量使用情况，$\dfrac{W_1-W_2}{2}$ 可以得到 $s_2\to t_2$ 的流量使用情况。如果情况不合法，也就是有一个边，两个网络的使用情况为 $d_1,d_2$ 则 $|d_1|+|d_2|\geq 2$。这种情况取 $d_2'$ 和 $d_1$ 同号，数值与 $d_2$ 相同，那么 $|d_1+d'_2|\geq 2$ 也就是上述两种情况中有一种不可取，矛盾。故成立。

总结

这个博客的题目量很大，有时间自己写写题。

弱鸡还不会上下界，等一段时间补上下界，这也是为什么这个博客的标题带 （I）。