平衡二叉树（AVL）插入结点后的再平衡思路

理解平衡二叉树

在解决平衡二叉树动平衡问题，我们先来明确什么是平衡二叉树：

平衡二叉树是二叉搜索树的一种特殊情况，所以在二叉搜索树的基础上加上了如下定义：

平衡因子：我们将二叉树中各个结点的左右子树的高度差称为该节点的平衡因子。

平衡二叉树：就是在二叉搜索树的基础上，所有结点的平衡因子都小于等于一。则称该树为一颗平衡二叉树。

当然平衡二叉树有很多实现方案，例如：AVL、红黑树等。这篇文章还是以最基础的AVL方式实现一个自平衡二叉树。

例如：

在上图中10节点左子树高度为2,10的右子树高度为1，同样的我们查看5号结点的平衡因子等于0,15号结点的平衡因子为0，4号结点.............所以这棵树为平衡二叉树。

规律：当我们插入节点时，我们可以发现这么一个规律，被破坏平衡的节点最近也是插入节点的爷爷结点。

例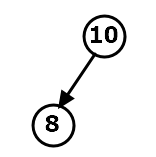：这棵树本来是一个平衡二叉树，如果我们插入一个值为6的结点，那么10号结点的平衡因子就会大于1，那么

这树就变得不平衡了。不平衡的节点为10，是6的爷爷结点。这是最极端的情况，不可能找到插入节点使得父结点不平衡的情况。（这句话自己好好体会）

插入节点的再平衡的解决思路

在AVL中采用节点的旋转使得树再平衡，二叉搜索树中节点的旋转不会破坏二叉搜索树的规则。

而平衡二叉树插入节点后导致平衡性被破坏，分为下面几种情况：（红色为不平衡节点，蓝色为刚刚插入的节点）

左左型：

右右型：

右左型：

左右型：

上面四种情况的再平衡需要做不同的讨论：

左左型的再平衡：

对于左左型，我们需要以被破坏平衡的节点为中心顺时针旋转，这样既没有破坏二叉搜索树的规则还，使得树再次平衡了。

这里我们举个栗子：

我们给定一个平衡二叉树：

现在我们插入一个值为1的结点：

此时导致节点为10的结点不平衡，而此时3、5、10节点正好形成左左型不平衡。按照上面的思路，我们需要以被破坏平衡的结点的位置为中心，旋转元素。

此时我们需要注意6号结点，该节点原先在5号结点的右孩子，但是由于旋转后原先的父节点肯定是5好节点的右孩子，占了5号结点的位置，但是又与10号结点被旋转后左孩子为空，我们刚好可以把它加入10结点的左孩子上（符合二叉搜索树的左小右大原则）。这样二叉树再次平衡了。

同样的右右型原理与左左型相同，此处不再赘述。

左右型的再平衡：

对于左右型，我们需要将破坏平衡结点的孩子节点和孙子节点进行逆时针旋转，这样就将问题又转换成了左左型。

此时我们只需要重复上面的左左型操作即可。

我们还是来举个栗子：

还是上面给出的那个平衡二叉树：

现在我们想要插入一个值为7的节点：

此时由于7号结点加入，10号几点变得不平衡了，而5、9、10节点也形成了“左右型”。此时我们只需要以10的孩子结点5的位置为中心，逆时针旋转。

此时问题转换成“左左型”的问题了（注意），那我们此时已10号结点为中心顺时针旋转即可解决这个问题

思路总结

在插入节点后我们需要以插入的节点为起点，向上寻找第一个不平衡节点，然后判断这个不平衡节点在不平衡路径上是哪种状态，然后根据不同的状态进行调整，如果是左左型或是右右型只需经过一次旋转即可，如果是左右型或者右左型需要先旋转一次将其转换成左左型或者右右型，然后再旋转一次即可使得二叉树平衡。

代码实现

二叉搜索树的实现：

public class MyBinarySearchTree {
    public static class Node {
        public int value;
        public Node lchild;
        public Node rchild;
        public Node parent;

        public Node(int value) {
            this.value = value;
        }
    }

    protected Node root;

    private int size = 0;

    public void insert(int value) {
        Node insertNode = new Node(value);
        if (root == null) {
            root = insertNode;
        } else {
            Node node = root;
            while (true) {
                if (value < node.value) {
                    if (node.lchild == null) {
                        node.lchild = insertNode;
                        insertNode.parent = node;
                        break;
                    }
                    node = node.lchild;
                } else {
                    if (node.rchild == null) {
                        node.rchild = insertNode;
                        insertNode.parent = node;
                        break;
                    }
                    node = node.rchild;
                }
            }
        }
        size++;
    }

    /**
     * 中序遍历
     */
    public List<Integer> inorderTree() {
        List<Integer> list = new LinkedList<>();
        inorderTree(list, root);
        return list;
    }

    private void inorderTree(List<Integer> list, Node node) {
        if (node != null) {
            inorderTree(list, node.lchild);
            list.add(node.value);
            inorderTree(list, node.rchild);
        }

    }

    public Node getNode(int value) {
        Node node = root;
        Node result = null;
        while (node != null) {
            if (node.value == value) {
                result = node;
                break;
            } else {
                if (value < node.value) {
                    node = node.lchild;
                } else {
                    node = node.rchild;
                }
            }
        }
        return result;
    }

    public Integer min() {
        return min(root).value;
    }

    public Node min(Node node) {
        if (node != null) {
            while (node.lchild != null) {
                node = node.lchild;
            }
            return node;
        }
        return null;
    }

    public Integer max() {
        Node node = root;
        if (node != null) {
            while (node.rchild != null) {
                node = node.rchild;
            }
            return node.value;
        }
        return null;
    }

    /**
     * 删除节点
     *
     * @param value
     */
    public void remove(int value) {
        /**
         * 解题思路：删除节点要分为三种情况
         *
         * 情况一：删除叶子节点  好解决
         * 情况二：删除单分支节点  由后面的元素顶替要删除的元素即可
         * 情况三：删除双分支节点，这种情况是最不好想的
         *       这种情况需要找到左子树最大的节点或右子树最小的节点顶上去。
         */
        Node node = this.getNode(value);
        if (node != null) {
            //当节点为叶子节点
            if (node.lchild == null && node.rchild == null) {
                //要删除的节点为根节点
                if (node.parent == null) {
                    root = null;
                }else{
                    //判断当前节点是父节点的左孩子还是右孩子
                    if (node.parent.rchild == node) {
                        node.parent.rchild = null;
                    } else {
                        node.parent.lchild = null;
                    }
                    node.parent = null;
                }
            } else if (node.lchild == null || node.rchild == null) {
                //当该节点为单分支节点

                //找到在单分支情况下,唯一的那个孩子节点
                Node childen = null;
                if (node.lchild != null) {
                    childen = node.lchild;
                    node.lchild = null;
                } else {
                    childen = node.rchild;
                    node.rchild = null;
                }

                //如果要删除的节点为根节点
                if (node.parent == null) {
                    root = childen;
                }else {
                    childen.parent = node.parent;
                    //同样的需要先判断当前节点是父节点的左孩子还是右孩子
                    if (node.parent.rchild == node) {
                        node.parent.rchild = childen;
                    } else {
                        node.parent.lchild = childen;
                    }
                }
            } else {
                //双分支情况
                //获取右分支最小的节点
                Node minNode = min(node.rchild);

                //采用递归法删除最小的那个节点，为什么可以使用递归删除呢，因为前面获得的右分支中的最小节点，
                //一定是叶子节点，或者向右倾斜的单分支节点，所以采用递归删除即可（前面的步骤不就用于删除这两种情况的吗）。
                this.remove(minNode.value);

                //将已经被删除的“右子树最小值”的结点的值附到需要删除的值的节点上，这样就从表象上完成了对指定节点的删除
                node.value = minNode.value;
            }
        }
    }

    /**
     * 获取当前Node的后继元素，即比当前Node的值大，但最接近当前Node值的结点（或者说是获得中序遍历的下一个元素）
     * @param node
     * @return
     */
    public Node nextValue(Node node){
        /**
         * 解题思路：在通常情况下后继结点就是右子树中最大的元素，但是如果没有右子树那就复杂了，
         * 那后继结点就是依次遍历父结点，将自己作为左子树的第一个父结点就是我们找的后继结点。
         */
        if (node != null) {
            if (node.rchild != null) {
                return min(node.rchild);
            }else{
                while (node !=null && node.parent.rchild == node){
                    node = node.parent;
                }
                return node.parent;
            }
        }
        return null;
    }

    public boolean isBalance() {
        return false;
    }

    public int size() {
        return size;
    }

    public int getHeight(Node node) {
        if(node != null){
            if(node.lchild == null && node.rchild == null){
                return 0;
            }else{
                return 1+Math.max(getHeight(node.lchild),getHeight(node.rchild));
            }
        }
        return -1;
    }

    public int getHeight() {
        return this.getHeight(root);
    }

    /**
     * 判断当前节点是否是父节点的右孩子，如果没有父节点则返回null
     * @param node
     * @return
     */
    public static Boolean isRchild(Node node){
        if(node != null && node.parent != null){
            if(node.parent.rchild == node){
                return true;
            }
            return false;
        }else{
            return null;
        }
    }

    /**
     * 判断当前节点是否是父节点的左孩子，如果没有父节点则返回null
     * @param node
     * @return
     */
    public static Boolean isLchild(Node node){
        if(node != null && node.parent != null){
            if(node.parent.lchild == node){
                return true;
            }
            return false;
        }else{
            return null;
        }
    }
}

平衡二叉树的实现：（继承于二叉搜索树）

public class MyBalanceTree extends MyBinarySearchTree {
    /**
     * 解题思路：平衡二叉树我们需要先插入节点，然后从插入节点往上找，找到第一个不平衡的节点，看这个不平衡的树是什么类型的
     * 左左型 右右型
     * 左右型 右左型
     * <p>
     * 我们将不平衡节点设为g 不平衡节点的孩子节点设置p p的孩子节点设为s
     *
     * @param value
     */
    @Override
    public void insert(int value) {
        //先插入节点，然后在调整树的平衡
        super.insert(value);
        //获得刚刚插入的节点
        Node node = this.getNode(value);
        Node[] unBalance = this.getFirstUnbalanceNode(node);
        if (unBalance != null) {
            this.reBalance(unBalance);
        }
    }

    /**
     * 根据插入节点向上找到第一个未平衡节点
     *
     * @param node
     * @return 返回的是一个数组，node[0]就是未平衡结点，node[1]是node[0]的孩子节点,node[2]是node[3]的孩子节点
     * 这样做是为了还原未平衡节点与插入节点之间的路径，方便后面的旋转
     */
    private Node[] getFirstUnbalanceNode(Node node) {
        Node g, p, s;
        if (node != null && node.parent != null && node.parent.parent != null) {
            s = node;
            p = s.parent;
            g = p.parent;
            if (Math.abs(this.getHeight(g.lchild) - this.getHeight(g.rchild)) > 1) {
                return new Node[]{g, p, s};
            } else {
                return getFirstUnbalanceNode(s.parent);
            }
        }
        return null;
    }

    private void reBalance(Node[] unBalance) {
        if (unBalance == null || unBalance.length != 3) {
            return;
        }
        Node g = unBalance[0];
        Node p = unBalance[1];
        Node s = unBalance[2];

        if (MyBinarySearchTree.isLchild(p) && MyBinarySearchTree.isLchild(s)) {//左左型
            this.rightRevolve(g, p);
        } else if (MyBinarySearchTree.isRchild(p) && MyBinarySearchTree.isRchild(s)) {//右右型
            this.leftResolve(g, p);
        } else if (MyBinarySearchTree.isLchild(p)) {//左右型
            this.leftResolve(p, s);
            this.rightRevolve(g, s);
        } else {//右左型
            this.rightRevolve(p, s);
            this.leftResolve(g, s);
        }
    }

    /**
     * 以center结点位置为中心右旋，旋转后，原先的child作为中心结点，原先的中心结点作为child右孩子
     *
     * @param center 旋转的中心节点
     * @param child  中心节点的左孩子
     */
    private void rightRevolve(Node center, Node child) {
        if (center == null) {
            return;
        }
        if (child == null) {
            return;
        }
        Node parent = center.parent;
        if (parent == null) {//证明此时旋转的中心结点是root
            root = child;
            child.parent = null;
            Node rchild = child.rchild;
            child.rchild = center;
            center.parent = child;
            center.lchild = rchild;
            if(rchild !=null){
                rchild.parent = center;
            }
        } else {
            if (MyBinarySearchTree.isRchild(center)) {//中心结点是父节点的右孩子
                parent.rchild = child;
            } else {
                parent.lchild = child;
            }
            child.parent = parent;
            Node rchild = child.rchild;//需要将旋转前child的右孩子放到旋转后center的左节点中
            child.rchild = center;
            center.parent = child;
            center.lchild = rchild;
            if(rchild !=null){
                rchild.parent = center;
            }
        }

    }

    /**
     * 以center结点位置为中心左旋，旋转后，原先的child作为中心结点，原先的中心结点作为child左孩子
     *
     * @param center 旋转的中心节点
     * @param child  中心节点的右孩子
     */
    private void leftResolve(Node center, Node child) {
        if (center == null) {
            return;
        }
        if (child == null) {
            return;
        }
        Node parent = center.parent;
        if (parent == null) {//证明此时旋转的中心结点是root
            root = child;
            child.parent = null;
            Node lchild = child.lchild;
            child.lchild = center;
            center.parent = child;
            center.rchild = lchild;
            if(lchild!=null) {
                lchild.parent = center;
            }
        } else {
            if (MyBinarySearchTree.isRchild(center)) {//中心结点是父节点的右孩子
                parent.rchild = child;
            } else {
                parent.lchild = child;
            }
            child.parent = parent;
            Node lchild = child.lchild;//需要将旋转前child的右孩子放到旋转后center的左节点中
            child.lchild = center;
            center.parent = child;
            center.rchild = lchild;
            if(lchild!=null) {
                lchild.parent = center;
            }
        }
    }

}

各位大佬，原创不易呀，路过的点个赞！！！文章有错误欢迎大佬指正！！