代码随想录算法训练营第二十九天| 491.递增子序列 46.全排列 47.全排列 II

 

491.递增子序列

卡哥建议：本题和大家刚做过的 90.子集II 非常像，但又很不一样，很容易掉坑里。

 https://programmercarl.com/0491.%E9%80%92%E5%A2%9E%E5%AD%90%E5%BA%8F%E5%88%97.html

视频讲解：https://www.bilibili.com/video/BV1EG4y1h78v

做题思路：

在90.子集II中我们是通过排序，再加一个标记数组来达到去重的目的。

而本题求自增子序列，是不能对原数组进行排序的，排完序的数组都是自增子序列了。所以不能使用之前的去重逻辑！

用[4, 7, 6, 7]这个数组来举例，抽象为树形结构如图：

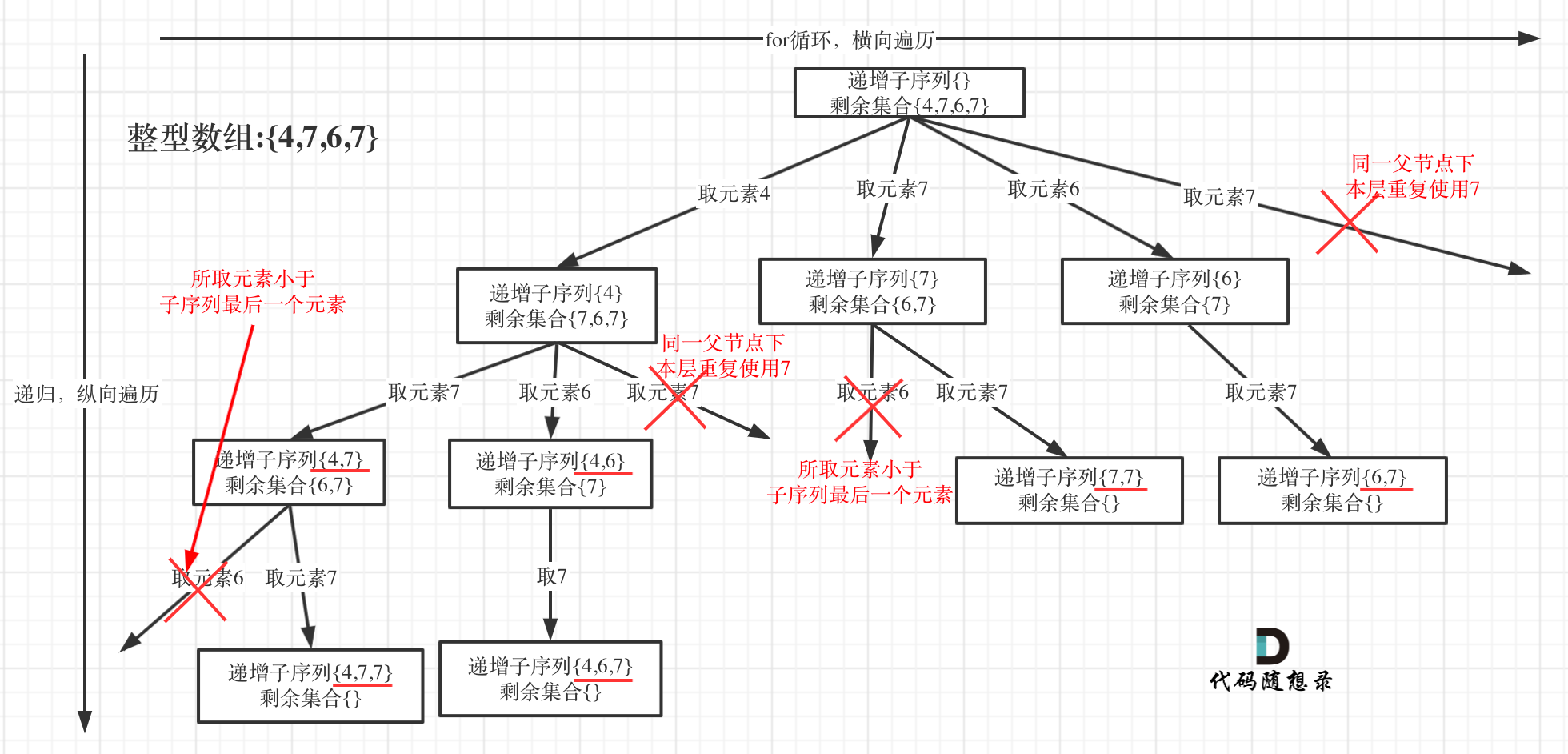
还得有树层去重，如上图的同一父节点不能重复使用7，同一父节点下的同层上使用过的元素就不能再使用了 

 关于uset，是记录本层元素是否重复使用，详细的看卡哥视频吧

本题代码：

 1 class Solution {
 2 private:
 3     vector<vector<int>> result;
 4     vector<int> path;
 5     void backtracking(vector<int>& nums, int startIndex) {
 6         if (path.size() > 1) {
 7             result.push_back(path);
 8         }
 9         int used[201] = {0}; // 这里使用数组来进行去重操作，题目说数值范围[-100, 100]
10         for (int i = startIndex; i < nums.size(); i++) {
11             if ((!path.empty() && nums[i] < path.back())
12                     || used[nums[i] + 100] == 1) {
13                     continue;
14             }
15             used[nums[i] + 100] = 1; // 记录这个元素在本层用过了，本层后面不能再用了
16             path.push_back(nums[i]);
17             backtracking(nums, i + 1);
18             path.pop_back();
19         }
20     }
21 public:
22     vector<vector<int>> findSubsequences(vector<int>& nums) {
23         result.clear();
24         path.clear();
25         backtracking(nums, 0);
26         return result;
27     }
28 };

46.全排列

卡哥建议：本题重点感受一下，排列问题 与 组合问题，组合总和，子集问题的区别。 为什么排列问题不用 startIndex

 https://programmercarl.com/0046.%E5%85%A8%E6%8E%92%E5%88%97.html

视频讲解：https://www.bilibili.com/video/BV19v4y1S79W

做题思路：

以[1,2,3]为例，抽象成树形结构如下：

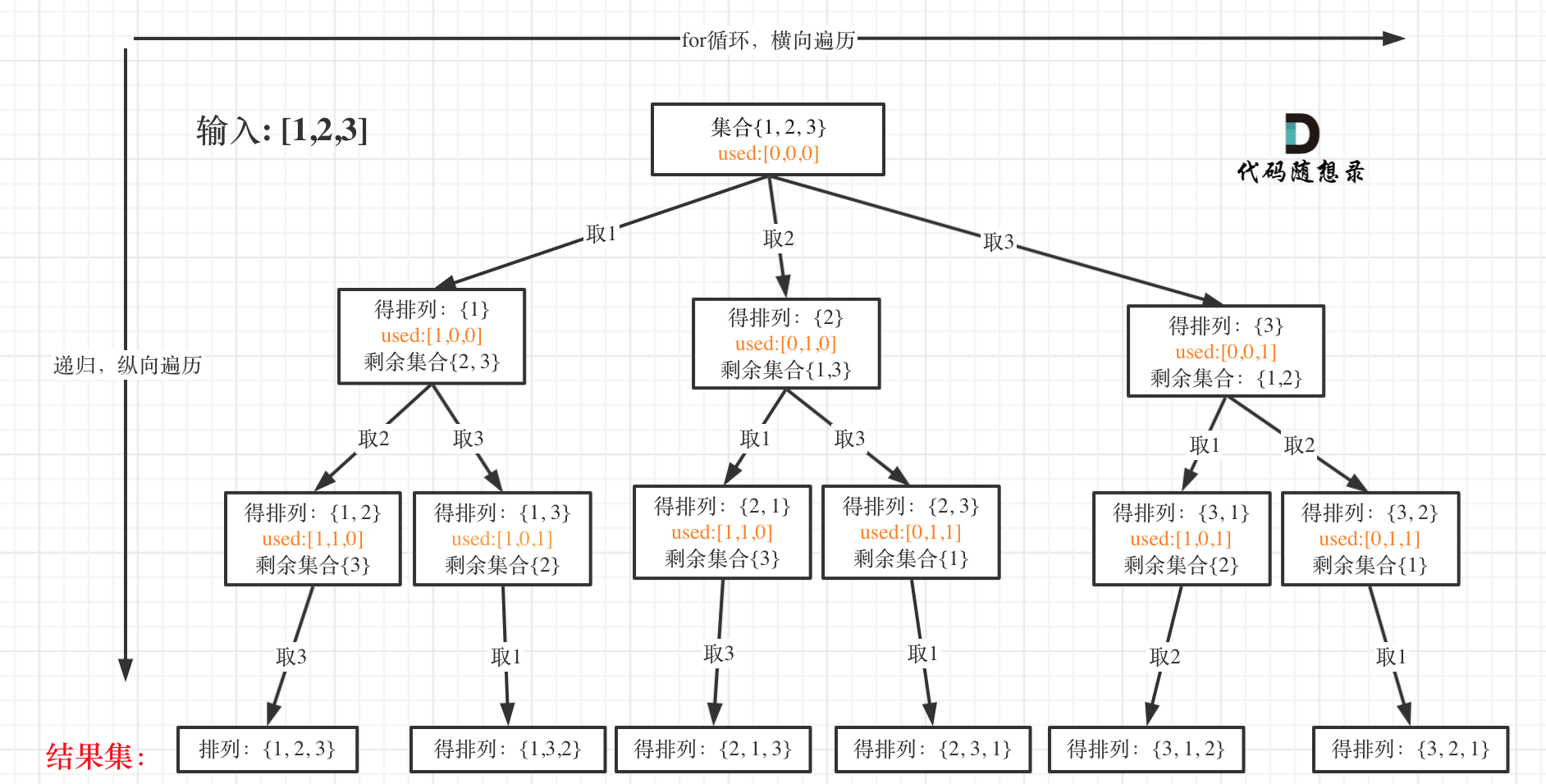
首先排列是有序的，也就是说 [1,2] 和 [2,1] 是两个集合，这和之前分析的子集以及组合所不同的地方。

可以看出元素1在[1,2]中已经使用过了，但是在[2,1]中还要在使用一次1，所以处理排列问题就不用使用startIndex了。

但排列问题需要一个used数组，其实就是记录此时path里都有哪些元素使用了，一个排列里一个元素只能使用一次。如图橘黄色部分所示。

可以看出叶子节点，就是收割结果的地方。那么什么时候，算是到达叶子节点呢？

当收集元素的数组path的大小达到和nums数组一样大的时候，说明找到了一个全排列，也表示到达了叶子节点。

本题代码：

 1 class Solution {
 2 public:
 3     vector<vector<int>> result;
 4     vector<int> path;
 5     void backtracking (vector<int>& nums, vector<bool>& used) {
 6         // 此时说明找到了一组
 7         if (path.size() == nums.size()) {
 8             result.push_back(path);
 9             return;
10         }
11         for (int i = 0; i < nums.size(); i++) {
12             if (used[i] == true) continue; // path里已经收录的元素，直接跳过
13             used[i] = true;
14             path.push_back(nums[i]);
15             backtracking(nums, used);
16             path.pop_back();
17             used[i] = false;
18         }
19     }
20     vector<vector<int>> permute(vector<int>& nums) {
21         result.clear();
22         path.clear();
23         vector<bool> used(nums.size(), false);
24         backtracking(nums, used);
25         return result;
26     }
27 };

47.全排列 II

卡哥建议：本题 就是我们讲过的 40.组合总和II 去重逻辑 和 46.全排列 的结合，可以先自己做一下，然后重点看一下 文章中 我讲的拓展内容。 used[i - 1] == true 也行，used[i - 1] == false 也行

 https://programmercarl.com/0047.%E5%85%A8%E6%8E%92%E5%88%97II.html

视频讲解：https://www.bilibili.com/video/BV1R84y1i7Tm

做题思路：

这道题目和46.全排列的区别在与给定一个可包含重复数字的序列，要返回所有不重复的全排列。

这里又涉及到去重了。

    还要强调的是去重一定要对元素进行排序，这样我们才方便通过相邻的节点来判断是否重复使用了。

以示例中的 [1,1,2]为例 （为了方便举例，已经排序）抽象为一棵树，去重过程如图：

图中我们对同一树层，前一位（也就是nums[i-1]）如果使用过，那么就进行去重。

    一般来说：组合问题和排列问题是在树形结构的叶子节点上收集结果，而子集问题就是取树上所有节点的结果。

    对于排列问题，树层上去重和树枝上去重，都是可以的，但是树层上去重效率更高！看卡哥文章解释。

本题代码：

 1 class Solution {
 2 private:
 3     vector<vector<int>> result;
 4     vector<int> path;
 5     void backtracking (vector<int>& nums, vector<bool>& used) {
 6         // 此时说明找到了一组
 7         if (path.size() == nums.size()) {
 8             result.push_back(path);
 9             return;
10         }
11         for (int i = 0; i < nums.size(); i++) {
12             // used[i - 1] == true，说明同一树枝nums[i - 1]使用过
13             // used[i - 1] == false，说明同一树层nums[i - 1]使用过
14             // 如果同一树层nums[i - 1]使用过则直接跳过
15             if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {
16                 continue;
17             }
18             if (used[i] == false) {
19                 used[i] = true;
20                 path.push_back(nums[i]);
21                 backtracking(nums, used);
22                 path.pop_back();
23                 used[i] = false;
24             }
25         }
26     }
27 public:
28     vector<vector<int>> permuteUnique(vector<int>& nums) {
29         result.clear();
30         path.clear();
31         sort(nums.begin(), nums.end()); // 排序
32         vector<bool> used(nums.size(), false);
33         backtracking(nums, used);
34         return result;
35     }
36 };