Codeforces Global Round 14 E. Phoenix and Computers

题目链接

点我跳转

题目大意

给定 \(N\) 台电脑，起初每台电脑都是关闭的

现在你可以随意打开电脑，但如果第 \(i-1\)、第 \(i+1\) 台电脑是开启的，则第 \(i\) 台电脑也会自动开启，而你无法手动开启它

问你有多少种打开电脑的方法，使得最后所有电脑都是开着的

解题思路

分成两步来解决.

第一步：

考虑：如果 \(N\) 台电脑我都要手动开启，有多少种方法？

可以枚举是从哪台电脑开始打开：

• 从 \(1\) 开始，剩下的 \(N-1\) 必须按照 \(2,3,...,n\) 的顺序开(不理解可以画一下)
• 从 \(2\) 开始，对于 \(2\) 左边的电脑 \([3\)~\(N]\)，\(4\) 必须在 \(3\) 开了之后开，\(5\) 必须在 \(4\) 开了之后开 \(...\) ，而 \(1\) 可以在任意时刻开机
• \(...\)
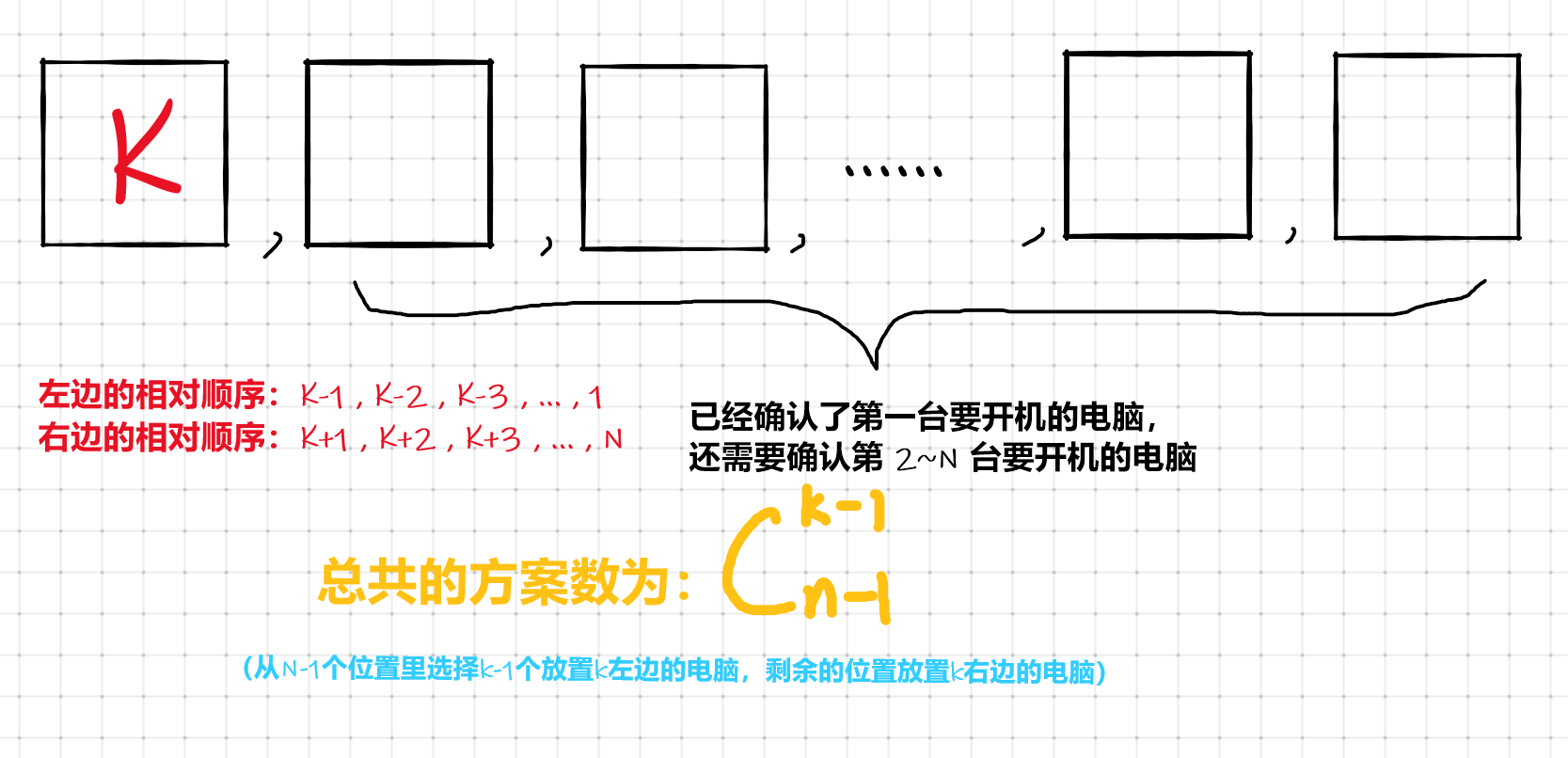
• 从 \(k\) 开始开，对于 \(k\) 左边的电脑， 它们的相对开机顺序必须是 \(k + 1 , k + 2 , ... , n\)
  
  对于\(k\) 右边的电脑，它们的相对开机顺序必须是 \(k-1,k-2,...,1\)
  
  不过左右两边的开机顺序是可以穿插在一起的
  
  

所以手动开启 \(N\) 台电脑的方案数为 \(C_{n-1}^{1}+C_{n-1}^{2}+\ldots +C_{n-1}^{n-1} = 2^{n-1}\)

第二步：

考虑：最后电脑开启的状态？

显然最后电脑开启的状态会是这样的：

手动开启 \(1\sim X_1\) → 自动开启 \(X_1+1\) → 手动开启 \(X_1+2\sim X2\) 台 →自动开启 \(X_2+1\) → \(...\) → 手动开启 \(X_{n-1} + 1\sim X_n\) ，其中需要保证 \(X_i + 1 < N\)

于是我们可以定义 \(f[i][j]\) 表示：前 \(i\) 台电脑，手动打开 \(j\) 台, 第 \(i\) 台是手动打开 ,

第 \(i + 1\) 台是自动打开的方案数

那么 \(f[i][j]\) → \(f[i + 1 + K][j + X_i]\) 的意义为：

手动打开 \(pos \sim i\) → 自动打开\(i+1\) → 手动打开 \(i + 2 \sim X_i\) 的过程

• \(f[i+1+X_i][j+X_i]\) 相对 \(f[i][j]\) 又多手动开启了 \(X_i\) 台电脑
• 这 \(X_i\) 台的电脑的开启方案数有 \(2^{Xi-1}\)种（第一步得出的结论）
• 然后考虑将这 \(X_i\) 台"新"电脑开机的顺序和 \(j\) 台"旧"电脑开机的顺序合并。
  
  即现在有 \(X_i+j\) 个开机顺序需要确认，我们可以从中选 \(X_i\) 个放"新"电脑的开机顺序，剩下的放"旧"电脑的开机顺序，那么方案数为 \(C_{X_i+j}^{X_i}\) (或者 \(C_{X_i+j}^{j}\)也可以）

所以可得： \(f[i + 1 + X_i][j + X_i] = f[i][j] \times 2^{Xi-1} \times C[j + X_i][X_i]\)

答案即： $ans=\sum ^{n}_{i=0}f\left[ n\right] \left[ i\right] $

\(i\)、\(j\)、\(X_i\) 都可以通过枚举得到

写题解不易，如有帮助到您请点个赞给予我一点小小的鼓励！

AC_Code

#include<bits/stdc++.h>
using namespace std;
const int N = 4e2 + 10;
long long C[N][N] , bit[N];
long long n , m , ans , f[N][N];
void init(int mod)
{
	bit[0] = 1;
	for(int i = 1 ; i <= N - 10 ; i ++) bit[i] = bit[i - 1] * 2 % mod;
	for(int i = 0 ; i <= N - 10 ; i ++)
	{
		C[i][0] = 1;
		for(int j = 1 ; j <= i ; j ++) C[i][j] = (C[i - 1][j - 1] + C[i - 1][j]) % mod;
	}
}
signed main()
{
	cin >> n >> m;
	init(m);
	for(int i = 1 ; i <= n ; i ++)
	{
		f[i][i] = bit[i - 1];
		for(int j = 0 ; j <= i ; j ++)
		{
			for(int k = 1 ; k + i + 1 <= n; k ++)
			{
				f[i + 1 + k][j + k] += f[i][j] * bit[k - 1] % m * C[j + k][k] % m;
				f[i + 1 + k][j + k] %= m;
			}
		}
	}
	for(int i = 0 ; i <= n ; i ++) ans += f[n][i] , ans %= m;
	cout << ans << '\n';
	return 0;
}