【OI】蛇形填数题的深入探究

题目：在 n×n 方阵里填入 1,2,...n×n, 要求蛇形填数。例如，n=4 时方阵为：

　　　　10  11  12  1

　　　　9    16  13  2

　　　　8    15  14  3

　　　　7     6    5   4

空格不严格要求输出，其中（n<=8）。

解：

 1 #include <stdio.h>
 2 #include <string.h>
 3
 4 #define maxn 20
 5 int a[maxn][maxn];
 6
 7 int main ()
 8 {
 9     int n , x , y , tot = 0;
10     scanf("%d",&n);
11     memset(a,0,sizeof(a));
12     tot = a[x = 0][y = n-1] = 1;
13
14     while (tot < n*n)
15     {
16         while (x+1<n && !a[x+1][y])    a[++x][y] = ++tot;
17         while (y-1>=0 && !a[x][y-1]) a[x][--y] = ++ tot;
18         while (x-1>=0 && !a[x-1][y]) a[--x][y] = ++tot;
19         while (y+1<n && !a[x][y+1])    a[x][++y] = ++tot;
20
21     }
22
23     for (x = 0;x < n;x++)
24     {
25         for (y = 0;y < n;y++)
26         {
27             printf("%3d",a[x][y]);　　//输出和例题一样的格式
28         }
29         printf("\n");
30     }
31
32     return 0;
33 }

下面对一些细节进行探究：

　　一、二维数组的数学抽象

　　　　由于我们无法控制鼠标的位置，我们只能通过平面的坐标系来定位每一个数的位置，在顺次输出几个。这就涉及到了平面坐标系在C语言中的抽象，很显然的，我们使用二维数组。

　　　

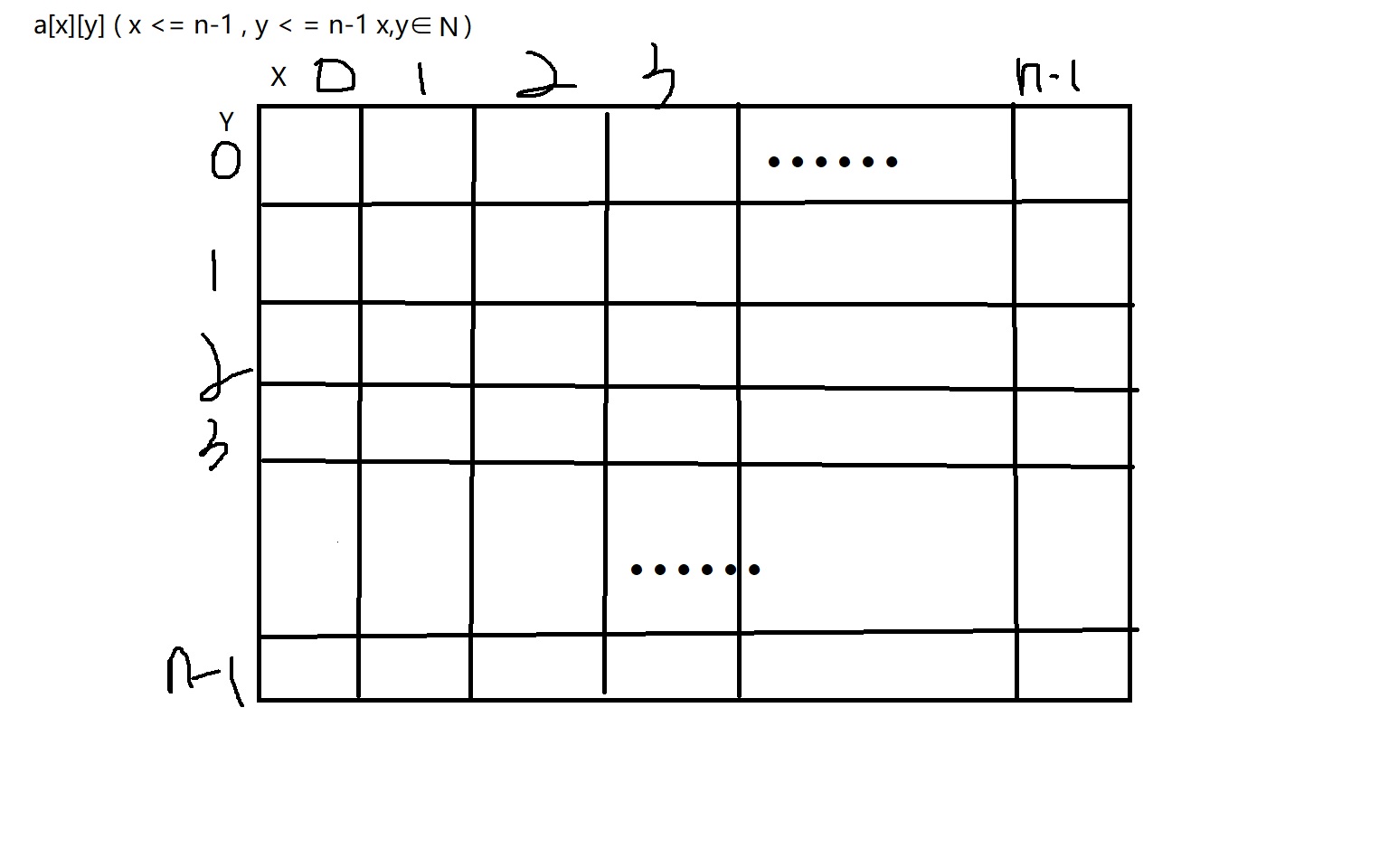
　　　　每一个格子就是一个坐标，这样抽象的好处是我们无需考虑其如何输出，只需要考虑我们如何赋值即可。

　　　　另外的一个技巧是：将整个数组初始化为0，这样0就代表是该坐标位置未被占去的状态，可以用!a[x][y}是否为1来判断。并且，无论格子内填了什么，!a[x][y]的值都会是0。

　　二、简化运算符的使用

　　　　就像书上说的一样，

　　　　tot = a[x = 0][y = n-1] = 1;

　　　　这句话包含了很大的信息量。不仅使得代码变得简洁，而且没有使程序的易读性丧失。

　　三、短路运算符的妙用

　　　　当你不能避免某一条语句会导致下标溢出的时候，使用短路运算符可以很好的解决问题。就比如将!a[x+1][y]放入&&的后面，即使x+1>=n也不会使得下标溢出。

　　四、细节问题

　　　　注意观察变量的情况。如果tot的初始值为1，那么下面的句子就要使用tot++。

来自：《算法竞赛入门经典》--紫皮书