C++ 矩形交集和并集的面积-离散化

//离散化，x,y坐标分别按从小到大排序
//离散化
//1、首先分离出所有的横坐标和纵坐标分别按升序存入数组X[ ]和Y[ ]中.
//2、 设数组XY[ ][ ].对于每个矩形(x1,y1)(x2,y2)确定i1,i2,j1,j2,使得,X[i1]>x1,X[i2]<=x2,Y[i1]>y1,Y[i2]>=y2令XY[ i ][ j ] = 1 (i从i1到i2，j从j1到j2)
//3、统计面积：area+=XY[i][j] *(X[i]-X[i-1])*(Y[i] – Y[i-1])
 
#include<iostream>
#include<string.h>
#include<stdio.h>
#include <algorithm>
using namespace std;
double x[201],y[201],s[101][4];
int xy[201][201] = {0};
int n,cas=0;
double sum1; // 并集面积
double sum2; // 交集面积
int main()
{
    int i,j,k;
    while(cin>>n)
    {
        if(n==0)
            break;
        cas++;
        k=0;
        sum1 = 0.0;
        sum2 = 0.0;
        memset(xy,0,sizeof(xy));
        for(i=1;i<=n;i++)
        {
            cin>>s[i][0]>>s[i][1]>>s[i][2]>>s[i][3];
            x[k]=s[i][0];
            y[k]=s[i][1];
            k++;
            x[k]=s[i][2];
            y[k]=s[i][3];
            k++;
        }
        sort(x,x+2*n);
        sort(y,y+2*n);
        int kk = 0;
        for(k=1;k<=n;k++)
        {
            int i1,i2,j1,j2;
            for(i1=0;i1<2*n;i1++)
            {
                if(x[i1]==s[k][0])
                    break;
            }
            for(i2=0;i2<2*n;i2++)
            {
                if(x[i2]==s[k][2])
                    break;
            }
            for(j1=0;j1<2*n;j1++)
            {
                if(y[j1]==s[k][1])
                    break;
            }
            for(j2=0;j2<2*n;j2++)
            {
                if(y[j2]==s[k][3])
                    break;
            }
            for(i=i1;i<i2;i++)
            {
                for(j=j1;j<j2;j++)
                {
                    xy[i][j] |= 1<<(k-1);
                }
            }
            kk |= 1<<(k-1); // 所有bit都置为1
        }
 
        for(i=0;i<2*n;i++)
        {
            for(j=0;j<2*n;j++)
            {
                sum1 += ((xy[i][j] != 0 ? 1:0)*(x[i+1]-x[i])*(y[j+1]-y[j])); // 只要!=0，说明至少有一个矩形占据过
                sum2 += ((xy[i][j] == kk ? 1:0)*(x[i+1]-x[i])*(y[j+1]-y[j])); // 每个矩形都占据过这里
            }
        }
        printf("Test case #%d\n",cas);
        printf("并集面积: %.2f\n",sum1);
        printf("交集面积: %.2f\n",sum2);
        printf("\n");
    }
    return 0;
}

输入：

2
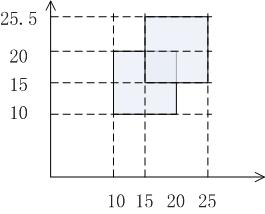
10 10 20 20
15 15 25 25.5

输出：

Test case #1
并集面积: 180.00
交集面积: 25.00

输入：
3
10 10 20 20
15 8 30 15
17 13 25 25

输出：

Test case #2
并集面积: 245.00
交集面积: 6.00

转自：https://blog.csdn.net/fall221/article/details/12314489?locationNum=10&fps=1