DFT、DTFT、DFS、FFT之间的关系

DFT、DTFT、DFS、FFT、FT、FS之间的关系

FT和FS是研究连续信号的，在数字信号处理中不涉及。

主要是前四种的关系：

• DFT（Discrete Fourier Transform）：离散傅里叶变换

• DTFT（Discrete-time Fourier Transform）：离散时间傅里叶变换

• DFS（Discrete Fourier Series）：离散傅里叶级数

• FFT（Fast Fourier Transform）：快速傅里叶变换

首先来说图（1）和图（2），对于一个模拟信号，如图(1)所示，要分析它的频率成分，必须变换到频域，这是通过傅立叶变换即FT(Fourier Transform)得到的，于是有了模拟信号的频谱，如图(2)；注意1：时域和频域都是连续的！

但是，计算机只能处理数字信号，首先需要将原模拟信号在时域离散化，即在时域对其进行采样，采样脉冲序列如图(3)所示，该采样序列的频谱如图(4)，可见它的频谱也是一系列的脉冲。所谓时域采样，就是在时域对信号进行相乘，(1)×(3)后可以得到离散时间信号x[n]，如图(5)所示；由前面的性质1，时域的相乘相当于频域的卷积，那么，图(2)与图(4)进行卷积，根据前面的性质2知，**会在各个脉冲点处出现镜像，于是得到图(6)，它就是图(5)所示离散时间信号x[n]的DTFT(Discrete time Fourier Transform)，即离散时间傅立叶变换，这里强调的是“离散时间”四个字。**注意2：此时时域是离散的，而频域依然是连续的。

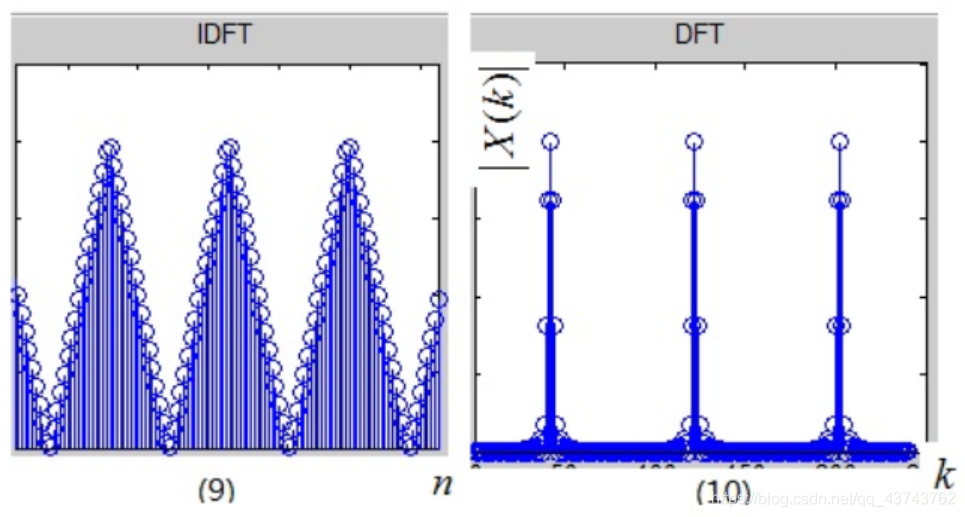
经过上面两个步骤，我们得到的信号依然不能被计算机处理，因为频域既连续，又周期。我们自然就想到，既然时域可以采样，为什么频域不能采样呢？这样不就时域与频域都离散化了吗？没错，接下来对频域在进行采样，频域采样信号的频谱如图(8)所示，它的时域波形如图(7)。现在我们进行频域采样，即频域相乘，图(6)×图(8)得到图(10)，那么根据性质1，这次是频域相乘，时域卷积了吧，图(5)和图(7)卷积得到图(9)，不出所料的，镜像会呈周期性出现在各个脉冲点处。我们取图（10）周期序列的主值区间，并记为X(k)，它就是序列x[n]的DFT(Discrete Fourier Transform)，即离散傅立叶变换。可见，DFT只是为了计算机处理方便，在频率域对DTFT进行的采样并截取主值而已。有人可能疑惑，对图(10)进行IDFT，回到时域即图(9)，它与原离散信号图(5)所示的x[n]不同呀，它是x[n]的周期性延拓！没错，因此你去查找一个IDFT的定义式，是不是对n的取值区间进行限制了呢？这一限制的含义就是，取该周期延拓序列的主值区间，即可还原x[n]！

FFT呢？FFT的提出完全是为了快速计算DFT而已，它的本质就是DFT！我们常用的信号处理软件MATLAB或者DSP软件包中，包含的算法都是FFT而非DFT。

DFS,是针对时域周期信号提出的，如果对图(9）所示周期延拓信号进行DFS，就会得到图(10)，只要截取其主值区间，则与DFT是完全的一一对应的精确关系。这点对照DFS和DFT的定义式也可以轻易的看出。因此DFS与DFT的本质是一样的，只不过描述的方法不同而已。

我理解的就是：

DTFT（离散时间傅里叶变换，强调的是离散时间，只保证时域是离散的）得到对时域连续信号的离散化采样后的频谱函数，这个采样后时域的信号是离散的（采样序列是离散的），但是由于采样信号在频域的周期性，而且根据时域相乘、频域卷积的原则，原信号的频谱（是连续的）会搬移在采样信号的每一个脉冲点，这样一来，DTFT得到的频谱函数就是连续且周期的！DTFT就是对时域的采样！

但是，连续且周期的频谱信号不能够被计算机所处理，所以要就要对频域信号进行采样了（DFT）！

与时域采样相同，频域采样也是一系列的周期序列信号相乘，这样，频域的信号就是离散的了，但此时频域信号仍然是周期的。一旦对频域进行采样后（频域相乘、时域卷积），时域又和周期脉冲信号卷积了，结果就是DTFT求出的时域离散信号被搬移到每一个脉冲所在处了，但这样就实现了时域和频域的离散化！DFT就是对DTFT后的频域信号再进行一次离散化采样，得到了离散周期的时域、频域信号！（DFT会对得到的周期性频谱截取主值）

此时，时域是离散的，但是有周期性，计算机不好处理！

通过DFS截取时域离散周期信号的主值！

DTDF是数学家的杰作、DFT是工程师的杰作！离散化有助于计算机分析！

综上所述，要将模拟信号转化为可以计算机处理的离散信号，经过一下几步：

1.DTFT对时域离散化采样

2.DFT对频域离散化采样（顺便截取频域周期信号主值）

3.DFS截取时域周期信号主值

4.这样，就将连续信号转化为离散信号了（时域、频域都离散）

文章参考：参考链接