二叉搜索树、平衡二叉树、红黑树、B树、B+树

完全二叉树：

空树不是完全二叉树，叶子结点只能出现在最下层和次下层，且最下层的叶子结点集中在树的左部。如果遇到一个结点，左孩子不为空，右孩子为空；或者左右孩子都为空；则该节点之后的队列中的结点都为叶子节点；该树才是完全二叉树，否则就不是完全二叉树；

具有n个节点的完全二叉树深为log2x+1（其中x表示不大于n的最大整数）

满二叉树：

除最后一层无任何子节点外，每一层上的所有结点都有两个子结点的二叉树。

 二叉搜索树（二叉排序树、又称二叉查找树）：

可以为空树，或者是具备如下性质：若它的左子树不空，则左子树上的所有结点的值均小于根节点的值；若它的右子树不空，则右子树上的所有结点的值均大于根节点的值，左右子树分别为二叉排序树。

理论上说，二叉搜索树的查询、插入、和删除一个节点的时间复杂度均为O(log(n))

但是还有一种特殊情况：

这种情况下，二叉搜索树已经变更为链表，搜索一个元素的时间复杂度也变成了O(n)

出现这种情况的原因是二叉搜索树没有自平衡的机制，所以就有了平衡二叉树。

平衡二叉树（是一种概念，它有几种实现方式：红黑树、AVL树）

它是一个空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是平衡二叉树

当AVL树插入一个节点时，如果平衡因子已经大于1了，这个时候就要进行左旋、右旋使之平衡因子恢复为1

红黑树

红黑树是一种平衡二叉查找树的变体，它的左右子树高差有可能大于 1，所以红黑树不是严格意义上的平衡二叉树（AVL），但 对之进行平衡的代价较低， 其平均统计性能要强于 AVL 。

红黑树和AVL树的区别：

RB-Tree和AVL树作为BBST，其实现的算法时间复杂度相同，AVL作为最先提出的BBST，貌似RB-tree实现的功能都可以用AVL树是代替，那么为什么还需要引入RB-Tree呢？

1. 红黑树不追求"完全平衡"，即不像AVL那样要求节点的 |balFact| <= 1，它只要求部分达到平衡，但是提出了为节点增加颜色，红黑是用非严格的平衡来换取增删节点时候旋转次数的降低，任何不平衡都会在三次旋转之内解决，而AVL是严格平衡树，因此在增加或者删除节点的时候，根据不同情况，旋转的次数比红黑树要多。
2. 就插入节点导致树失衡的情况，AVL和RB-Tree都是最多两次树旋转来实现复衡rebalance，旋转的量级是O(1)
   
   删除节点导致失衡，AVL需要维护从被删除节点到根节点root这条路径上所有节点的平衡，旋转的量级为O(logN)，而RB-Tree最多只需要旋转3次实现复衡，只需O(1)，所以说RB-Tree删除节点的rebalance的效率更高，开销更小！
3. AVL的结构相较于RB-Tree更为平衡，插入和删除引起失衡，如2所述，RB-Tree复衡效率更高；当然，由于AVL高度平衡，因此AVL的Search效率更高啦。
4. 针对插入和删除节点导致失衡后的rebalance操作，红黑树能够提供一个比较"便宜"的解决方案，降低开销，是对search，insert ，以及delete效率的折衷，总体来说，RB-Tree的统计性能高于AVL.
5. 故引入RB-Tree是功能、性能、空间开销的折中结果。
   
   5.1 AVL更平衡，结构上更加直观，时间效能针对读取而言更高；维护稍慢，空间开销较大。
   
   5.2 红黑树，读取略逊于AVL，维护强于AVL，空间开销与AVL类似，内容极多时略优于AVL，维护优于AVL。

总结：实际应用中，若搜索的次数远远大于插入和删除，那么选择AVL，如果搜索，插入删除次数几乎差不多，应该选择RB-Tree。

红黑树是一种含有红黑结点并能自平衡的二叉查找树。它必须除了满足二叉搜索树的性质外，还要满足下面的性质：

性质1：每个节点要么是黑色，要么是红色。

性质2：根节点是黑色。
性质3：每个叶子节点（NIL）是黑色。
性质4：每个红色结点的两个子结点一定都是黑色。
性质5：任意一结点到每个叶子结点的路径都包含数量相同的黑结点。

我们知道Mysql Innodb存储引擎的索引的数据结构为B+树，那么什么是B+树呢？

先来了解下B树：

一种平衡的多叉树，称为B树（或B-树、B_树）

一棵m阶B树(balanced tree of order m)是一棵平衡的m路搜索树。它或者是空树，或者是满足下列性质的树：

1、根结点至少有两个子女；

2、每个非根节点所包含的关键字个数 j 满足：┌m/2┐ - 1 <= j <= m - 1；

3、除根结点以外的所有结点（不包括叶子结点）的度数正好是关键字总数加1，故内部子树个数 k 满足：┌m/2┐ <= k <= m ；

4、所有的叶子结点都位于同一层。

简单理解为：平衡多叉树为B树（每一个子节点上都是有数据的），叶子节点之间无指针相邻

 

什么是B+树呢？

B+树是B树的一种变形形式，B+树上的叶子结点存储关键字以及相应记录的地址，叶子结点以上各层作为索引使用。一棵m阶的B+树定义如下

(1)每个结点至多有m个子女；

(2)除根结点外，每个结点至少有[m/2]个子女，根结点至少有两个子女；

(3)有k个子女的结点必有k个关键字。

B+树的查找与B树不同，当索引部分某个结点的关键字与所查的关键字相等时，并不停止查找，应继续沿着这个关键字左边的指针向下，一直查到该关键字所在的叶子结点为止。

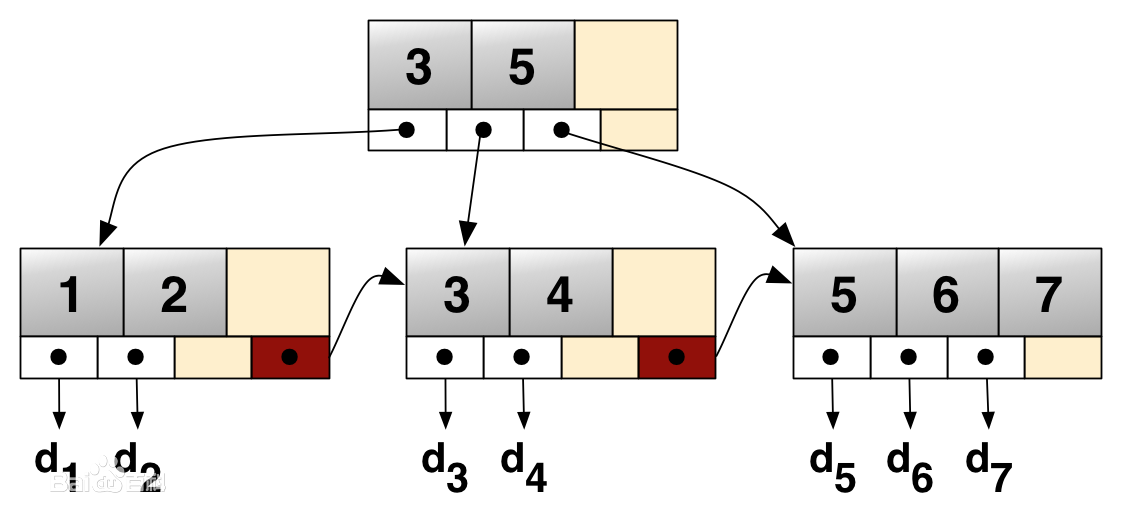
特点：

数据只出现在叶子节点

所有叶子节点增加了一个链指针

简单总结：mysql中的innodb为什么用B+树不使用B树

1.B树把数据放在了每个节点上，而B+树把数据放在了叶子节点上，所以单个查询速度B+平均要快于B树，但是B-树的每个节点都有data域（指针），这无疑增大了节点大小，说白了增加了磁盘IO次数（磁盘IO一次读出的数据量大小是固定的，单个数据变大，每次读出的就少，IO次数增多），而B+树除了叶子节点其它节点并不存储数据，节点小，磁盘IO次数就少。

2.另一方面，由于B+树有链指针，所以更方便区间查询。

https://www.jianshu.com/p/37436ed14cc6

https://mp.weixin.qq.com/s/9s6c1sPN7avqwxZC7BsVUQ