【数据结构与算法Python版学习笔记】图——最短路径问题、最小生成树

最短路径问题

概念

• 可以通过“traceroute”命令来跟踪信息传送的路径：
  
  traceroute www.lib.pku.edu.cn

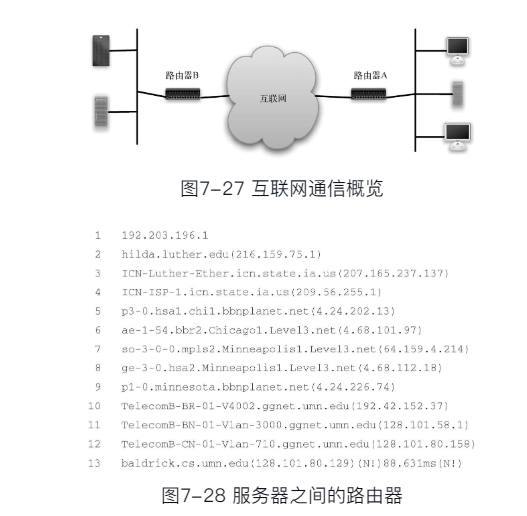
• 可以将互联网路由器体系表示为一个带权边的图
  • 路由器作为顶点，路由器之间网络连接作为边权重可以包括网络连接的速度、网络负载程度、分时段优先级等影响因素
  • 作为一个抽象，我们把所有影响因素合成为单一的权重
• 解决信息在路由器网络中选择传播速度最快路径的问题， 就转变为在带权图上最短路径的问题。
• 这个问题与广度优先搜索BFS算法解决的词梯问题相似， 只是在边上增加了权重
  
  如果所有权重相等，还是还原到词梯问题

Dijkstra算法

思路

Dijkstra算法可用于确定最短路径，它是一种循环算法，可以提供从一个顶点到其他所有顶点的最短路径。这与广度优先搜索非常像。

具体实现上，

• 在顶点Vertex类中的成员dist用于记录从开始顶点到本顶点的最短带权路径长度（权重之和） ， 算法对图中的每个顶点迭代一次
• 顶点的访问次序由一个优先队列来控制，队列中作为优先级的是顶点的dist属性。
• 最初， 只有开始顶点dist设为0， 而其他所有顶点dist设为sys.maxsize（最大整数） ， 全部加入优先队列。
• 随着队列中每个最低dist顶点率先出队
• 并计算它与邻接顶点的权重， 会引起其它顶点dist的减小和修改， 引起堆重排
• 并据更新后的dist优先级再依次出队

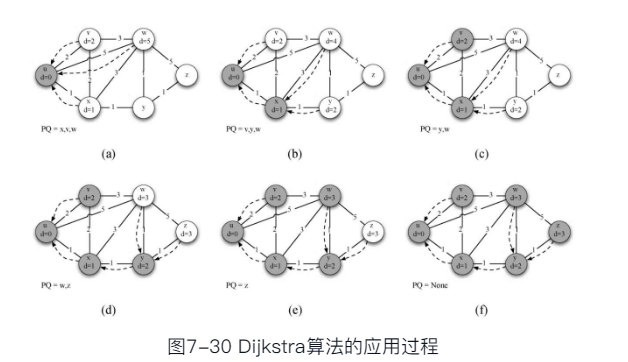
代码

def dijkstra(aGraph, start):
    pq = PriorityQueue()
    start.setDistance(0)
    # 对所有顶点建堆，形成优先队列
    pd.buildHeap([v.getDistance(), v for v in aGraph])
    while not pq.isEmpty():
        # 优先队列出队
        currentVert = pq.delMin()
        for nextVert in currentVert.getConnections():
            newDist = currentVert.getDistance()+currentVert.getWeight(nextVert)
            # 修改出队顶点所邻接顶点的dist,并逐个重排队列
            if newDist < nextVert.getDistance():
                nextVert.setDistance(newDist)
                nextVert.setPred(currentVert)
                pq.decreaseKey(nextVert, newDist)

算法分析

• 首先， 将所有顶点加入优先队列并建堆，时间复杂度为O(|V|)
• 其次， 每个顶点仅出队1次， 每次delMin花费O(log|V|)， 一共就是O(|V|log|V|)
• 另外， 每个边关联到的顶点会做一次decreaseKey操作（O(log|V|))， 一共是O(|E|log|V|)
• 上 面 三 个 加 在 一 起 ， 数 量 级 就 是O((|V|+|E|)log|V|)

小结

• 需要注意的是， Dijkstra算法只能处理大于0的权重
  
  如果图中出现负数权重，则算法会陷入无限循环

• 虽然Dijkstra算法完美解决了带权图的最短路径问题， 但实际上Internet的路由器中采用的是其它算法

• 其中最重要的原因是， Dijkstra算法需要具备整个图的数据， 但对于Internet的路由器来说， 显然无法将整个Internet所有路由器及其连接信息保存在本地

  • 这不仅是数据量的问题， Internet动态变化的特性也使得保存全图缺乏现实性。

• 路由器的选径算法（或“路由算法”） 对于互联网极其重要
  
  https://baike.baidu.com/item/距离向量路由算法

---

最小生成树 Prim算法

信息广播问题：单播解法

• 本算法涉及到在互联网中网游设计者和网络收音机所面临的问题：信息广播问题网游需要让所有玩家获知其他玩家所在的位置收音机则需要让所有听众获取直播的音频数据

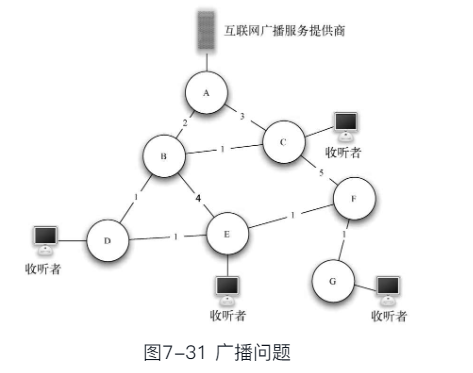
• 信息广播问题最简单的解法是由广播源维护一个收听者的列表， 将每条消息向每个

收听者发送一次。如图，每条消息会被发送4次，每个消息都采用最短路径算法到达收听者

• 路由器A会处理4次相同消息， C仅会处理1次；而B/D位于其它3个收听者的最短路径上， 则各会处理转发3次相同消息
• 会产生许多额外流量

信息广播问题：洪水解法

• 信息广播问题的暴力解法， 是将每条消息在路由器间散布出去
• 所有的路由器都将收到的消息转发到自己相邻的路由器和收听者
• 显然， 如果没有任何限制， 这个方法将造成网络洪水灾难
• 很多路由器和收听者会不断重复收到相同的消息， 永不停止！

优化

• 所以， 洪水解法一般会给每条消息附加一个生命值（TTL:Time To Live） ， 初始设置为从消息源到最远的收听者的距离；
• 每个路由器收到一条消息， 如果其TTL值大于0， 则将TTL减少1， 再转发出去如果TTL等于0了，则就直接抛弃这个消息。
• TTL的设置防止了灾难发生， 但这种洪水解法显然比前述的单播方法所产生的流量还要大。

信息广播问题：最小生成树

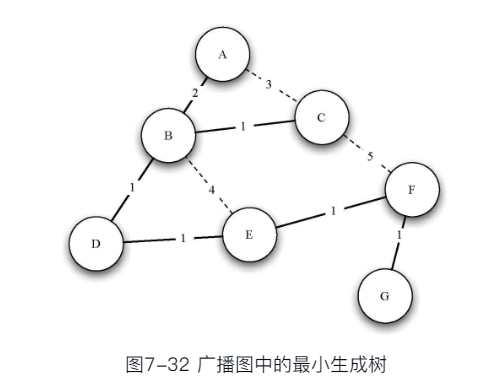
• 信息广播问题的最优解法， 依赖于路由器关系图上选取具有最小权重的生成树
  
  （minimum weight spanning tree）
  • 生成树：拥有图中所有的顶点和最少数量的边，以保持连通的子图。
• 图G(V,E)的最小生成树T， 定义为包含所有顶点V，以及E的无圈子集，并且边权重之和最小

这样信息广播就只需要从A开始， 沿着树的路径层次向下传播就可以达到每个路由器只需要处理1次消息，同时总费用最小

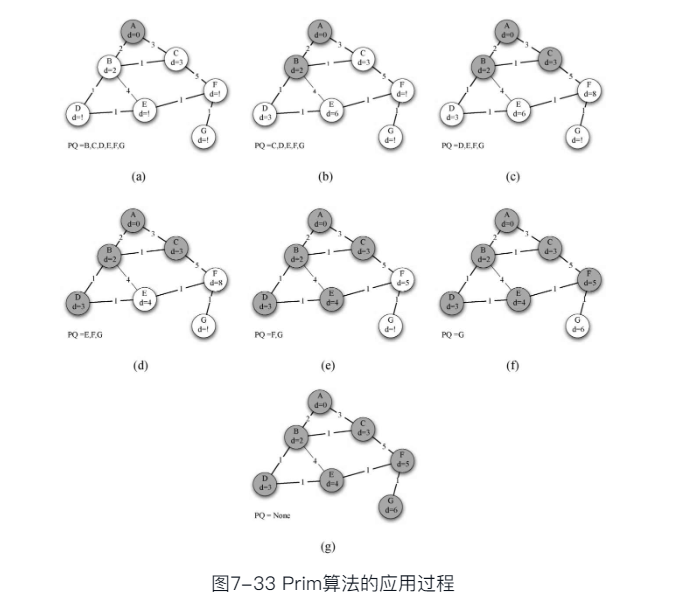
Prim算法

• 解决最小生成树问题的Prim算法， 属于“贪心算法”， 即每步都沿着最小权重的边向前搜索。
• 构造最小生成树的思路很简单， 如果T还不是生成树， 则反复做：
  
  找到一条最小权重的可以安全添加的边，将边添加到树T
• “可以安全添加”的边， 定义为一端顶点在树中， 另一端不在树中的边， 以便保持树的无圈特性

def prim(G, start):
    pq = PriorityQueue()
    for v in G:
        v.setDistance(sys.maxsize)
        v.setPred(None)
    start.setDistance(0)
    pd.buildHeap([(v.getDistance(), v) for v in G])
    while not pq.isEmpty():
        # 优先队列出队
        currentVert = pq.delMin()
        for nextVert in currentVert.getConnections():
            newCost = currentVert.getWeight(nextVert)
            # 修改出队顶点所邻接顶点的dist,并逐个重排队列
            if nextVert in pq and newCost < nextVert.getDistance():
                nextVert.setDistance(newCost)
                nextVert.setPred(currentVert)
                pq.decreaseKey(nextVert, newCost)