【LeetCode】1579. 保证图可完全遍历 Remove Max Number of Edges to Keep Graph Fully Traversable

• 作者： 负雪明烛
• id： fuxuemingzhu
• 个人博客：http://fuxuemingzhu.cn/

---

目录

• 题目描述
• 题目大意
• 解题思路
• • 并查集
• 代码
• 欢迎加入组织
• 日期

题目地址：https://leetcode-cn.com/problems/remove-max-number-of-edges-to-keep-graph-fully-traversable

题目描述

Alice 和 Bob 共有一个无向图，其中包含 n 个节点和 3 种类型的边：

类型 1：只能由 Alice 遍历。
类型 2：只能由 Bob 遍历。
类型 3：Alice 和 Bob 都可以遍历。

给你一个数组 edges ，其中 edges[i] = [typei, ui, vi] 表示节点 ui 和 vi 之间存在类型为 typei 的双向边。请你在保证图仍能够被 Alice 和 Bob 完全遍历的前提下，找出可以删除的最大边数。如果从任何节点开始，Alice 和 Bob 都可以到达所有其他节点，则认为图是可以完全遍历的。

返回可以删除的最大边数，如果 Alice 和 Bob 无法完全遍历图，则返回 -1 。

示例 1：

输入：n = 4, edges = [[3,1,2],[3,2,3],[1,1,3],[1,2,4],[1,1,2],[2,3,4]]
输出：2
解释：如果删除 [1,1,2] 和 [1,1,3] 这两条边，Alice 和 Bob 仍然可以完全遍历这个图。再删除任何其他的边都无法保证图可以完全遍历。所以可以删除的最大边数是 2 。

示例 2：

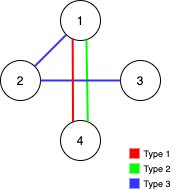
输入：n = 4, edges = [[3,1,2],[3,2,3],[1,1,4],[2,1,4]]
输出：0
解释：注意，删除任何一条边都会使 Alice 和 Bob 无法完全遍历这个图。

示例 3：

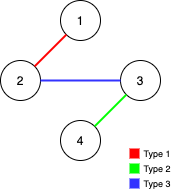
输入：n = 4, edges = [[3,2,3],[1,1,2],[2,3,4]]
输出：-1
解释：在当前图中，Alice 无法从其他节点到达节点 4 。类似地，Bob 也不能达到节点 1 。因此，图无法完全遍历。

提示：

1. 1 <= n <= 10^5
2. 1 <= edges.length <= min(10^5, 3 * n * (n-1) / 2)
3. edges[i].length == 3
4. 1 <= edges[i][0] <= 3
5. 1 <= edges[i][1] < edges[i][2] <= n
6. 所有元组 (typei, ui, vi) 互不相同

题目大意

删除最多的边，让两个人最终都能遍历全图。

解题思路

并查集

题目要求最多删除多少条边之后，两人都能完全遍历该图，换句话说，是要保证最终整个图对两个人都是连通的。

我们先讨论简单的情况，假设只有一种类型的边并且只有 1 个人，这种情况下最多删除图中的多少条边，仍然能让此人完全遍历这个图呢？

连通区域的问题，一般都可以使用 并查集 解决。并查集分为 “并” 与 “查” 两部分。“并” 的部分，表示让两个区域连通；“查” 的部分，表示检查两个区域是否连通。本文不详细讲解并查集，但是会在代码部分，分享一个常用的并查集的代码模板。

我们需要遍历每一条边，判断这条边的两个顶点所在区域是否连通（利用了并查集的“查”的功能）。如果两个区域已经连通，说明该边无效，则抛弃该边；否则，说明这条边连通了两个未连通的区域，需要保留该边，且连通这两个区域（利用了并查集的“并”的功能）。

由于本题有两人，所以需要对 Alice 和 Bob 两人分别建一个并查集。我们仍然需要遍历每一条边，由于每个边是有类型的，因此需要根据这条边类型，确定是使用 Alice 的并查集还是 Bob 的并查集。

• 类型 1：只能由 Alice 遍历，故使用 Alice 的并查集。
• 类型 2：只能由 Bob 遍历，故使用 Bob 的并查集。
• 类型 3：Alice 和 Bob 都可以遍历，故使用 Alice 和 Bob 两个人的并查集。

类型 3 的边可以同时连通 Alice 和 Bob 两个人的区域，一条边可以抵得上类型 1 和类型 2 两条边。题目要求最多可以删除多少条边，也就是说最终的图中应该保留最少的边，因此我们想到可以优先保留类型 3 的边。这种策略叫做“贪心”。

至此，本题的解题方法已经清楚了：

1. 对 Alice 和 Bob 两人分别建一个并查集；

2. 遍历所有类型 3 的边，分别检查 Alice 和 Bob 的两个并查集，判断此边的两个顶点所在区域是否连通，若不连通则使其连通；若已连通，则可以删除该边；

3. 遍历所有类型 1 和类型 2 的边，如果是类型 1 则检查 Alice 的并查集，如果是类型 2 则检查 Bob 的并查集，判断此边的两个顶点所在区域是否连通，若不连通则使其连通；若已连通，则可以删除该边。

4. 判断两个并查集的最终连通区域数是否都为 1。如果都为 1， 说明最终两人的图都是连通的，返回删除了多少边；否则，说明至少一人的图不连通，返回-1.

代码

先分享通用的并查集的模板。来自负雪明烛的博客「代码模板，刷题必会」，地址 https://fuxuemingzhu.blog.csdn.net/article/details/101900729

class DSU:
    def __init__(self):
        self.par = range(10001)
​
    def find(self, x):
        if x != self.par[x]:
            self.par[x] = self.find(self.par[x])
        return self.par[x]

    def union(self, x, y):
        self.par[self.find(x)] = self.find(y)

    def same(self, x, y):
        return self.find(x) == self.find(y)

对于本题而言，需要改造 union() 函数：如果此边属于同一个区域，那么应该删除此边，返回 1；如果此边属于不同的区域，则此边成功连通了两个区域，返回 0。这样，我们就可以直接对 union() 函数的返回结果求和，统计最终删除了多少条边。

本题的 Python 代码如下：

class Solution(object):
    def maxNumEdgesToRemove(self, n, edges):
        A = DSU(n)
        B = DSU(n)
        res = 0
        for edge in edges:
            if edge[0] != 3:
                continue
            res += A.union(edge[1], edge[2])
            # 这里的结果只用加1次，因为只是1条边
            B.union(edge[1], edge[2])
        for edge in edges:
            if edge[0] == 3:
                continue
            cur = A if edge[0] == 1 else B
            res += cur.union(edge[1], edge[2])
        return res if (A.regions() == 1 and B.regions() == 1) else -1

class DSU():
    def __init__(self, n):
        self.par_ = range(n + 1)
        self.regions_ = n
​
    def find(self, x):
        if x != self.par_[x]:
            self.par_[x] = self.find(self.par_[x])
        return self.par_[x]

    def union(self, x, y):
        px = self.find(x)
        py = self.find(y)
        if px == py:
            return 1
        self.par_[px] = py
        self.regions_ -= 1
        return 0

    def regions(self):
        return self.regions_

参考资料：

1. 力扣（LeetCode），https://leetcode-cn.com/problems/remove-max-number-of-edges-to-keep-graph-fully-traversable

2. 花花酱：https://www.bilibili.com/video/BV1PZ4y1N78t

欢迎加入组织

算法每日一题是个互相帮助、互相监督的力扣打卡网站，其地址是 https://www.ojeveryday.com/

想加入千人刷题群的朋友，可以复制上面的链接到浏览器，然后在左侧点击“加入组织”，提交力扣个人主页，即可进入刷题群。期待你早日加入。

公众号：每日算法题

日期

2021 年 1 月 27 日 —— 日更公众号的第3天